1.3.8. Вибір поперечних розмірів хвилеводу, працюючого із

хвилею основного типу

Основними вимогами, яким повинні відповідати хвилеводи, є:

- максимальна потужність, яка передається при мінімальних розмірах поперечного перерізу;

- простота збудження;

- стійкість площини поляризації.

Перші дві вимоги задовольняє хвиля Н₁₀. Дійсно, згідно з формулою (43) тим більше, чим більше значення _кр. Найбільшим значенням _кр характеризується хвиля Н₁₀. Ця ж хвиля має простішу структуру і тому для її збудження можуть бути вико-ристані найпростіші засоби. Однак, якщо розмір b = a або b > a, то площина поляризації хвилі може повернутися на 90. При цьому хвиля Н₁₀ перетворюється у хвилю Н₀₁. Цього допускати не можна. Тому при збудженні хвилі Н₁₀ робоча довжина хвилі джерела повинна задовільняти умові  > _кр (Н₀₁), тобто  > 2b. Звідси виходить, що вертикальний розмір хвилеводу повинен вибиратися із умови 0 < b < /2. Як правило, вибирають b ~ 0.45. Неприпустиме також збудження хвилі Н₂₀. Тому робоча довжина хвилі повинна задовільняти другу умову _кр (Н₂₀) <  < _кр (Н₁₀), якій можна надати вигляду: a <  < 2а. Із цих нерівностей випливає обмеження на вибір горизонтального розміру /2 < a <  . Як правило, а = 0.9.

Таким чином, стійкість площини поляризації гарантується при виконанні нерівності a > b.

1.3.9. Спеціальні види хвилеводів

Розмір широкої стінки хвилеводу можна суттєво зменшити, якщо в порожнині хвилеводу розмістити діелектричну пластинку товщиною d (рис. 4.21). При цьому зменшиться і довжина хвилі у хвилеводі. Так, для випадку d = a довжина хвилі може бути визна-чена співвідношенням

,

де – відносна діелектрична проникність матеріалу пластинки.

Зменшення розміру a супроводжується і зменшенням розміру b. Критична довжина хвилі для поля типу Н₁₀ суттєво зменшується при d/a0,1. Подальше збільшення відносної товщини діелектрика на зменшення _кр(Н₁₀) практично не впливає. Водночас при малих значеннях d/a величина _кр (Н₂₀) практично не змінюється. Тому діелектрична пластина, яка розміщена в центрі хвилеводу, забез-печує розширення смуги, в якій може поширюватись тільки хвиля Н₁₀. Якщо по краях хвилеводу симетрично розмістити дві діелектричні пластини, то смуга робочих частот буде зменшена.

Поряд із хвилеводами прямокутного поперечного перерізу в техніці НВЧ використовують хвилеводи більш складної форми, наприклад, П-подібні (рис. 22) та Н-подібні (рис. 23). Засто-сування таких хвилеводів супроводжується розширенням смуги частот приблизно в п’ять разів. Їхній характеристичний опір нижчий за опір прямокутних хвилеводів.

Очевидно, що такі хвилеводи більш громіздкі, ніж звичайні, тому можуть застосовуватись лише у випадках, коли на габарити системи особливих вимог не накладається.

1.4. Хвилеводи з поперечним перерізом круглої форми

Поряд з прямокутними хвилеводами широко використовуються хвилеводи з поперечним перерізом круглої форми. В них також збуджуються хвилі типів і , але суть індексів m і n тут інша. При дослідженні круглих хвилеводів використовується циліндрична система координат, в якій положення досліджуваної точки задається радіусом r, кутом місця  і відстанню z. Індекс m в цьому випадку характеризує кількість цілих стоячих хвиль, які вміщуються на довжині кола поперечного перерізу радіусом R. Індекс n визначається кількістю максимальних значень напруженості поля вздовж радіуса поперечного перерізу R. Математичний аналіз розповсюдження хвиль в круглих хвилеводах значно складніший, ніж аналіз поля в прямокутних хвилеводах, оскільки здійснюється із застосуванням функцій Бесселя. Однак фізична суть процесів у хвилеводах практично не залежить від форми їхніх поперечних перерізів. Тому для дослідження структури поля в круглому хвилеводі використовуємо викладену раніше методику.

H₁₀

a) б)

Рис. 24

H₁₁

Уявимо собі, що хвилевод круглого перерізу отримано внаслідок деформації стінок хвилеводу прямокутного перерізу. На рис. 24 проілюстровано таке перетворення і показано відповідність хвилі Н₁₀ в прямокутному хвилеводі (рис. 24,а), хвилі в круглому хвилеводі (рис. 24,б). Вектори (суцільні лінії) хвилі мають форму дуг, оскільки згідно з граничними умо-вами підходять до стінок хвилеводу по нормалі. Вектори (пунктирні лі-нії) при цьому по-винні залишатись перпендикулярними векторам в будь-якій точці. Форма силових ліній при цьому також змінюється відповідно до умови перпендикулярності линиям .

а) б)

Рис. 25

Для прикладу розглянемо перетворення хвилі Н₃₁ у прямокутному хвилеводі (рис. 25,а) у відповідну хвилю у хвилеводі круглого перерізу (рис. 25,б). Для спрощення рисунка і полегшення сприйняття хви-левод зображуємо у вигляді з торця, вважаючи неважкою побудову об’ємної структури згідно з принципом її періо-дичності. Тут враховано зміст індексів m та n, граничні умови для елект-ричной та магнітной скла-дових, а також взаємну перпендикулярність силових ліній електричного та магнітного полів у складі структури хвилі.

Для побудови структури поля в круглому хвилеводі необхідно:

- на початковому прямо­кутному хвилеводі із збудженою в ньому хвилею відмітити характерні точки, які визначають положення уявно введених провідних поверхонь;

- перенести ці точки на круглий хвилевод, розбивши його на елементарні хвилеводи нестандартної форми;

- зобразити відповідні лінії векторів і ;

- підрахувати кількість цілих півхвиль на півколі або хвиль на колі поперечного перерізу і визначити значення індексу m (в розглянутому випадку m = 3);

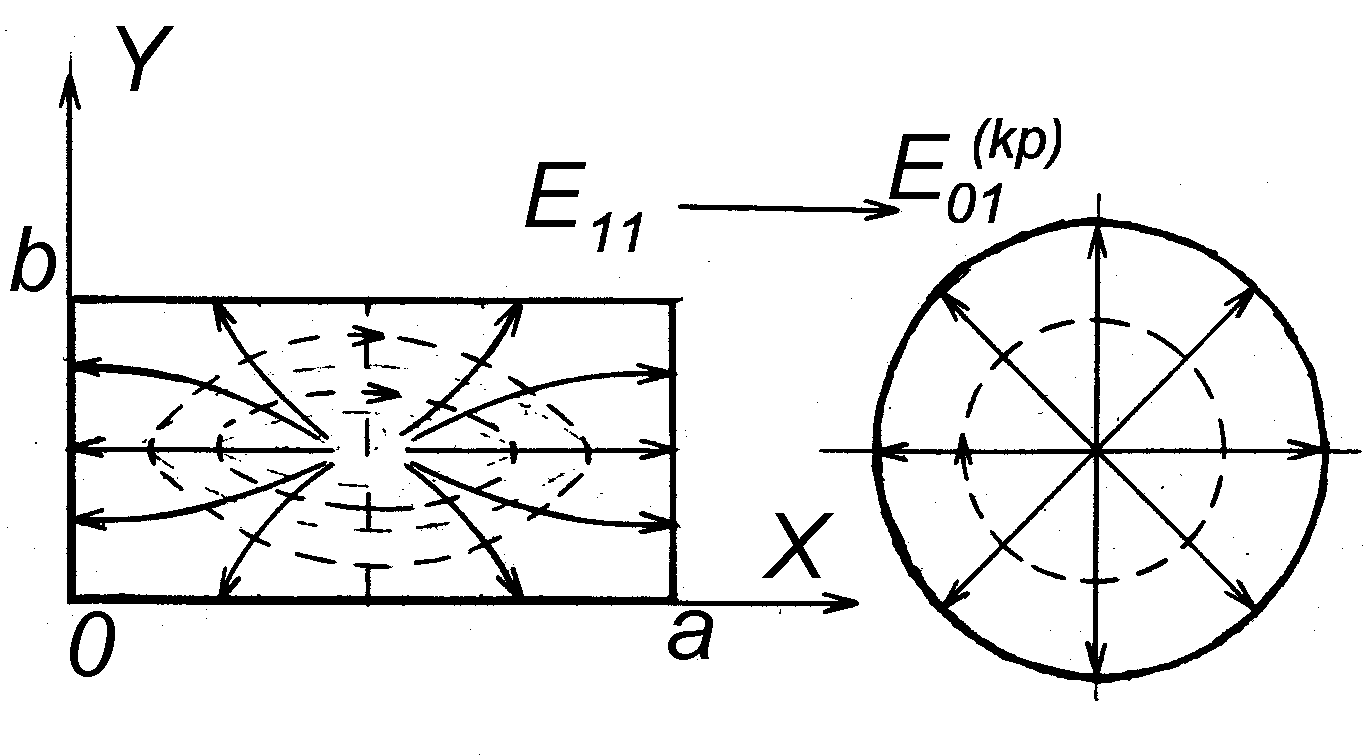
- підрахувати кількість максимумів напруженості поля вздовж радіуса поперечного перерізу і визначити значення індексу n (в розглянутому випадку n = 1). На рис. 26, а, б показана взаємна відповідність хвиль типів і . Слід відмітити, що хвиля характеризується осьовою симетрією і тому застосовується у хвилеводних трактах з обертальними зчленуваннями.

E₁₁

E₁₁^(кр)

а) б)

Рис. 26

Можна сказати, що будь-яка хвиля, що збуджується в прямокутному хвилеводі, має аналог у круглому хвилеводі. Однак зворотне твердження було б несправедливим. В круглому хвилеводі може існувати особлива хвиля , яка не має аналога в прямокутному хвилеводі. Структура поля такої хвилі зображена на рис. 27. Звернемо увагу на такі обставини: вектор має вихровий характер, як і лінії ; лінії струмів зміщення (рис. 28) пронизують площини, які обмежені векторами біля стінок, як наслідок граничних умов, і вони мають тільки поздовжні складові. Відповідні векторам лінії струмів провідності виявляються попе­речними і самозамкненими. Хвиля єдина серед хвиль всіх типів, при якій в стінках хвилеводу немає поздовжніх струмів. Звідси випливає такий важ-ливий висновок: якщо круглий хвилевід із хвилею перерізати поперечною щілиною, то вона буде невипромінюючою і хвиля в ньому поширюється без втрат на випромінювання; в той же час інші типи хвиль, які можуть з’явитися, як перешкоди, будуть знач-но послаблені. Тому такий хвилевод має назву "самофільтруючий". Крім того, зі збільшенням частоти загасання хвилі моно-тонно зменшується, оскільки при її розповсюдженні вихрові струми Фуко відсутні. Тому круглий хвилевід із хвилею застосо-вують для передачі енергії на порівняно великі відстані.

Рис. 27 Рис. 28

Рис. 29

Розподіл критичних довжин хвиль для хвилеводів круглого по-перечного перерізу радіусом R показано на рис. 29. В розглянутому випадку коефіцієнти при R визначаються від-повідними значеннями функції Бесселя. Із рис. 29 видно, що для хвилеводів круглого перерізу хвилею основного типу є хвиля.