11. Поляризація однорідних плоких хвиль

Припустимо, що фронт однорідної плоскої хвилі розташований у площині і векторз віссюскладає кут поляризації. Площа, в якій розташовані вектор напруженості електричного поля та вектор Умова-Пойнтінга, називається площиною поляризації (рис. 5).

Необхідно з’ясувати, як поводить себе вектор з часом та в просторі при зміні співвідношень між його проєкціямита. Для хвилі, утвореної змінним струмом, значеннязмінюється з часом за гармонічним законом:

,

де та– амплітудні значеннята. Розглянемо часткові випадки цього відношення.

1. Нехай початкові фази . Тоді модуль вектора:

залежить від часу, а кут поляризації:

від часу не залежить, і така поляризація називається лінійною.

2. Нехай . Тоді

,

тобто модуль вектора :

від часу не залежить, а кут поляризації:

залежить від часу. Кінець результуючого вектора при цьому описує коло, і поляризація називається круговою.

3. Нехай ,. При цьому модуль вектората кут поляризаціїє функціями часу. Така поляризація називається еліптичною.

Таким чином, назва виду поляризації відповідає геометричній фігурі, яка описується в часі кінцем вектора в площині. Електромагнітні хвилі завжди поширюються в конкретному середовищі. Вище, розглядаючи класифікацію середовищ за провідністю, ми з’ясували, що одне і те ж середовище для хвилі однієї частоти може бути провідним, а для хвилі іншої частоти – діелектричним. Одержимо тепер співвідношення для кількісної оцінки параметрів, що характеризують поширення хвиль в різних середовищах.

12. Хвильові рівняння для однорідних плоских хвиль

Припустимо що в просторі відсутні заряди, тобто . При цьому хвильове рівняння (29) для вектораспрощується:

. (31)

Оскільки вектор заданий сумою проекцій, то рівнянню (31) відповідає система трьох рівнянь:

(32)

Використовуючи ознаки однорідних плоских хвиль, систему (32) запишемо у вигляді:

(33)

Аналогічним чином змінимо хвильове (30) рівняння відносно складових вектора :

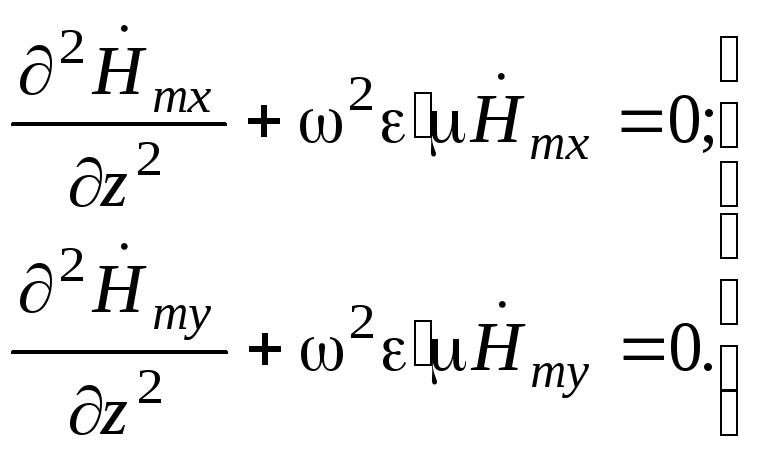(34)

Рівняння (33) та (34) мають однакову структуру і однакові загальні розв’язки. Це однорідні диференційні рівняння другого порядку. Їх елементи – комплексні амплітуди – містять показникові функції. Тому загальні розв’язки хвильових рівнянь доцільно виразити також через показникові функції. Отже перед другим доданком рівнянь (33) і (34) необхідно знак "плюс" змінити на "мінус". Позначимо , тоді:

. (35)

Рівняння (33) та (34) набудуть вигляду:

(36)

(37)

(38)

(39)

Розв’язки цих рівнянь визначають проекції векторів тав будь-якій точці осів будь-який момент часу. Якщо серед рівнянь (36) – (39) будуть взаємозв’язані пари, то тоді можна розв’язувати тільки два рівняння. Зв’язок між векторами тавстановлюється першим та другим рівнянням Максвела. Використаємо перше:

.

Враховуючи те, що вектори тазадаються геометричною сумою своїх проекцій, та використовуючи запис ротора в декартовій системі координат, запишемо перше рівняння Максвела у вигляді сукупності трьох скалярних рівнянь:

(40)

Враховуючи ознаки однорідних плоских хвиль, спростимо вирази (39):

(41)

Отже, проекція зв’язана з , а рівняння (36), (39) та (41) характеризують горизонтально-поляризовану хвилю. Рівняння (36) – (38) описують скісно-поляризовану хвилю.