17. Елементарний електричний вібратор

Елементарний електричний вібратор (диполь Герца) – це короткий в порівнянні з довжиною хвилі відрізок провідника довжиною, по якому тече електричний струм. Для нього слушні такі обмеження:

– відстань від точки спостереження до будь-якої точки є величина незмінна;

– розподілення струму по довжині вібратора – рівномірне;

– фаза струму, який тече по вібратору, в кожній його точці в будь-який момент часу одна й та ж.

Нехай електричний вібратор розміщений відносно початку координат так, як показано на рис. 8.

Напруженість поля, котре він збуджує в будь-якій точці простору, може бути визначена з такого алгоритму:

• за густиною струму 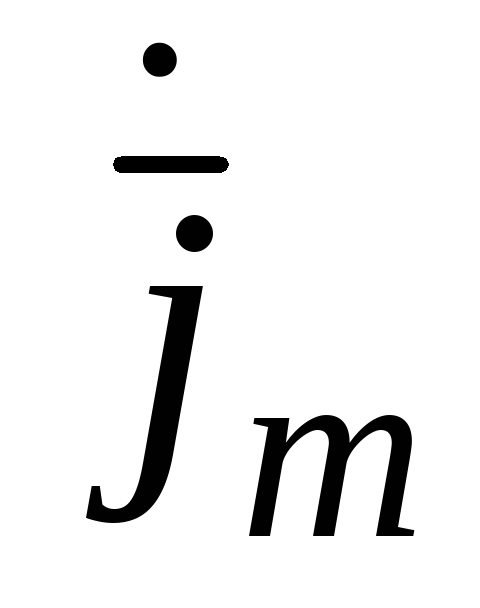, який тече по вібратору, на основі

виразу (3.62) можна знайти ;

– за потенціалом у відповідності з рівнянням (58) знайдемов будь-якій точці простору;

- використовуючи перше рівняння Максвела за відомим , визначимо напруженість.

Припустимо, що оточуючий простір – безмірний ідеальний діелектрик, в якому відсутні струми провідності та заряди. Згадаємо, що густина стороннього струму у диполі, та відповідний йому векторний потенціалпаралельні. Оскількиспівпадає з віссю(рис. 3.8), то вектормає лише одну проекцію:

(73)

Враховуючи, що об’єм елемента диполя , де– площина поперечного перетину, а, (72) спрощується:

, (74)

де – комплексна амплітуда струму вібратора.

При обмеженнях, які сформульовані вище, підінтегральна функція співвідношення (74) для будь-якої точки вібратора постійна. Тому

.

Електричний вібратор досліджуємо в сферичній системі координат . Тоді, як випливає з рис. 3.8, для складових векторного магнітного потенціалу отримаємо :

; (75)

;

. (76)

Визначимо тепер проекції вектора . У відповідності з рівнянням (58):

.

В сферичній системі координат це співвідношення набуває такого вигляду:

Оскільки обидві частини записані відносно одних і тих же проекцій, з обліком відношень (3.75) та (3.76), одержимо:

; (77)

; (78)

. (79)

Отже, магнітне поле електричного вібратора має лише азимутальну складову .

Знайдемо тепер складові електричного поля. Для цього скористуємося першим рівнянням Максвела в комплексному вигляді з урахуванням того, що для ідеального діелектрика = 0:

.

З цього рівняння випливає, що

.

Якщо подати обидві частини цього відношення через проекції, то одержимо:

Якщо підставити в одержане відношення відповідні значення проекцій вектора (77) – (79), то після диференціювання отримаємо:

; (80)

; (81)

. (82)

Таким чином, складові вектора розташовуються в площинах, які перпендикулярні векторунезалежно від кута. Кожна складова поля має декілька компонентів. Одні компоненти синфазні з струмом, інші - зсунуті відносно нього за фазою на 90^О. В залежності від відстані одні компоненти зменшуються швидше, інші повільніше. В зв’язку з цим простір, що оточує вібратор, можна умовно розділити по геометричній ознаці на зони, в кожній з яких поле має специфічні особливості. Область простору, яка обмежена значеннями , називають ближньою зоною вібратора; область простору, яка обмежена значеннями, називають дальньою зоною; область простору, для якоїназивають проміжною зоною.

Розглянемо особливості електромагнітного поля вібратора в кожній зоні і одержимо відповідні аналітичні співвідношення.