Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Vischa_matematika_Chastina_3_Denisyuk_Repeta

.pdf

Скачиваний:

516

Добавлен:

19.02.2016

Размер:

7.52 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 459 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Аналогічно,	помноживши рівність (1.25) на sin kx і проінтегрувавши
почленно на відрізку [−π; π]				утворений ряд, дістанемо

					1	π
		bn		=		∫ f (x) sin nxdx.	(1.33)
					π
						−π

Числа a0 ,	an , bn , які визначаються формулами (1.31) – (1.33), назива-
ють коефіцієнтами Фур’є функції f (x) , а тригонометричний ряд (1.25),
коефіцієнтами якого є коефіцієнти Фур’є функції f (x) , називають рядом
Фур’є функції	f (x) .

Для інтегровної на відрізку [−π; π] функції f (x) пишуть:
			a0			∞
	f (x) ~				+ ∑ (an cos nx + bn sin nx) .		(1.34)

				2		n=1
Знак відповідності (~) означає, що інтегровній на відрізку [−π; π]							фун-

кції f (x) поставлено у відповідність її ряд Фур’є.

З’ясуємо умови, за яких знак відповідності у формулі (1.34) можна замінити знаком рівності, тобто умови, за яких ряд Фур’є збігається і має

своєю сумою функцію f (x) .

Сформулюємо теорему, яка дає достатні умови подання функції f (x) через її ряд Фур’є.

	(Діріхле). Нехай 2π — періодична функція f (x) на відрізку
Теорема
	[−π; π] задовольняє умови (Діріхле):

1)f (x) кусково-неперервна, тобто неперервна або має скінченне число точок розриву першого роду;

2)f (x) кусково-монотонна, тобто монотонна на всьому відрізку або

цей відрізок можна розбити на скінченне число інтервалів так, що на кожному з них функція монотонна.

Тоді ряд Фур’є функції f (x) є збіжним на всій числовій прямій і сума S(x) ряду Фур’є задовольняє рівності:

1) у точках неперервності функції f (x) S(x) = f (x), тобто

	a0	∞
f (x) =		+ ∑ (an cos nx + bn sin nx) ;

2		n=1

http://vk.com/studentu_tk, http://studentu.tk/

2) якщо x0 ― точка розриву (першого роду) функції f (x) , то

S(x0 ) =	f (x0	− 0) + f (x0	+ 0)	,
S(x0 ) =		2		,
		2

тобто сума ряду Фур’є в точці розриву x0 дорівнює середньому арифметичному односторонніх границь функції f (x) у цій точці;

3) в кінцевих точках x = −π, x = π відрізка [−π; π] сума ряду Фур’є

набуває значень

S(−π) = S(π) = f (−π + 0) + f (π − 0) . 2

Зауваження.

1. Для довільної інтегровної 2π -періодичної функції ϕ(x) виконується рівність

πa+ 2π

∫ ϕ(x)dx = ∫ ϕ(x)dx .

−π

Тому коефіцієнти Фур’є можна обчислювати за формулами

1 a+ 2π

∫

f (x)dx , a

∫

f (x) cos nxdx ,

1 a+ 2π

b =

∫

f (x) sin nxdx,

де a ― довільне дійсне число.

2. Якщо функція

f (x)

розкладається в ряд Фур’є, то частинні суми Sn (x)

цьогоряду(многочлениФур’є) даютьзмогузнайтинаближення цієїфункції

								a0	n
					f (x) ≈ Sn (x) =			a0	+ ∑ (ak cos kx + bk sin kx).
					f (x) ≈ Sn (x) =				+ ∑ (ak cos kx + bk sin kx).
							2		k =1
Похибка цієї формули зменшується із збільшенням числа n .
3. Оскільки an cos nx + bn sin nx = An sin(nx + ϕn ) , торядФур’єфункції f (x)
можна подати у вигляді
									∞
							f (x) = A0 + ∑ An sin(nx + ϕn ).
									n=1
Числа ωn					= 0, 1,	2, ..., утворюють дискретний спектр функції f (x) ; чис-
ла A	0	=	a0	,	A =	a2	+ b2 ( n = 1,		2, 3, ... ) ― амплітудний спектр, а числа
ла A		=		,	A =	a2	+ b2 ( n = 1,		2, 3, ... ) ― амплітудний спектр, а числа
		2			n	n	n
		2
82

http://vk.com/studentu_tk, http://studentu.tk/

ϕn = arctg	an	( n = 1, 2, 3, .... )	― фазовий спектр функції f (x) . Період

	bn		в акустиці називають основним тоном, він
першої гармоніки A1 sin(x + ϕ1 )
збігається з періодом функції			f (x) . Частоти решти гармонік, що назива-

ють обертонами і створюють тембр звуку, кратні основній частоті. 4. При обчисленні коефіцієнтів Фур’є корисно пам’ятати формули

sin nπ = 0 , cos nπ = (−1)n , n = 0, 1, 2, ... .

3.3. Ряд Фур’є для парних і непарних функцій

Обчислення коефіцієнтів ряду Фур’є спрощується, якщо функція f (x)

є парною або непарною. При цьому вигляд ряду Фур’є також спрощується, він стає неповним (див. табл.3).

										Таблиця 3

Властивість функції f (x)	f (x) — парна функція							f (x) — непарна функція

		a0			∞				∞
Ряд Фур’є		a0	+ ∑an cos nx						∑bn sin nx
Ряд Фур’є	2		+ ∑an cos nx						∑bn sin nx
	2			n=1					n=1

	b = 0, a =					2	π f (x)dx ,	a0 = 0, an = 0,
	b = 0, a =						π f (x)dx ,	a0 = 0, an = 0,
	n				0	π ∫
	n				0
Коефіцієнти Фур’є						0			2 π
				π				bn =		f (x)sin nxdx
								bn =		f (x)sin nxdx
				∫					π ∫0
	an =		π	∫	f (x)cos nxdx
	an =		2		f (x)cos nxdx
				0

3.4. Ряд Фур’є для 2l- періодичних функцій

Розкладати в ряд Фур’є можна також періодичні функції з періодом, відмінним від 2π .

Нехай функція f (x) визначена на відрізку [−l; l], має період 2l ( l ― довільне додатне число) і задовольняє на цьому відрізку умови Діріхле.

У цьому разі ряд Фур’є функції				f (x) має вигляд

		a0	∞		πnx			πnx
	f (x) =		+ ∑	an cos	l	+ bn	sin	l	,	(1.35)
	f (x) =	2	+ ∑	an cos		+ bn	sin		,	(1.35)
		2	n 1
			=
де коефіцієнти Фур’є визначають за формулами
										83

http://vk.com/studentu_tk, http://studentu.tk/

1 l

πnx

a =

∫

f (x)dx,

a =

∫

f (x) cos

dx,

−l

(1.36)

1 l

πnx

b =

∫

f (x) sin

dx.

−l

Формули (1.35), (1.36) можна дістати з формул (1.25), (1.31)—(1.33) для

функції ϕ(t), пов’язаної з функцією f (x)				формулами:
x =	lt	, ϕ(t) = f	lt	, t [−π; π].
	π	π

Зауваження. Усі теореми, які справджуються для рядів Фур’є 2π -пе- ріодичних функцій, зберігаються і для рядів Фур’є 2l-періодичних

функцій.

Для парних і непарних функцій, заданих на відрізку [−l; l], вигляд ряду Фур’є та формули для обчислення його коефіцієнтів вміщені у табл. 4.

Таблиця 4

Властивість функції f (x)

f (x) — парна функція

f (x) — непарна функція

∞

πnx

∞

πnx

Ряд Фур’є

+ ∑an cos

∑bn sin

n=1

b = 0, a =

l f (x)dx,

a = 0, a = 0,

Коефіцієнти Фур’є

∫

πnx

l f (x)cos

∫ f (x)sin

πnx dx

bn =

an =

l ∫

3.5. Ряди Фур’є для функцій, заданих на відрізку [0; l] або на довільному відрізку [a; b]

Нехай функцію задано на відрізку [0; l] . Довизначимо цю функцію на інтервалі (−l; 0) довільно (зберігаючи виконання умов теореми Діріхле) і продовжимо цю функцію з періодом 2l на всю числову пряму. Утворену

функцію можна розкласти у ряд Фур’є за формулами (1.35), (1.36) багатьма способами, залежно від вибору функції на інтервалі (−l; 0) . Ці розклади

дають ряд Фур’є на всій прямій, отже, і на проміжку [0; l] .

http://vk.com/studentu_tk, http://studentu.tk/

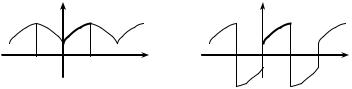
Найважливішими для застосування є такі два випадки:

1. Довизначимо функцію f (x) , задану на відрізку [0; l] , на інтервал (−l; 0) парним чином, тобто f (x) = f (− x) для x (−l; 0) (рис. 1.5, а). Тоді функцію f (x) на проміжку (−l; l) можна вважати парною і її ряд Фур’є містить тільки косинуси (див. формули у табл. 4).

2. Довизначимо тепер функцію f (x) на інтервал (−l; 0) непарним чи-

ном, тобто f (x) = − f (− x) для		x (−l; 0) (рис. 1.5, б). Тоді функцію f (x)
на проміжку (−l; l)	можна вважати непарною і її ряд Фур’є містить тільки
синуси (табл. 4).
y у = f (x)			y у = f (x)
–l O	l	x	–l O	l	x
a		б
		Рис. 1.5
Нехай кусково-монотонну функцію f (x)			задано на відрізку [a; b], де

a < b. Розглянемо періодичне продовження заданої функції на всю числову

пряму з періодом

T = b − a,

тобто

утворимо

функцію f1 (x) таку, що

f1 (x) = f (x) для x (a; b)

f1 (x + T ) = f1 (x) .

Позначимо 2l = T = b − a,

тобто l =

b − a

. Оскільки функція f (x)

задовольняє рівності

a+ 2l

∫ f1 (x)dx = ∫ f1 (x)dx = ∫ f (x)dx ,

то маємо

−l

∞

πnx

(x) ~

+ ∑

cos

+ bn

sin

n=1

де коефіцієнти Фур’є визначають за формулами

1 b

πnx

∫

f (x)dx,

∫

f (x) cos

dx,

(1.37)

1 b

πnx

b − a

∫

f (x) sin

dx ( l =

http://vk.com/studentu_tk, http://studentu.tk/

Враховуючи, що f1 (x) = f (x) для x (a; b) , то в точках неперервності відрізка [a; b] сума ряду Фур’є дорівнює f (x).

Звичайно, функцію f (x) , задану на довільному скінченному відрізку [a; b] , можна розкласти у ряд Фур’є й іншими способами.

3.6. Комплексна форма ряду Фур’є

Ряди Фур’є часто застосовують у комплексній формі. Використовуючи формули Ейлера

cos nx =

einx + e−inx

sin nx =

einx − e−inx

ряд Фур’є для 2π -періодичної функції

f (x)

можна подати у вигляді

n=∞

f (x) = ∑ cn einx ,

(1.38)

n=−∞

коефіцієнти якого мають вигляд

(1.39)

cn = ∫

f (x)e−inx dx ( n = 0,

± 1, ± 2, ... ).

−π

Рівність (1.38) називають комплексною формою ряду Фур’є функції f (x) , а числа cn , які визначаються формулою (1.39), ― комплексними ко-

ефіцієнтами ряду Фур’є.

Т.3 ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ

1. Розкладіть у ряд Фур’є 2π -періодичну функцію

f (x) = −1, ÿêù î	x (0; π),	f (x + 2π) =
2, ÿêù î	x [−π; 0],

Побудуйте графік суми ряду Фур’є.

	f(x)
	2
–π	О	π	х	–π
	–1

f (x) (рис. 1.6, a).

S(x)
2	0,5
	0,5
О	π	х
–1

Рис. 1.6

http://vk.com/studentu_tk, http://studentu.tk/

Розв’язання. Задана функція задовольняє умови теореми Діріхле, тому її можна розкласти в ряд Фур’є. Обчислимо коефіцієнти Фур’є за форму-

лами (1.31) — (1.33). Маємо

∫

f (x)dx =

∫

(−1)dx +

∫

− x

+ 2x

π −π

2dx

= 1;

π − π

−π

∫

f (x) cos nxdx

∫

− cos nxdx +

∫

2 cos nxdx

− π

−π

sin nx

2 sin nx

−

= 0;

−π

1 cos nx

bn =

∫

f (x) sin nxdx =

∫

− sin nxdx +

∫

−

2 sin nxdx =

− π

−π

2 cos nx

3(1− (−1)

)

−

(cos 0

− cos(−π) − 2 cos π + 2 cos 0) =

πn

Підставивши значення коефіцієнтів a0 , an ,

у формулу (1.25), діста-

немо

∞

)

f (x) =

∑

3(1− (−1)

sin nx.

Оскільки

n=1

πn

якщо n = 2k,

bn =

, якщо n = 2k − 1,

π(2k − 1)

то розвинення у ряд Фур’є набуває вигляду

∞

sin(2k − 1)x

f (x) =

∑

π k =1

2k − 1

Ця рівність виконується для всіх точок неперервності заданої функції,

тобто для x ≠ πn , n Z . У точках x = πn сума ряду дорівнює					півсумі
односторонніх границь у цих точках, тобто S(πn) =	−1+ 2	=	1	.	Графік
	2
суми ряду Фур’є зображено на рис. 1.6, б.		2

Зауваження. Якщо f (x) = g(x) + C, де g(x) ― непарна 2π -періодич-
нафункція, аC ― стала, то ряд Фур’є для функції	f (x)	має вигляд
					87

http://vk.com/studentu_tk, http://studentu.tk/

∞

f (x) = C + ∑bn sin nx.

n=1

Обґрунтуйте це самостійно.

2. Розкладіть у ряд Фур’є 2π -періодичну функцію

f (x) = 0, якщо x (−π; 0),	f (x + 2π) = f (x) (рис. 1.7).
x, якщо x [0; π],

Розв’язання. Задана функція є кусково-монотонною, тому її можна розкласти в ряд Фур’є. Знаходимо коефіцієнти Фур’є функції f (x) :

1 x2

a0 =

∫

0 dx +

∫

;

xdx

π 2

−π

∫

0 cos nxdx +

∫

x cos nxdx =

x cos nxdx

π 0

−π

u = x,

dv = cos nxdx

sin nx

π sin nx

sin nx

−

∫

du = dx,

v =

(−1)n − 1

cos nx

;

πn2

∫

sin nxdx +

∫

x sin nxdx =

x sin nxdx

π 0

−π

u = x,

dv = sin nxdx

cos nx

π cos nx

∫

= dx,

v = −

cos nx

− x

(−1)n+1

sin nx

(−1)n+1

πn

Отже, ряд Фур’є для заданої функції має вигляд

∞

(−1)

− 1

(−1)

n+1

f (x) =

π + ∑

cos nx +

sin nx ,

πn2

або

n=1

f (x) =

cos x

cos 3x

cos 5x

sin x

sin 2x

sin 3x

−

+ …

−

− … .

π 1

http://vk.com/studentu_tk, http://studentu.tk/

В усіх точках, крім x = −π + 2πk, k Z , сума ряду дорівнює значенню функції f (x) . У точках x = −π + 2πk, k Z сума ряду дорівнює π2 .

Оскільки x = 0 — точка неперервності функції f (x), то справджується

рівність
		f (0) =			π			2			1						1				1
							−								+				+				+ …		,
					4		−						2		+		2		+	5		2	+ …		,
					4				π			1			3					5
але за умовою f (0) = 0, отже,
				π			2 1								1				1
0 =					−									+				+				+ … ,
0 =				4	−						2			+		2		+	5	2		+ … ,
				4			π			1					3				5
звідси

		1	+	1		+		1			+ …+						1		+ …=					π2	.
	12		+	32		+	52				+ …+						n2		+ …=					8	.
	12			32			52										n2							8

Висновок. За допомогою рядів Фур’є можна знаходити суми числових рядів.

3. Розкладіть у ряд Фур’є 2π -періодичну функцію

f (x) = | x |, f (x + 2π) = f (x) (рис. 1.8).

Розв’язання. Задана функція задовольняє умови Діріхле, парна, тому ряд Фур’є для цієї функції має вигляд

∞

f (x) =

+ ∑ an cos nx .

n=1

Знайдемо коефіцієнти Фур’є a0 та an (див. табл. 3):

2 π

xdx =

2 x2

= π;

π ∫

π 2

sin nx

π sin nx

∫

x cos nxdx =

−

∫

2 cos nx

((−1)n − 1).

πn2

http://vk.com/studentu_tk, http://studentu.tk/

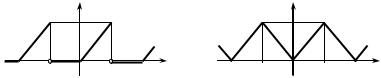
Отже, ряд Фур’є для заданої функції має вигляд

∞

(−1)

−

∞

cos(2k − 1)x

f (x) =

∑

cos nx =

−

∑

(2k − 1)2

π n=1

π k =1

(1.40)

cos x

cos 3x

cos 5x

−

+ … .

Оскільки задана функція f (x) неперервна на всій числовій прямій, то формула (1.40) справджується для будь-якого x R .

у	у
π	π

–2π –π О

2π х

–2π –π О

2π х

Рис. 1.7 Рис. 1.8

4. Розкладіть у ряд Фур’є за синусами функцію f (x) = x2 , x [0; π]. Розв’язання. Продовжимо функцію f (x) непарним способом на про-

міжок [−π; 0) , а потім продовжимо періодично з періодом 2π на всю чис-

лову пряму

(рис.

1.9).

На

відрізку

[−π; π]

функція

непарна, і тому

a0 = an = 0 . Коефіцієнт bn знайдемо за формулою bn =

∫ f (x)sin nxdx .

Маємо

− cos nx

sin nxdx =

x cos nxdx

∫0

cos nπ

sin nx

−π

−

∫ sin nxdx =

π2

n+1

2π

n+1

n (−1)

cos nx

(−1)

− 1 .

πn3

Отже,

∞

2π

∞

f (x) = ∑

(−1)n+1 sin nx + ∑

(−1)n − 1 sin nx .

n=1

πn3

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 459 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2019882.69 Кб44Vikova_psikhol_Konsp_Alp.doc
#
19.02.2016908.69 Кб58Vischa_geodeziya.docx
#
19.02.20168.29 Mб325Vischa_matematika_Chastina_1_Denisyuk_Repeta.pdf
#
19.02.20164.86 Mб979Vischa_matematika_Chastina_2_Denisyuk_Repeta.pdf
#
19.02.20162.32 Mб226Vischa_matematika_Chastina_2_Denisyuk_Repeta.pdf
#
19.02.20167.52 Mб516Vischa_matematika_Chastina_3_Denisyuk_Repeta.pdf
#
19.02.20161.68 Mб81Vitorskaya_N_Prichiny_Bolezn_Istoki_Zdorov_Pra.doc
#
06.12.2019847.52 Кб0Vizio.docx
#
26.08.201978.26 Кб0voprosy_1-10.docx
#
19.02.201650.69 Кб79Voprosy_na_ekzamen_TS.doc
#
26.12.201951.91 Mб0VP_Ger_Rakh_dlya_tip_posl.doc