
Vischa_matematika_Chastina_3_Denisyuk_Repeta
.pdf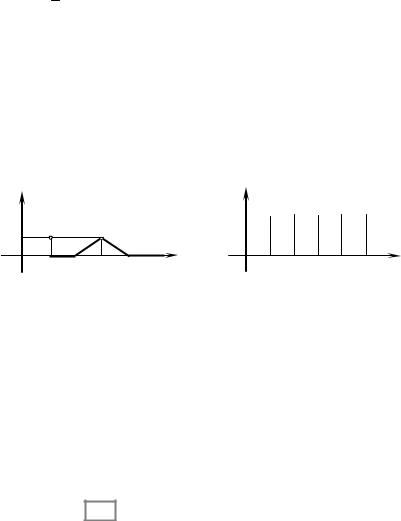
+ 1 |
− |
t − 3a |
− |
t − 2a |
|
η(t − 3a) − 1 |
− |
t − 3a |
|
η(t − 4a) = η(t) − η(t − a) + |
|
a |
a |
a |
|||||||||
|
|
|
|
|
|
|
|
+ 1a ((t − 2a)η(t − 2a) − 2(t − 3a)η(t − 3a) + (t − 4a)η(t − 4a)).
Користуючись властивостями 20 і 40, дістанемо шукане зображення
|
1 |
|
1 |
|
−ap |
|
1 |
|
1 |
|
−2ap |
|
2 |
|
−3ap |
|
1 |
|
−4ap |
|
|||
F( p) = |
|
− |
|
e |
|
+ |
|
|
|
|
e |
|
− |
|
|
e |
|
+ |
|
|
e |
|
. |
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|||||||||||
|
p |
|
p |
|
|
|
a |
|
p |
|
|
|
p |
|
|
|
p |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
17. Знайдіть зображення прямокутного періодичного імпульсу з періодом 2b (рис. 4.9).
|
|
|
A |
для |
0 < t ≤ b, |
|
||||||||||
|
|
f (t) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
для b< t ≤ 2b. |
|
|||||||||||
f(t) |
|
|
|
|
f(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
О |
а 2а 3а 4а |
t |
|
О |
|
|
|
|
|
|
|
|
|
|
||
|
b 2 |
b 3 |
b 4 |
b 5 |
b |
|||||||||||
|
Рис. 4.8 |
|
|
|
|
|
|
|
Рис. 4.9 |
|
||||||
Розв’язання. Знайдемо зображення функції на проміжку 0 < t ≤ 2b (на одному періоді):
|
b |
|
|
|
|
e |
− pt |
|
b |
A |
|
|
|
F0 ( p) = ∫ Ae− pt dt = A |
|
|
= |
(1 − e− pb ) . |
|||||||||
− p |
|
|
|||||||||||
0 |
|
|
|
|
|
0 |
p |
|
|||||
Тоді за формулою (1.5) дістанемо |
|
|
|
|
|
|
|
||||||
f (t) |
|
1 |
|
A |
(1 − e− pb ) = |
|
|
A |
. |
||||
|
|
|
|
p(1 + e− pb ) |
|||||||||
1 |
− e−2 pb p |
|
|
|
|
|
|||||||
Т.1 ВПРАВИ ДЛЯ АУДИТОРНОЇ
ІСАМОСТІЙНОЇ РОБОТИ
1.Перевірте, які з заданих функцій є функціями-оригіналами:
1) f (t) = bt η(t), b > 0, b ≠ 1. |
2) f (t) = e (2+ 4i)t η(t). |
351
http://vk.com/studentu_tk, http://studentu.tk/
3) |
f (t) = |
1 |
|
η(t). |
4) |
f (t) = t2 η(t). |
||
t − |
3 |
|||||||
|
|
|
6) f (t) = tg t η(t). |
|||||
5) |
f (t) = ch (3 − i)t η(t). |
|||||||
7) |
f (t) = tη(t). |
8) |
f (t) = η(t)e−t cos t. |
|||||
2. Користуючись означенням, знайдіть зображення функцій: |
||||||||
1) f (t) = t. |
|
|
2) f (t) = (t − 1)et . |
|||||
3) |
f (t) = sin 3t. |
4) |
f (t) = t2 . |
|
||||
5) |
f (t) = e2t . |
|
|
6) |
f (t) = (2t − 1)e−t . |
|||
7) f (t) = t et . |
|
|
8) f (t) = tα (α > −1). |
|||||
3. Знайдіть зображення оригіналів: |
|
|
|
|||||
|
|
1, |
|
0 ≤ t < 2, |
|
t, |
0 ≤ t < 2, |
|
1) |
f (t) = |
|
|
|
2) |
|
− t)2 , 2 ≤ t < 4, |
|
−1, 2 ≤ t < 3, |
f (t) = (4 |
|||||||
|
|
|
|
|
|
|
4 ≤ t. |
|
|
|
0, 3 ≤ t. |
|
0, |
||||
4. Користуючись властивостями 20 і 30, знайдіть зображення функцій:
1) |
f (t) = sin2t. |
2) |
f (t) = cos2t. |
3) |
f (t) = cos3t. |
4) |
f (t) = ch ωt. |
5) |
f (t) = sinαt cosβt. |
6) |
f (t) = sinαt sinβt. |
7) |
f (t) = sin4t. |
8) |
f (t) = cos3ωt. |
5. Користуючись властивостями 40 і 50, знайдіть зображення функцій:
1) |
f (t − 1) = (t − 1)2 η(t − 1). |
2) |
f (t − b) = sin(t − b)η(t − b). |
3) |
f (t) = et cos nt. |
4) |
f (t) = e−tt3 . |
6. Користуючись властивістю 60, знайдіть зображення функцій: |
|||
1) |
f (t) = cos2t. |
2) |
f (t) = cos3t. |
3) |
f (t) = cos4 t. |
4) |
f (t) = t sin ωt. |
352
http://vk.com/studentu_tk, http://studentu.tk/

|
|
|
7. Користуючись властивістю 70, знайдіть зображення функцій: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
1) f (t) = t2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) f (t) = tn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
3) |
f (t) = t cos2t. |
|
|
|
|
|
|
|
|
|
|
|
|
4) f (t) = t e−3t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
5) f (t) = t(et + ch t). |
|
|
|
|
|
|
|
|
|
|
|
|
6) f (t) = t2sh t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
8. Користуючись властивістю 80, знайдіть зображення функцій: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
1) f (t) = ∫t |
sin τd τ. |
|
|
|
|
|
|
|
|
|
|
|
|
2) f (t) = ∫t |
(τ + 1)cosτd τ. |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
9. Користуючись властивістю 90, знайдіть зображення функцій: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
1) |
f (t) = |
|
et − 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
f (t) = |
1− e−t |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
10. Користуючись властивістю 100, знайдіть зображення функцій: |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1) |
f (t) = ∫t |
(t − τ)2 cos 2τd τ . |
|
|
|
|
|
|
|
|
2) f (t) = ∫t |
τet−τ sin (t − τ)d τ . |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
11. Знайдіть зображення функцій, заданих графічно (рис.4.10—4.12): |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
f(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
t |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
О |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
2 |
|
|
|
|
О |
|
|
|
|
|
|
|
|
|
|
|
t |
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
Рис. 4.10 |
|
|
|
|
|
|
Рис. 4.11 |
|
|
|
|
|
|
Рис. 4.12 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Відповіді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1. |
|
1) так; |
|
2) так; |
3) ні; 4) так; 5) так; |
6) ні; 7) так; 8) так. |
2. 1) |
1 |
; |
2) |
|
2 − p |
|
; |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
p |
2 |
( p − 1) |
2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3) |
|
|
3 |
|
|
; 4) |
2 |
; 5) |
|
1 |
|
; 6) |
|
1 − p |
|
3. 1) |
1 |
(1 + e−3 p − 2e−2 p ); 2) |
|
|
1 |
|
|
(2 − 2 pe−2 p − |
||||||||||||||||||||||||||
|
|
p2 + 9 |
|
p3 |
|
|
p − 2 |
|
|
( p + 1)2 |
|
p |
|
|
|
|
|
|
|
|
|
|
2 p2 |
|
|
|
|
|
|
|
||||||||||||||||||||
− |
3e |
−2 p |
+ e |
−4 p |
); |
|
4. |
|
1) |
|
|
2 |
|
|
; |
2) |
|
p2 + 2 |
|
; |
3) |
|
|
p3 + 7 p |
|
|
|
|
; |
4) |
|
p |
|
; |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p ( p2 |
+ 4) |
|
|
|
|
|
p( p2 + 4) |
|
( p2 |
+ 9)( p2 |
+ 1) |
|
|
|
|
p2 − ω2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
353 |
||||
http://vk.com/studentu_tk, http://studentu.tk/

|
|
|
|
α( p2 |
+ α2 − β2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2α βp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
p |
|
|
|
4 p |
|
|
|
|
|||||||||||||||||||||
5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
7) |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
− |
|
|
|
|
; |
||||||||
|
|
( p |
2 |
+ α |
2 |
|
+ β |
2 |
) |
2 |
− 4α |
2 |
β |
2 |
|
|
|
|
|
( p |
2 |
+ α |
2 |
+ |
|
β |
2 |
) |
2 |
− 4α |
2 |
β |
2 |
|
|
|
|
|
|
8 |
|
|
p |
|
|
|
|
|
p |
2 |
|
+ 16 |
|
|
|
p |
2 |
+ 1 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
8) |
|
|
ω( p3 + 7 pω) |
|
. |
|
5. 1) |
2e− p |
; 2) |
|
e−b p |
; |
3) |
|
|
|
|
p − 1 |
|
|
|
; |
4) |
|
|
|
6 |
|
|
|
|
|
. 6. 1) |
|
|
|
p2 + 2 |
|
; |
|||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
( p |
|
+ 9ω |
)( p |
|
+ ω ) |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
p |
|
|
+ 1 |
|
|
|
|
|
( p − 1) |
|
|
+ n |
|
|
|
|
|
|
( p + 1) |
|
|
|
|
|
|
|
|
|
p( p |
|
+ 4) |
|
|
|
||||||||||||||||||||||||
2) |
|
|
|
p3 + 7 p |
|
|
|
|
|
; 3) |
|
|
|
p4 + 16 p2 + 24 |
; |
|
4) |
|
|
|
2 ω p |
|
|
. 7. 1) |
2 |
|
; |
|
2) |
|
|
|
|
n! |
|
; 3) |
|
|
p2 − 4 |
|
|
; |
||||||||||||||||||||||||||||||||||||||
|
( p2 + 9)( p2 + 1) |
|
|
|
|
|
|
|
|
|
|
|
p3 |
|
|
|
|
pn+1 |
|
( p2 + 4)2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
p( p2 + 4)( p2 + 16) |
|
( p2 + ω2 )2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4) |
|
|
1 |
|
; |
5) |
|
2( p2 + p + 1) |
; |
|
6) |
|
|
2(1 − p2 )(1 + 3p2 ) |
. |
8. |
|
1) |
|
|
|
1 |
|
|
|
|
|
|
; |
|
|
2) |
|
p3 + p2 + p − 1 |
. |
|||||||||||||||||||||||||||||||||||||||||||||
|
( p + 3)2 |
|
|
|
|
|
( p2 − 1)2 |
|
|
|
|
|
|
|
( p2 − 1)4 |
|
|
|
|
|
|
|
p( p2 |
+ 1) |
|
|
|
|
|
|
p( p2 |
+ 1)2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
9. 1) ln |
p |
|
; |
2) ln |
p +1 |
. 10. 1) |
|
|
2 |
|
|
; |
2) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
. 11. 1) |
1− e− p |
|
; 2) |
|
1− 2e− p + e−2p |
; |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
p2(p2 + |
|
|
p2(p2 − 2p + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
p −1 |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
4) |
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|||||||||||||||||||||||
3) |
|
p(1 − e−2 p ) − (1 − e− p )2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.1 ІНДИВІДУАЛЬНІ ТЕСТОВІ ЗАВДАННЯ
1.1. Користуючись властивостями лінійності і подібності, знайдіть зображення функцій.
1.1.1. |
f (t) = sin2 5t. |
|
|||||
1.1.3. |
f (t) = cos |
3 |
|
t |
|
. |
|
|
2 |
|
|||||
|
|
|
|
|
|||
1.1.5. |
f (t) = sin2t cos3t. |
||||||
1.1.7. |
f (t) = cos 2t cos7t . |
||||||
1.1.9. |
f (t) = −sin4 t + sh2 3t. |
||||||
1.1.11. |
f (t) = sht sh3t. |
||||||
1.1.13. |
f (t) = sin4 2t. |
||||||
1.1.15. |
f (t) = sin6t cos4t. |
||||||
1.1.17. |
f (t) = cos 2t cos3t. |
||||||
1.1.19. |
f (t) = sin3 4t. |
||||||
1.1.21. |
f (t) = cos |
3 |
t |
. |
|||
|
|
3 |
|||||
|
|
|
|
|
|
||
354
1.1.2. |
f (t) = cos2 9t. |
|
|
|
|||||
1.1.4. |
f (t) = ch |
t |
ch t. |
||||||
|
|
||||||||
|
3 |
|
|
|
|
|
|
||
1.1.6. |
f (t) = sin4t cos5t. |
||||||||
1.1.8. |
f (t) = ch3 t. |
|
|
|
|
|
|||
1.1.10. |
f (t) = sin 4t sin 3t. |
||||||||
1.1.12. |
f (t) = ch3t − sin2t. |
||||||||
1.1.14. |
f (t) = cos |
4 |
|
t |
. |
|
|
||
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
||
1.1.16. |
f (t) = sin4t sin 8t. |
||||||||
1.1.18. |
f (t) = cos 2t cos2t . |
||||||||
1.1.20. |
f (t) = cos3 3t. |
||||||||
1.1.22. f (t) = sh |
2t |
|
ch |
3t |
. |
||||
|
|
|
|||||||
|
|
|
|
5 |
|
|
5 |
|
|
http://vk.com/studentu_tk, http://studentu.tk/

1.1.23. |
f (t) = sht ch 2t. |
1.1.24. |
f (t) = ch3t sh t. |
1.1.25. |
f (t) = sh2 3t. |
1.1.26. |
f (t) = ch 3t ch 2t. |
1.1.27. |
f (t) = sh3t. |
1.1.28. |
f (t) = ch3 4t. |
1.1.29. |
f (t) = sin3t cos5t. |
1.1.30. |
f (t) = sin 2t sin2 t. |
1.2. Користуючись властивостями 40
1.2.1. |
f (t − 2) = (t − 2)2 η(t − 2). |
1.2.3. |
f (t − 4) = cos2 (t − 4)η(t − 4). |
1.2.5. |
f (t − 5) = et −5 η(t − 5). |
1.2.7. |
f (t − 2) = sin2 (t − 2)η(t − 2). |
1.2.9. |
f (t) = e− αt cos2βt. |
1.2.11. |
f (t) = et cos2t. |
1.2.13. |
f (t) = e2t sh3t. |
1.2.15. |
f (t) = e3t sin2 2t. |
1.2.17. |
f (t) = e−2t t3. |
1.2.19. |
f (t) = e3tsh 4t. |
і50, знайдіть зображення функцій.
1.2.2.f (t − 3) = sin2 t − 3 η(t − 3).
|
|
|
|
|
2 |
|
1.2.4. |
f (t − 1) = e1−t η(t − 1). |
|||||
1.2.6. |
f (t − 3) = cos3 (t − 3)η(t − 3). |
|||||
1.2.8. |
f (t) = e−3t |
(2t − 1). |
||||
1.2.10. |
f (t) = e− αt sin2βt. |
|||||
1.2.12. |
f (t) = e−tt4 . |
|
|
|
||
1.2.14. |
f (t) = e4t cos t. |
|
|
|||
1.2.16. |
f (t) = e2t sin5t. |
|
|
|||
1.2.18. |
f (t) = e−3t t2 . |
|
|
|
||
1.2.20. |
f (t) = e |
−t |
cos |
2 |
t |
. |
|
|
2 |
||||
|
|
|
|
|
|
|
1.2.21. |
f (t) = e−3tsin2t. |
|
1.2.22. |
f (t) = e−2tsin 4t. |
|
|||
1.2.23. |
f (t − 3) = e2(t−3) η(t − 3). |
1.2.24. |
f (t − 1) = cos3 |
t − 1 |
|
η(t − 1). |
||
|
||||||||
|
|
|
|
|
2 |
|
|
|
1.2.25. |
f (t − 4) = sin2 |
t − 4 |
η(t − 4). |
1.2.26. |
f (t) = e−4t+ 2η(t − 3). |
|||
|
||||||||
|
4 |
|
|
|
|
|
|
|
1.2.27. |
f (t) = e−3t cos4t. |
|
1.2.28. |
f (t) = e−tt6 . |
|
|||
1.2.29. |
f (t) = e−t ch5t. |
|
1.2.30. |
f (t) = (3t − 2)e2t . |
|
|||
1.3. Користуючисьвластивостями60 або70, знайдітьзображенняфункцій.
1.3.1. |
f (t) = t sin2 2t. |
1.3.2. |
f (t) = t sin3 t. |
1.3.3. |
f (t) = tcos2t. |
1.3.4. |
f (t) = t sin3t. |
1.3.5. |
f (t) = t cos ωt. |
1.3.6. |
f (t) = t sh t. |
355
http://vk.com/studentu_tk, http://studentu.tk/

1.3.7. |
f (t) = t ch t. |
1.3.9. |
f (t) = t2 cos ωt. |
1.3.11. |
f (t) = t sin ωt shωt. |
1.3.13. |
f (t) = t2sin 3t. |
1.3.15. |
f (t) = t2 sh t. |
1.3.17. |
f (t) = t cos 5t. |
1.3.19. |
f (t) = t e−5t . |
1.3.21. |
f (t) = t(et − ch 2t). |
1.3.23. |
f (t) = t sh 3t. |
1.3.25. |
f (t) = t sin t sh t. |
1.3.27. |
f (t) = t cos t ch t. |
1.3.29. |
f (t) = t2e−2t . |
1.3.8. |
f (t) = t ch ωt. |
1.3.10. |
f (t) = t2sh t. |
1.3.12. |
f (t) = t cosωt chωt. |
1.3.14. |
f (t) = t2ch5t. |
1.3.16. |
f (t) = t2 ch 2t. |
1.3.18. |
f (t) = t sin 3t. |
1.3.20. |
f (t) = t2cos t. |
1.3.22. |
f (t) = (t + 1)sin 2t. |
1.3.24. |
f (t) = (t2 − 1) sh 2t. |
1.3.26. |
f (t) = t2ch 2t. |
1.3.28. |
f (t) = t ch 2t. |
1.3.30. |
f (t) = t2e4t . |
1.4. Користуючисьвластивостями80 або90, знайдітьзображенняфункцій.
1.4.1. |
f (t) = ∫t |
τsin3τd τ. |
|
0 |
|
1.4.3. |
t |
|
f (t) = ∫ |
τsh 2τd τ. |
|
|
0 |
|
|
t |
|
1.4.5. |
f (t) = ∫ |
τch ωτd τ. |
|
0 |
|
1.4.7. |
t |
|
f (t) = ∫ sin (2τ − 3)d τ. |
||
|
0 |
|
|
t |
|
1.4.9. |
f (t) = ∫ e−3τ sin 5τ d τ. |
|
|
0 |
|
1.4.2. |
f (t) = ∫t |
(2τ − 3)cosτd τ. |
|||||
|
0 |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
1.4.4. |
f (t) = ∫ cos2 ωτd τ. |
||||||
|
0 |
|
|
|
|
|
|
|
t |
τ2 e− τ d τ. |
|||||
1.4.6. |
f (t) = ∫ |
||||||
|
0 |
|
|
|
|
|
|
|
t |
|
τ |
3 |
e |
2τ |
|
1.4.8. |
f (t) = ∫ |
|
|
|
d τ. |
||
|
|
|
6 |
|
|||
|
0 |
|
|
|
|
|
|
t
1.4.10. f (t) = ∫ e−4τ cos8τ d τ.
0
t
1.4.11. f (t) = ∫ τ cos 4τd τ.
0
1.4.13. f (t) = 1− cos2t . t
356
t
1.4.12. f (t) = ∫ (τ − 2)cos2τd τ.
0
t
1.4.14. f (t) = ∫ (τ − 1)sh 4τd τ.
0
http://vk.com/studentu_tk, http://studentu.tk/
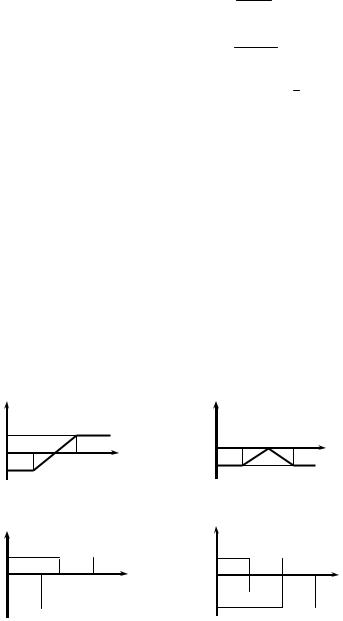
1.4.15. |
f (t) = |
|
et − 1 |
. |
|
|
|
|
|
|
|||
|
|
t |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4.17. |
f (t) = |
|
sin2t |
. |
|
|
|
|
|
|
|||
|
|
t |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4.19. |
f (t) = |
et − 1− t |
. |
|
|
||||||||
|
|
t |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
1.4.21. |
f (t) = |
e−at sin t |
|
. |
|
|
|||||||
|
|
|
t |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
1.4.23. |
f (t) = |
cos 3t − cos 2t |
. |
||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
1.4.25. |
f (t) = |
1 |
− eat |
. |
|
|
|
|
|||||
|
|
t et |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
1.4.27. |
f (t) = |
cos |
23t |
|
. |
|
|
|
|
||||
|
|
t |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4.29. |
f (t) = |
cos t − cos 2t |
. |
||||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
1.4.16. f (t)
1.4.18. f (t)
1.4.20. f (t)
1.4.22. f (t)
1.4.24. f (t)
1.4.26. f (t)
1.4.28. f (t)
1.4.30. f (t)
=1 − e−t . t
=1− cos t . t
=(1 − e2t )et 1 .
t
= |
sin 7t sin 3t |
. |
|||||||
|
|
|
|||||||
|
|
t |
|
|
|
|
|
|
|
= |
1− cos t |
e |
−t |
. |
|
||||
|
t |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
= |
|
e− at sin2bt |
. |
|
|
||||
|
t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
= e−2t sin 2t |
1 |
. |
|||||||
|
|||||||||
|
|
|
|
|
|
|
t |
|
|
= |
|
et − e−t |
|
. |
|
|
|
|
|
|
t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
1.5. Знайдіть зображення функцій, заданих графічно.
1.5.1. |
|
|
|
1.5.2. |
|
|
|
f(t) |
|
|
|
f(t) |
|
|
|
1 |
|
|
|
O |
a |
2a |
3a |
O |
a |
2a 3a |
t |
|
|
t |
|
–1 |
|
|
|||||
–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.5.3. |
|
|
|
|
|
|
1.5.4. |
|
|
|
|
|
f(t) |
|
|
|
|
|
|
f(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
O |
|
|
|
|
|
t |
О |
a |
|
|
|
|
2 3 |
5 |
2a |
3a |
|
t |
|||||||
|
–1 |
|
||||||||||
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
357
http://vk.com/studentu_tk, http://studentu.tk/

1.5.5. |
|
|
|
1.5.6. |
|
|
|
|
f(t) |
|
|
|
f(t) |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
O |
a |
2a |
3a t |
O |
a |
2a |
3a t |
|
–1 |
–1 |
|||||||
|
|
|
|
|
|
1.5.7. |
|
|
|
|
|
1.5.8. |
|
|
|
|
|
|
|
|
|
|
|
|
f(t) |
|
|
|
|
|
|
f(t) |
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
O |
a |
2a |
3a t |
O |
a |
2a |
3a t |
|||||
|
|
|||||||||||
1.5.9.
f(t)
1
O
a 2a t
–1
1.5.11.
f(t) |
|
|
|
1 |
|
3a |
|
O |
a |
||
5a t |
|||
–1 |
|||
|
|
1.5.13.
f(t) |
|
|
|
1 |
|
|
|
O |
a 2a 3a |
t |
|
–1 |
|||
|
|
358
1.5.10.
f(t) |
|
|
|
|
1 |
|
|
|
|
O |
a |
2a |
t |
|
–1 |
||||
|
|
|
1.5.12.
f(t) |
|
|
1 |
|
|
O |
a 2a 3a 4a |
t |
|
1.5.14.
f(t) |
|
|
|
|
1 |
|
|
|
|
O |
a |
2a |
t |
|
–1 |
||||
|
|
|
http://vk.com/studentu_tk, http://studentu.tk/

1.5.15. |
|
|
1.5.16. |
|
|
|
|
|
|
f(t) |
|
|
f(t) |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
1 |
|
|
1 |
|
|
|
|
|
|
O |
a 2a 3a |
t |
O |
|
|
|
|
|
|
a 2a |
3a |
t |
|||||||
–1 |
–1 |
||||||||
|
|
|
|
|
|
|
|||
1.5.17. |
|
|
|
1.5.18. |
|
|
|
|
f(t) |
|
|
|
f(t) |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
O |
|
|
t |
O |
|
|
t |
|
a |
2a |
a |
2a |
|||||
|
–1 |
|||||||
|
|
|
|
|
|
|
||
–2 |
|
|
|
–2 |
|
|
|
1.5.19. |
|
|
1.5.20. |
|
|
|
|
f(t) |
|
|
f(t) |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
O |
3a |
t |
O |
a 2a |
3a |
t |
|
a 2a |
|
||||||
–1 |
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
||
1.5.21. |
|
|
1.5.22. |
|
|
|
|
f(t) |
|
|
f(t) |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
O |
a |
2a 3a t |
O |
a |
2a |
t |
|
–1 |
–1 |
||||||
|
|
|
|
|
1.5.23. |
|
|
1.5.24. |
|
|
|
f(t) |
|
|
f(t) |
|
|
|
|
|
|
|
|
||
1 |
|
|
1 |
|
|
|
|
|
O |
|
|
||
O |
a 2a 3a |
t |
a 2a |
3a t |
||
–1 |
||||||
|
|
|
359
http://vk.com/studentu_tk, http://studentu.tk/
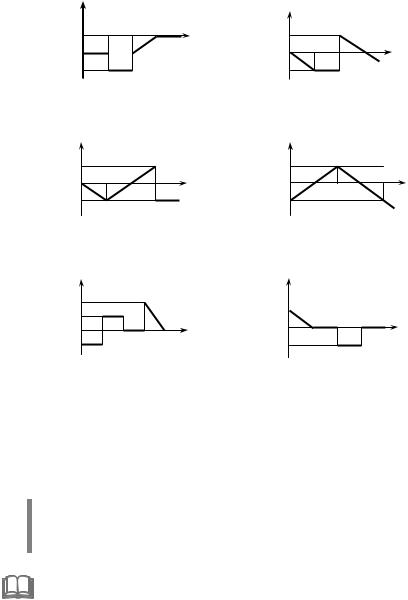
1.5.25. |
|
|
1.5.26. |
|
|
|
f(t) |
|
|
f(t) |
|
|
|
|
|
|
|
|
||
O |
a 2a |
3a t |
1 |
a 2a |
3a |
|
–1 |
O |
|||||
|
|
|
t |
|||
–2 |
|
|
–1 |
|
||
|
|
|
|
1.5.27. |
|
|
1.5.28. |
|
|
|
|
f(t) |
|
|
f(t) |
|
|
|
|
1 |
a 2a |
3a |
1 |
|
|
|
|
O |
O |
a |
2a 3a |
4at |
|||
|
t |
||||||
–1 |
|
–1 |
|||||
|
|
|
|
|
1.5.29. |
|
|
|
1.5.30. |
|
|
|
f(t) |
|
|
|
f(t) |
|
|
|
2 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
||
|
|
|
O |
|
|
||
O |
|
|
t |
a |
2a 3a t |
||
a 2a 3a 4a |
|||||||
–1 |
–1 |
||||||
|
|
|
|
|
|||
Тема 2. ВІДШУКАННЯ ОРИГІНАЛУ ЗА ЙОГО ЗОБРАЖЕННЯМ.
ЗАСТОСУВАННЯ ПЕРЕТВОРЕННЯ ЛАПЛАСА ДО РОЗВ’ЯЗАННЯ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ. ФОРМУЛА ДЮАМЕЛЯ
Обернене перетворення Лапласа. Елементарні засоби відшукання оригіналів. Перша та друга теореми розкладання. Розв’я- зання лінійних диференціальних рівнянь. Інтеграл Дюамеля. Розв’язання систем лінійних диференціальних рівнянь
Література: [4, розділ 2, пп. 2.4—2.7], [5, гл.2, пп. 2.11— 2.12], [12, розділ 32, §3—4], [13, розділ 2, §12—14], [15, розділ 16, п.п. 16.2.6—16.2.8], [17, розділ 9, §33—34]
360
http://vk.com/studentu_tk, http://studentu.tk/
