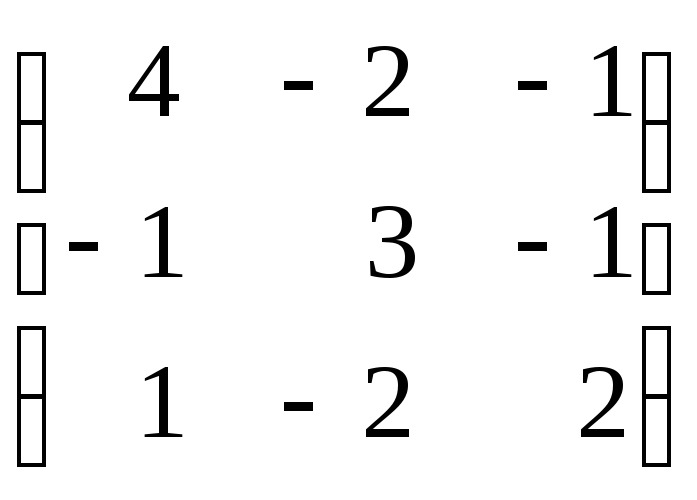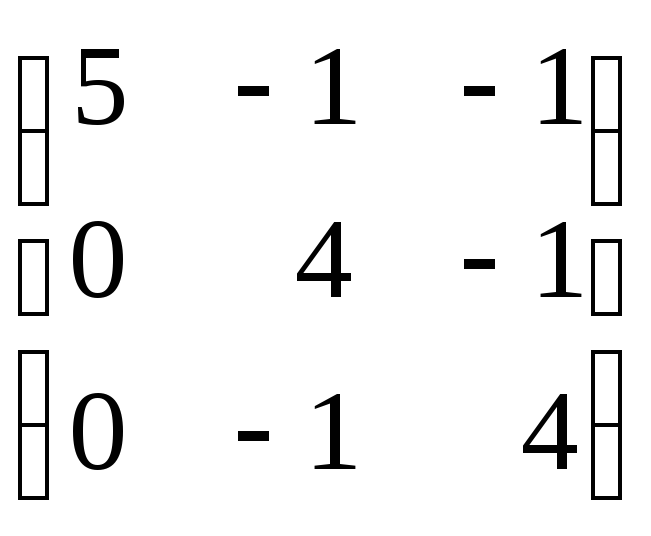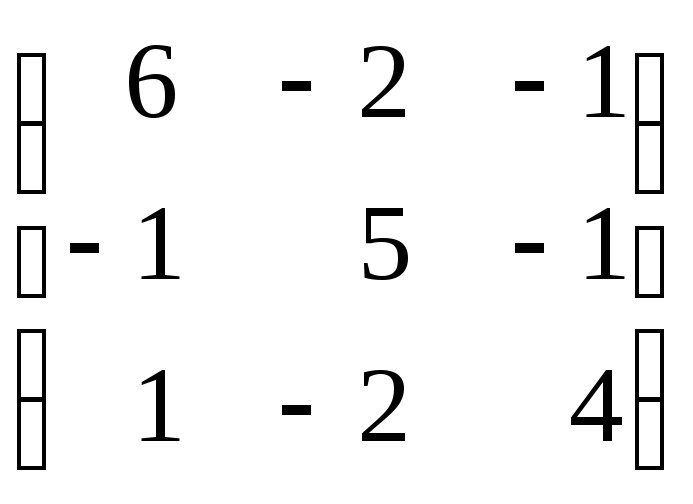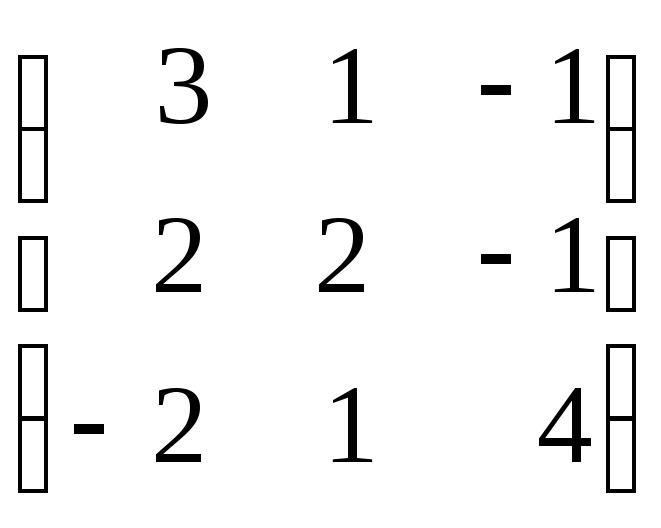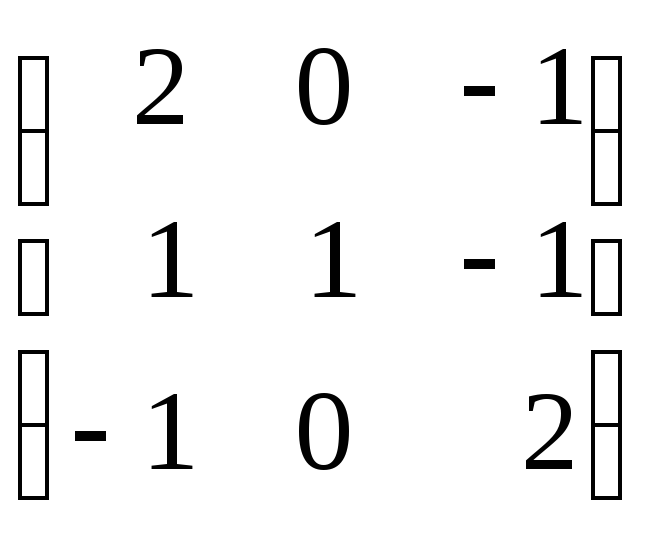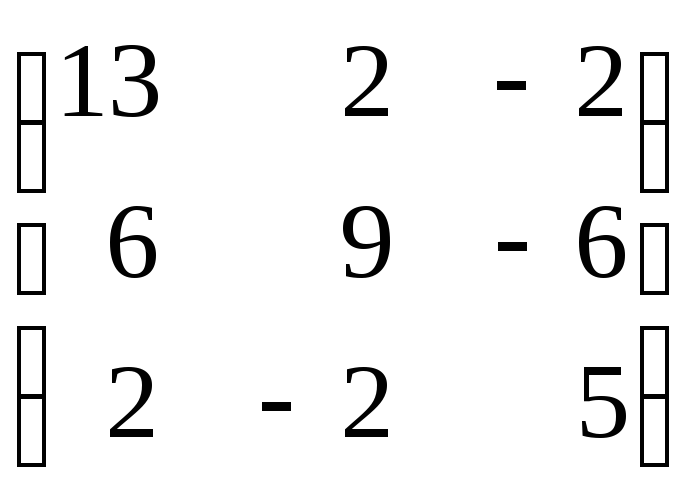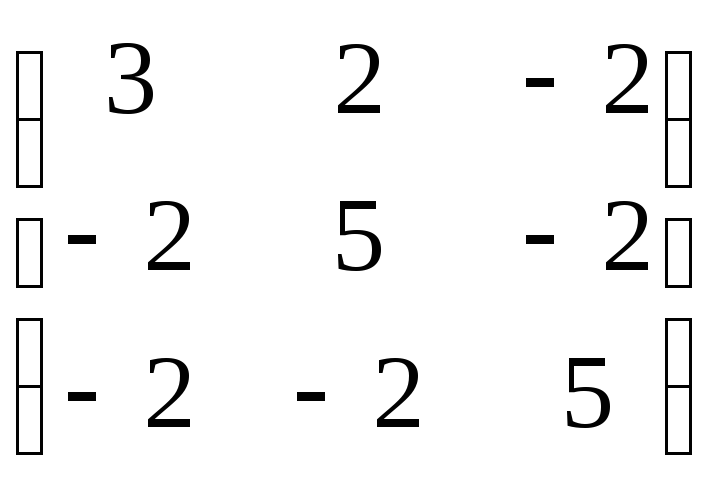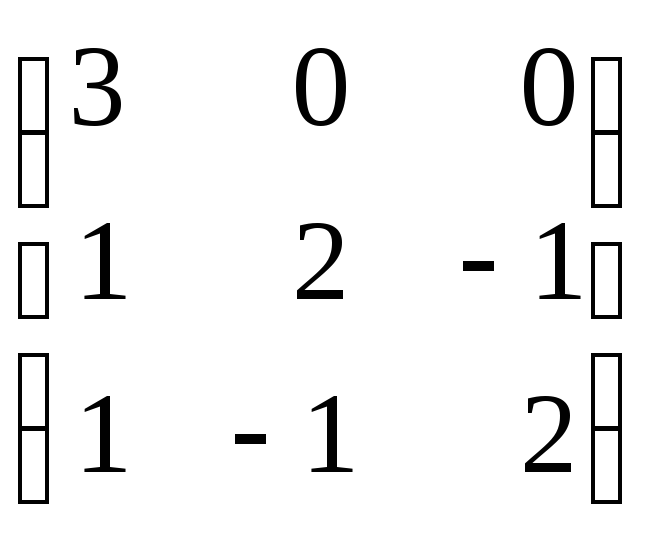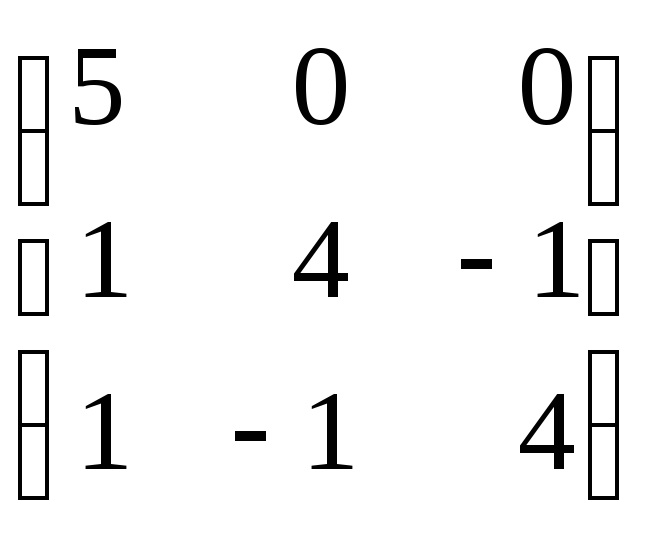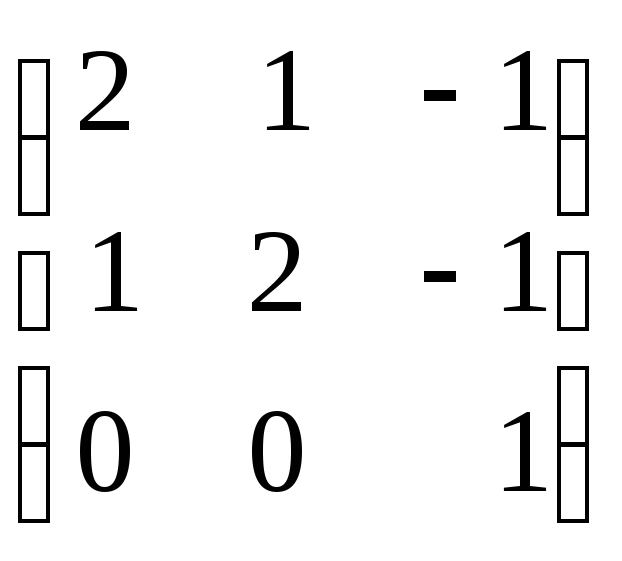Типовой расчет №2 ВЕКТОРНАЯ АЛГЕБРА
.docТИПОВОЙ РАСЧЕТ №2
ВЕКТОРНАЯ АЛГЕБРА
Повторите теоретический материал.
-
Векторы. Линейные операции над векторами.
-
Проекция вектора на ось. Координаты вектора.
-
Скалярное произведение векторов и его свойства. Приложения скалярного произведения.
-
N-мерный вектор. Векторное пространство.
-
Линейно зависимые и линейно независимые системы векторов. Базис векторного пространства.
-
Евклидово пространство.
Задание 6.
В некотором базисе даны 4 вектора:
![]() Показать, что векторы
Показать, что векторы
![]() образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора
![]() в этом базисе.
в этом базисе.
Задание 7. Решить задачу.
-
Найти модуль вектора
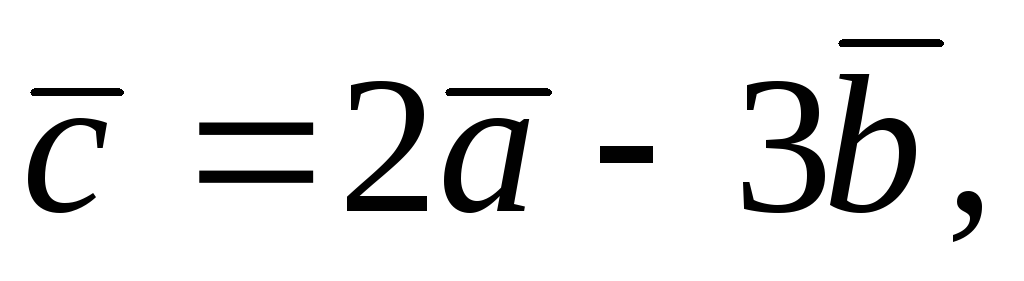 если
если
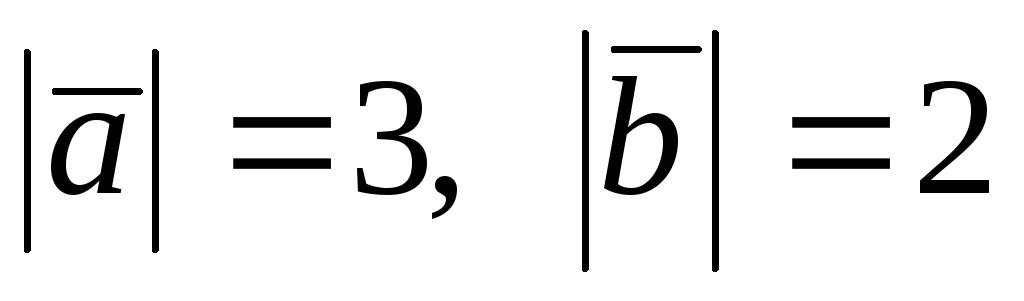 ,
угол между векторами
,
угол между векторами
 и
и
 равен 120
о .
равен 120
о . -
Даны:
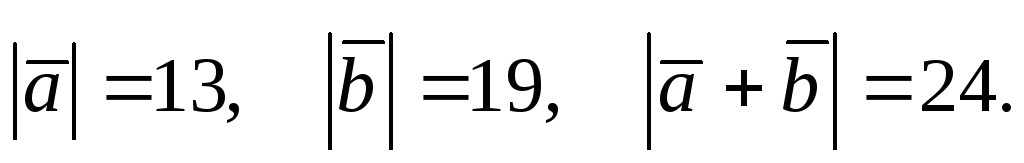 Вычислить
Вычислить
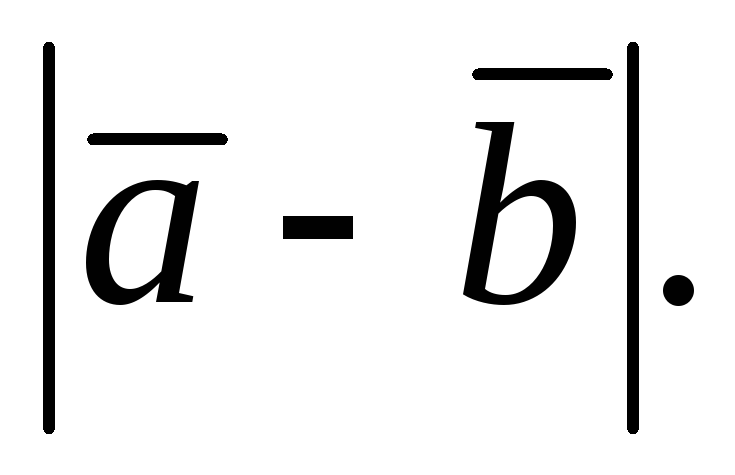
-
Даны точки А(1,2,1), В(2,-1,3) и С(3,
 ).
При каких значениях
).
При каких значениях
 и
и
 точка С
лежит на прямой АВ
?
точка С
лежит на прямой АВ
? -
Найти проекцию вектора
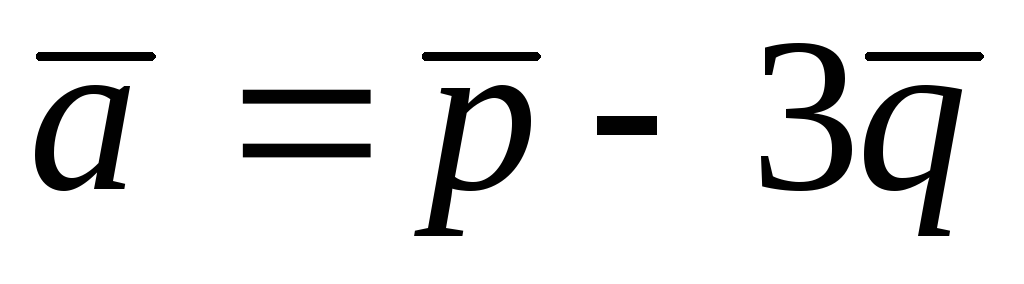 на вектор
на вектор
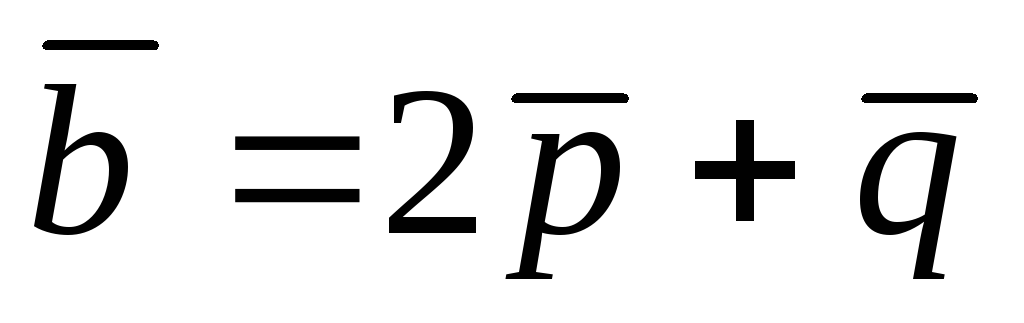 ,
если
,
если
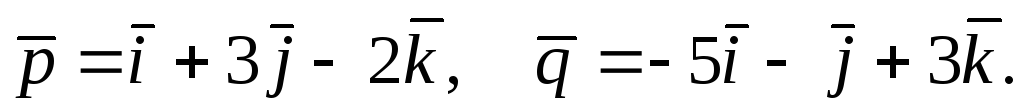
-
Векторы
 и
и
 образуют угол
образуют угол
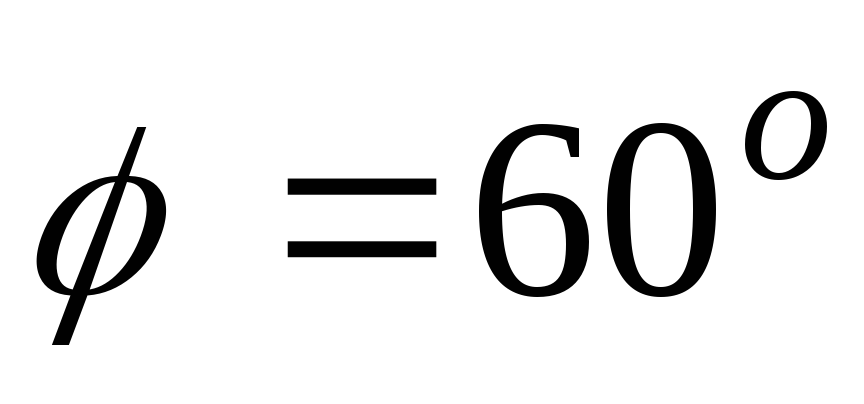 ,
причем
,
причем
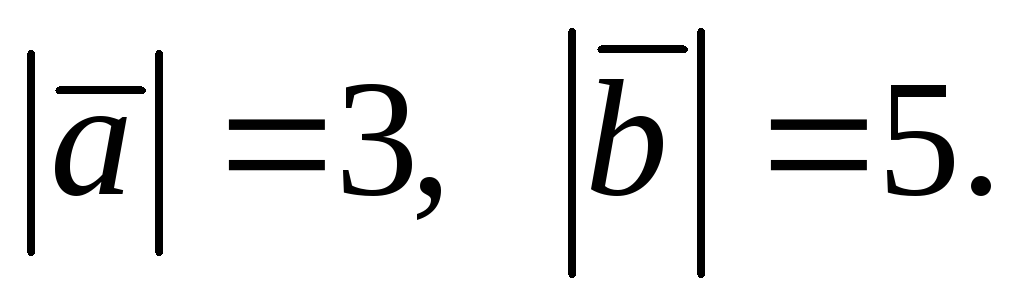 Определить
Определить
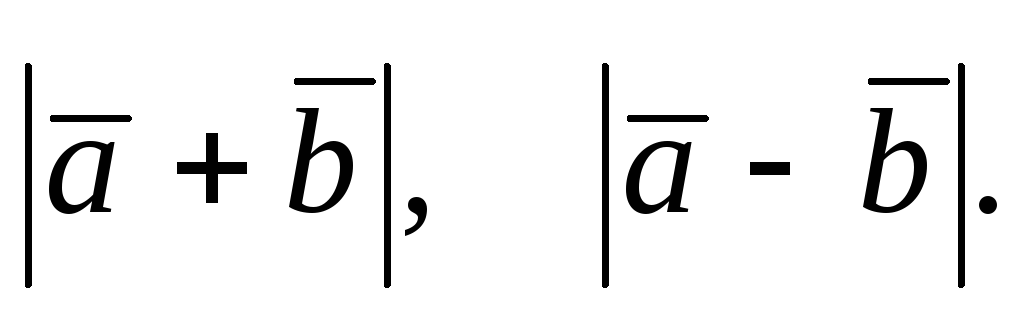
-
Даны векторы:
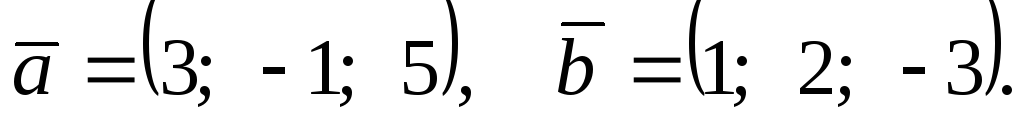 .
Найти вектор
.
Найти вектор
 при условии, что он перпендикулярен к
оси OZ
и удовлетворяет условиям:
при условии, что он перпендикулярен к
оси OZ
и удовлетворяет условиям:
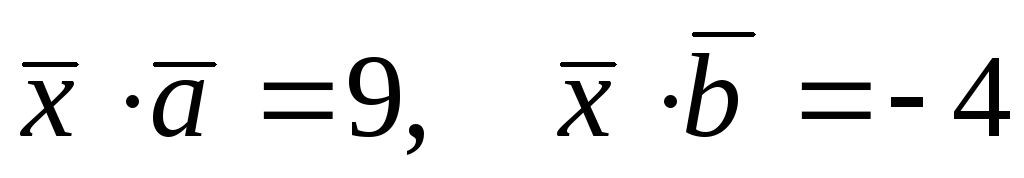 .
. -
Векторы
 и
и
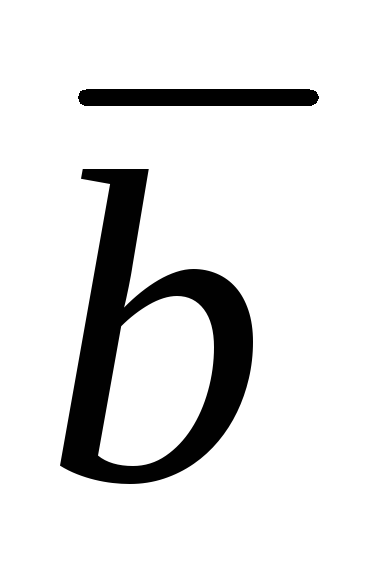 образуют угол
образуют угол
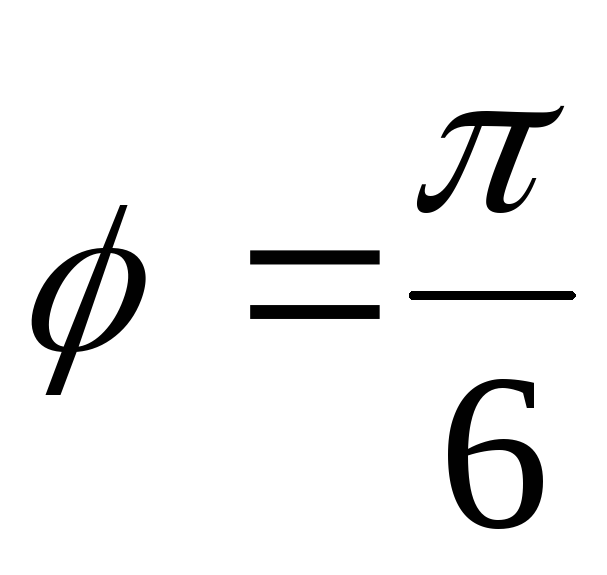 .
Зная, что
.
Зная, что
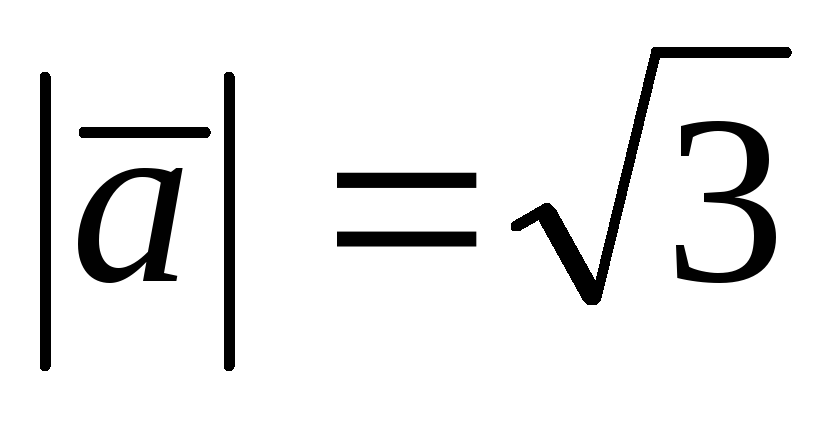 ,
,
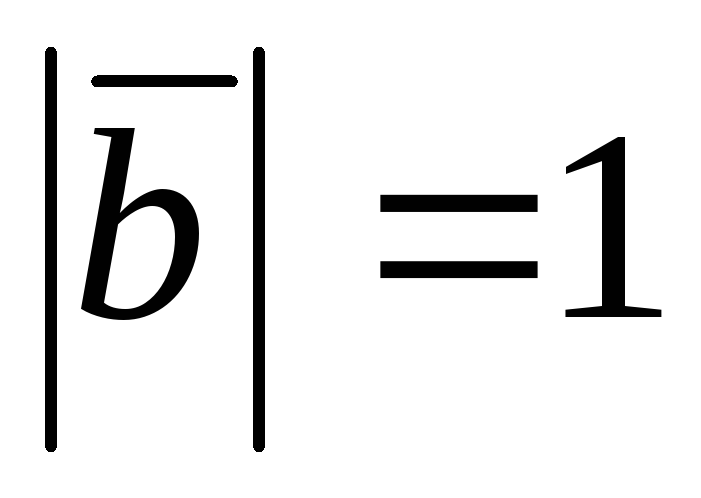 ,
вычислить угол
,
вычислить угол
 между векторами
между векторами
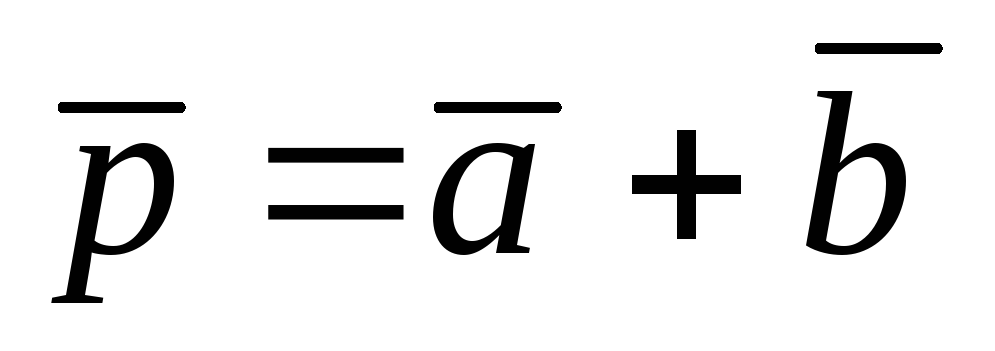 и
и
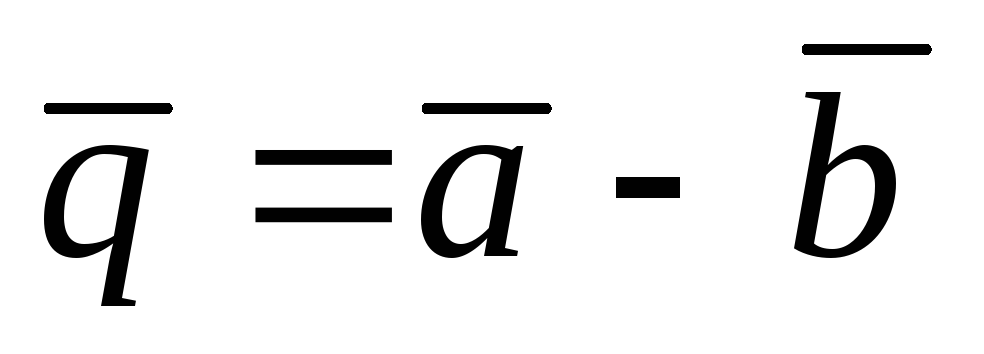 .
. -
Доказать, что четырехугольник с вершинами А (2;1;-4), В(1;3;5), С(7;2;3), D(8;0;-6) является параллелограммом. Найти длины его сторон.
-
Найти модуль вектора
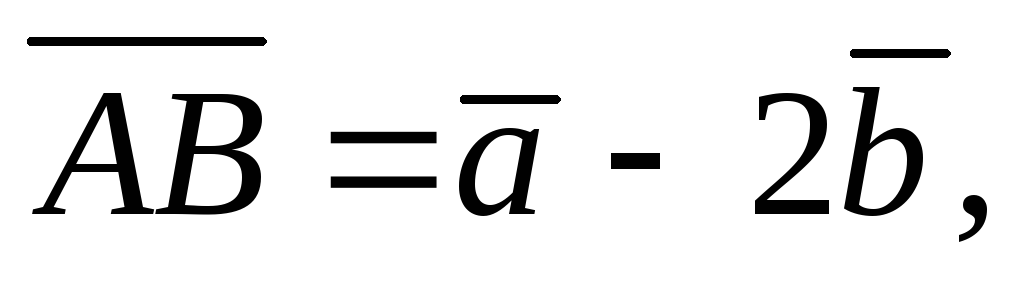 если
если
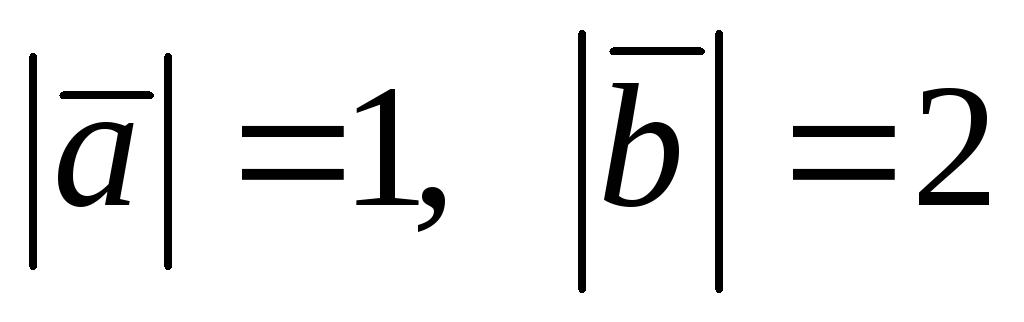 ,
а угол между ними равен
,
а угол между ними равен
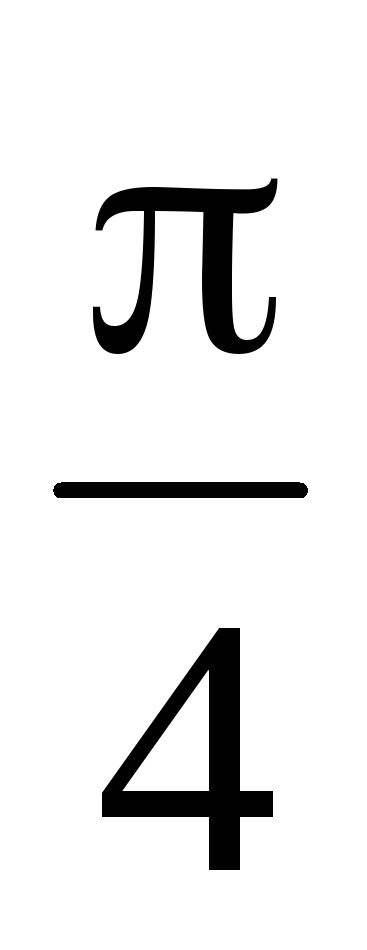 .
. -
Даны:
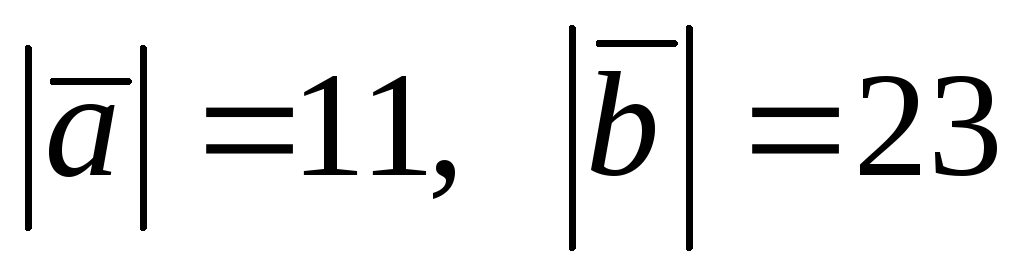 и
и
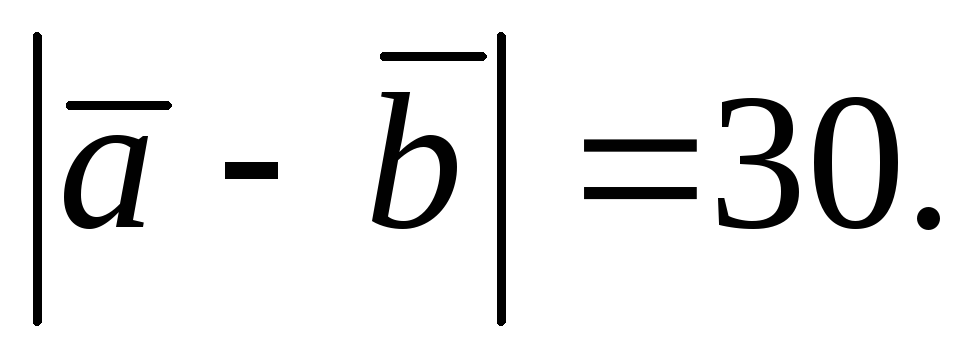 Определить
Определить
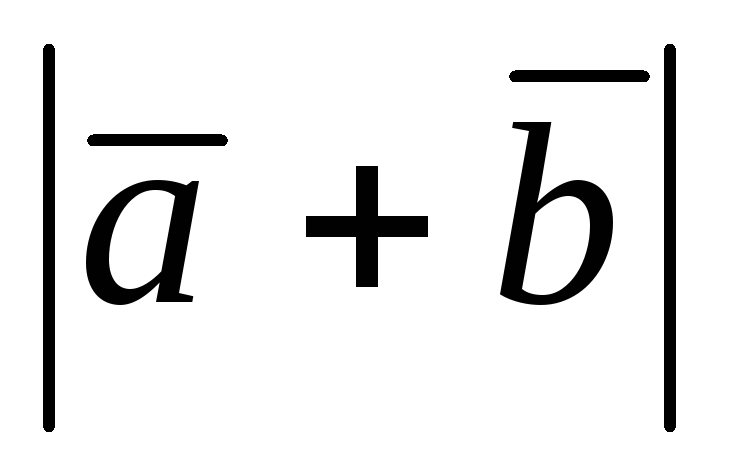 .
. -
Определить координаты и модули диагоналей параллелограмма, построенного на векторах
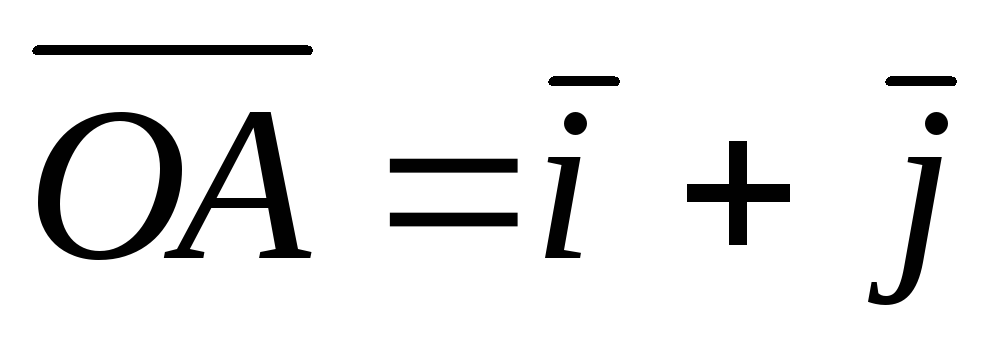 и
и

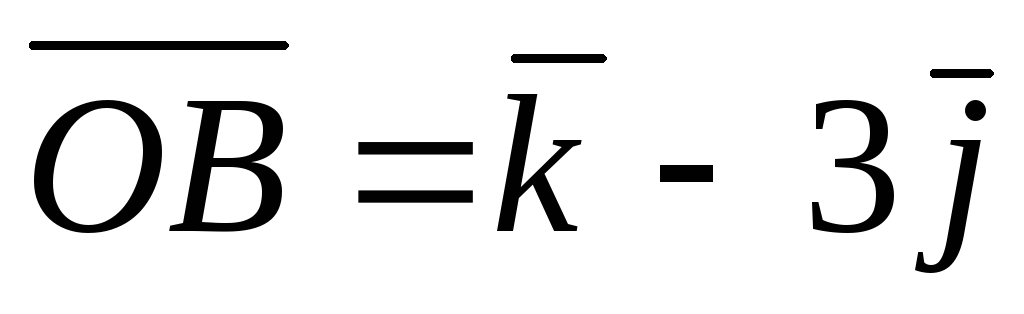 .
. -
Доказать, что точки А( -2; 1; 4), В( 0; -1; -3), С( 6; -3; -10) лежат на одной прямой, причем точка В расположена между точками А и С.
-
Векторы
 и
и
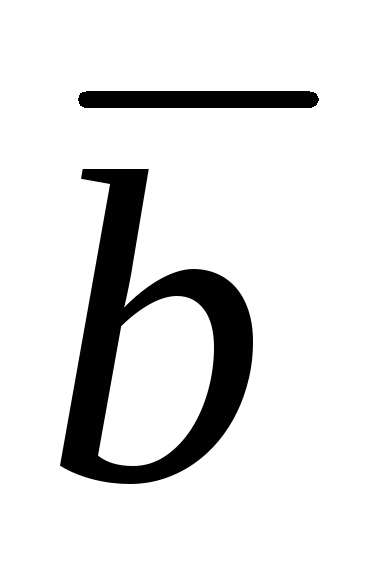 взаимно перпендикулярны, а вектор
взаимно перпендикулярны, а вектор
 образует с ними углы, равные
образует с ними углы, равные
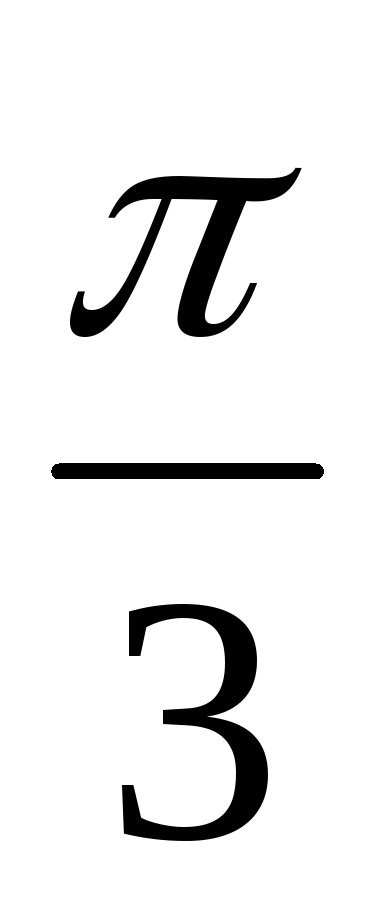 .
Зная, что
.
Зная, что
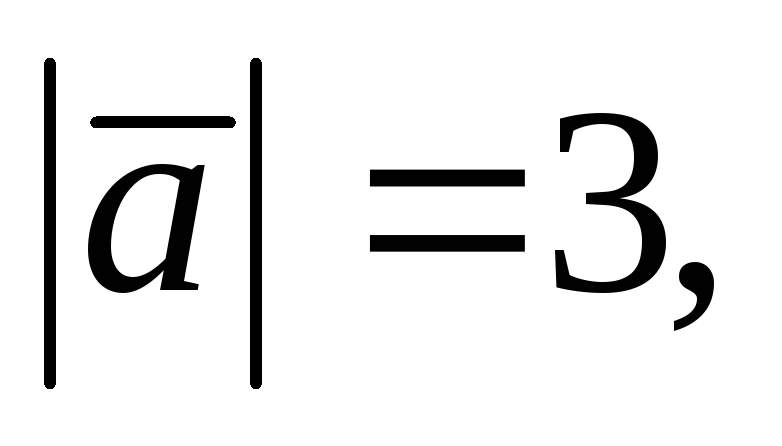
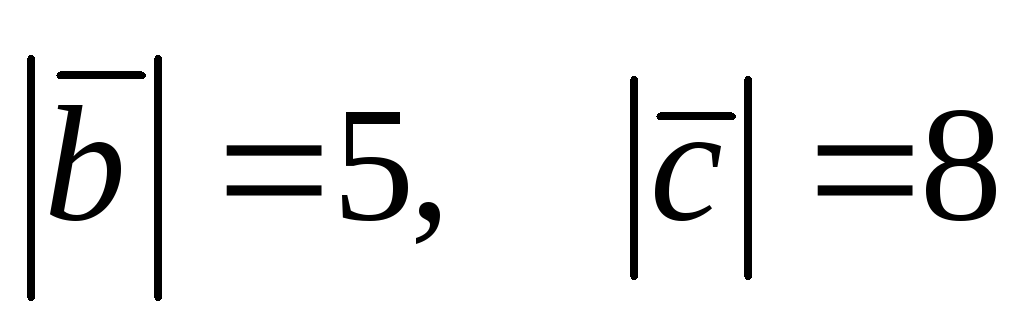 ,
вычислить
,
вычислить
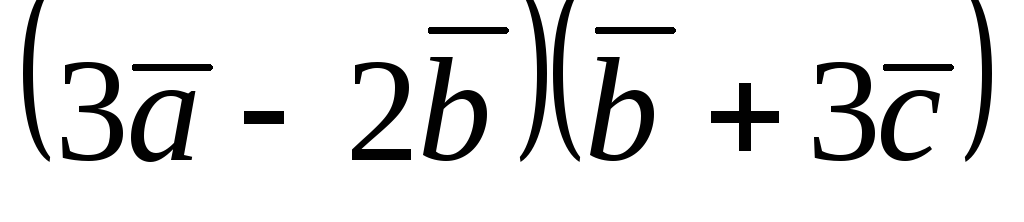 .
. -
Даны три вектора:
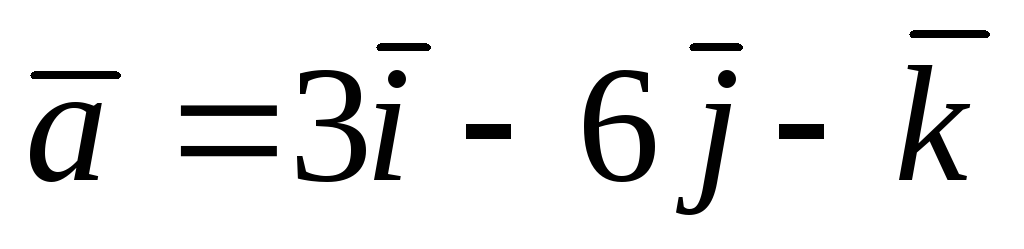 ,
,
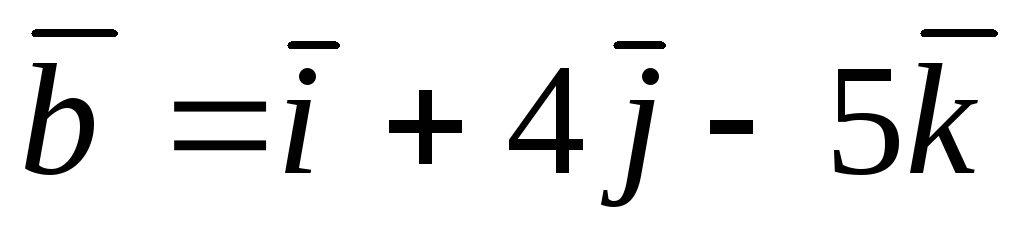 и
и
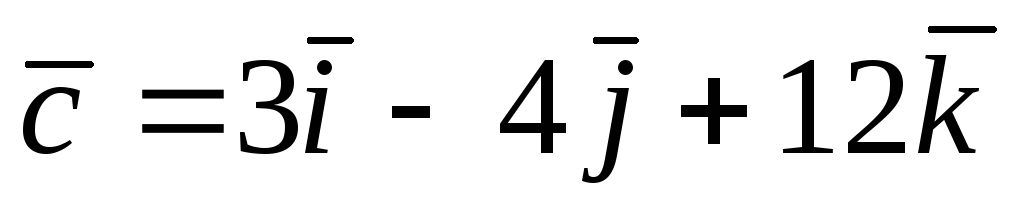 .
Вычислить проекцию вектора
.
Вычислить проекцию вектора
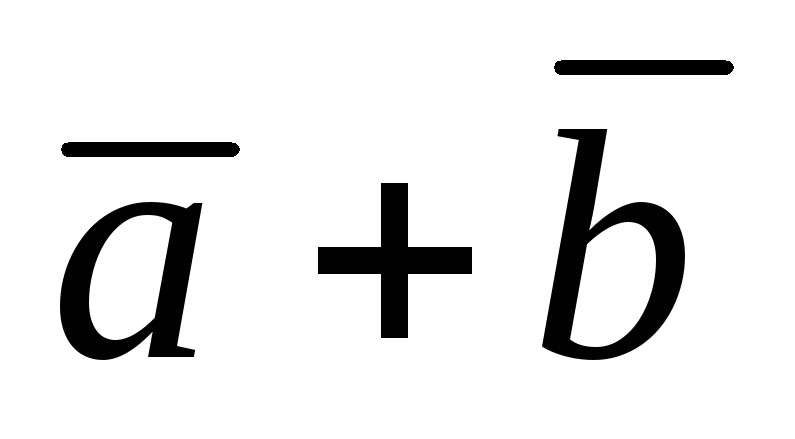 на направление вектора
на направление вектора
 .
. -
Вычислить внутренние углы треугольника АВС, если А( 1; 2; 1), В( 3; -1;7), С( 7; 4; -2). Убедиться, что этот треугольник равнобедренный.
-
Даны точки А( 7; -4; 1), В( 12; -3; 1), С( 10; 1; 5). Требуется: 1) записать векторы
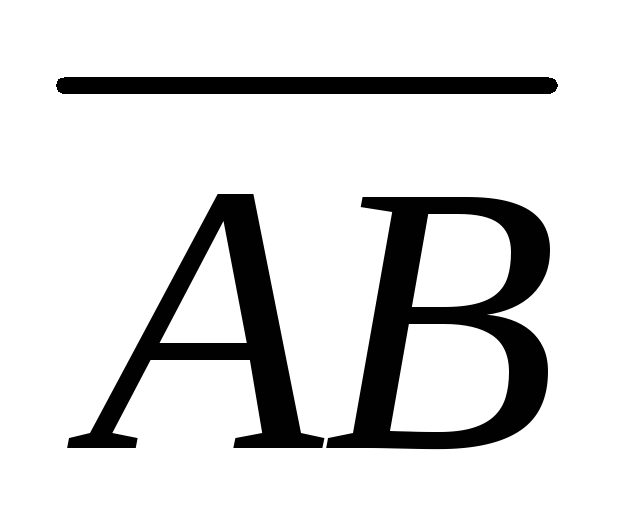 и
и
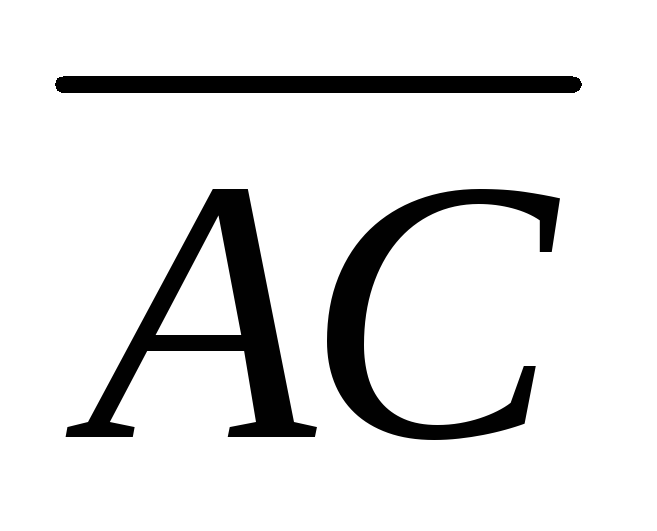 в системе орт и найти модули этих
векторов; 2) найти угол между векторами
в системе орт и найти модули этих
векторов; 2) найти угол между векторами
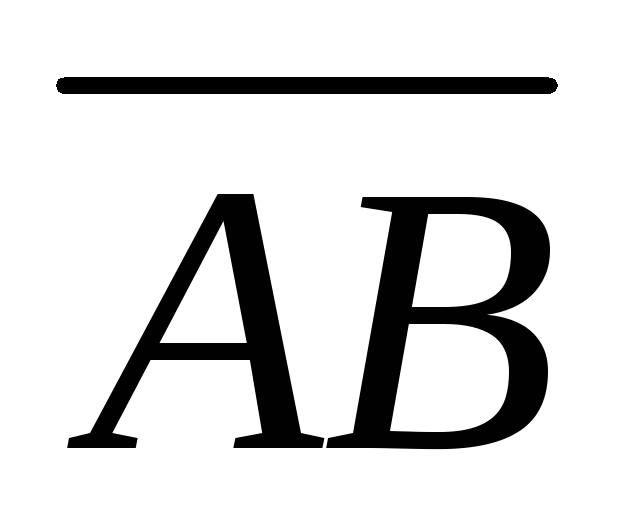 и
и
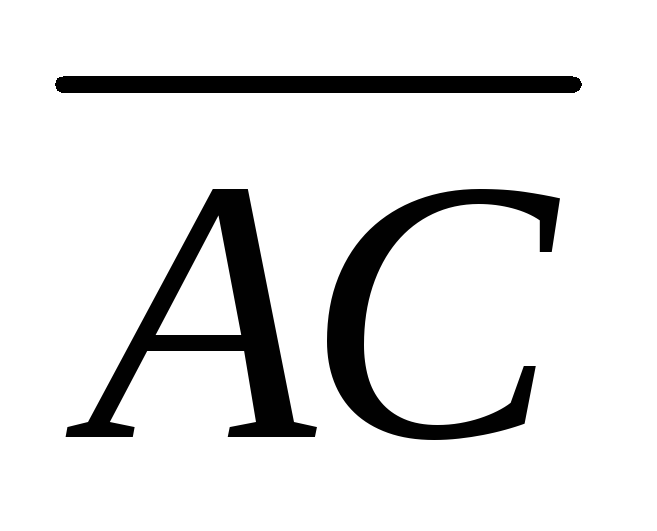 .
. -
Определить при каком значении
 векторы
векторы
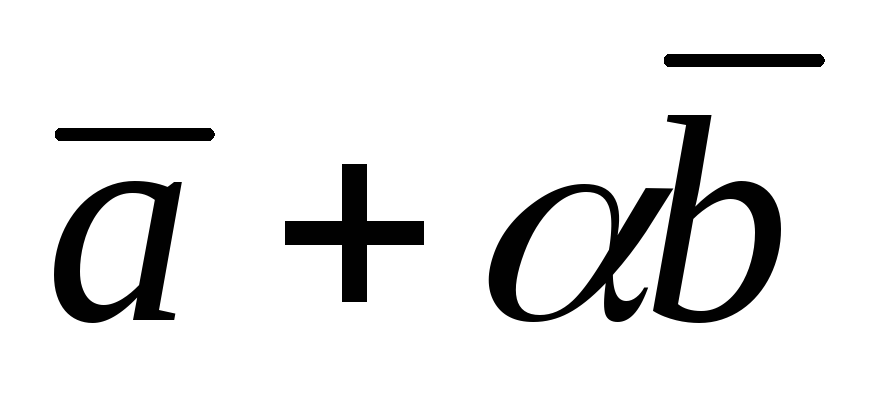 и
и
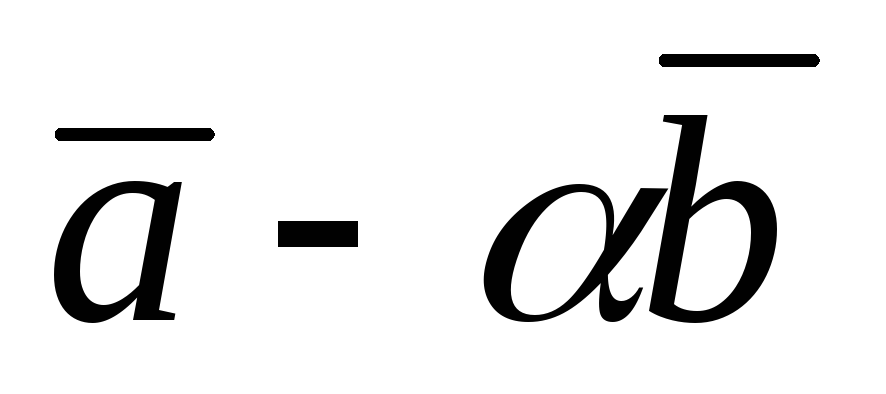 взаимно перпендикулярны, если
взаимно перпендикулярны, если
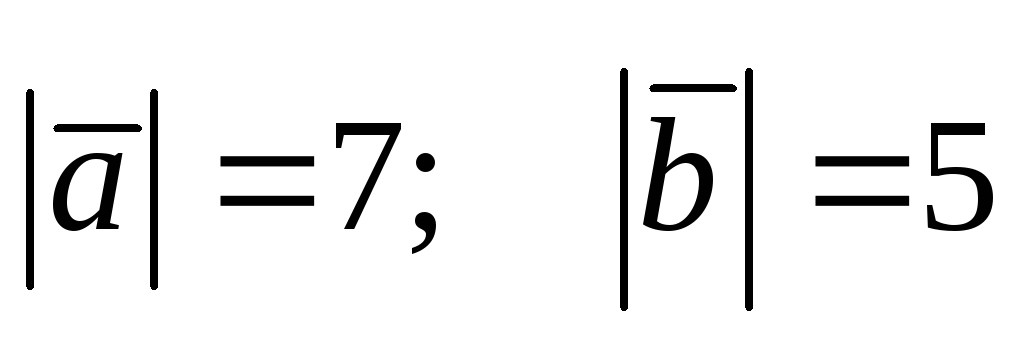 .
. -
Найти вектор
 ,
зная, что он перпендикулярен векторам
,
зная, что он перпендикулярен векторам
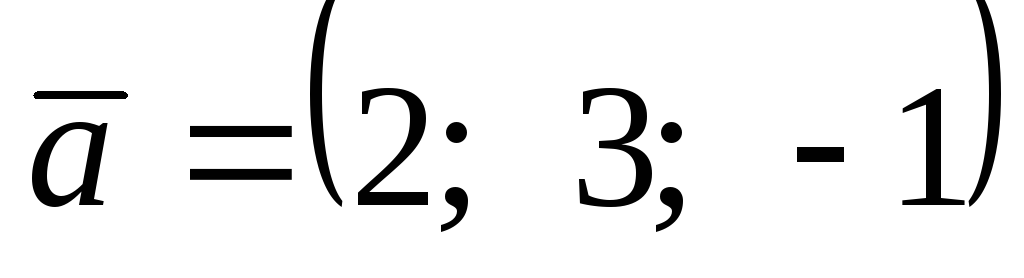 и
и
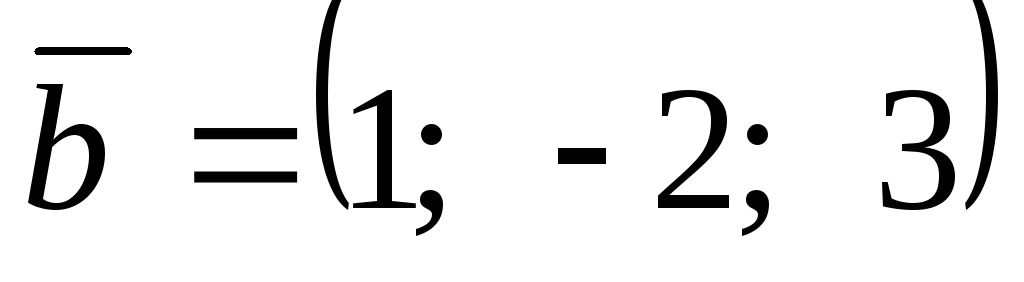 и удовлетворяет условию
и удовлетворяет условию
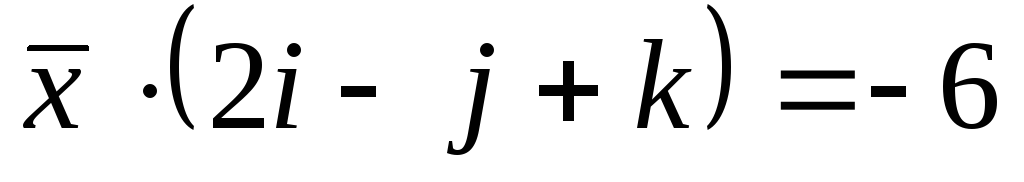 .
. -
Векторы
 и
и
 образуют угол
образуют угол
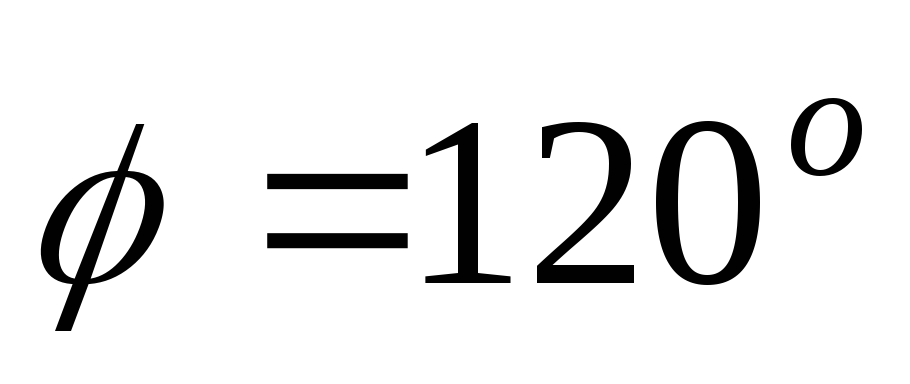 ,
причем
,
причем
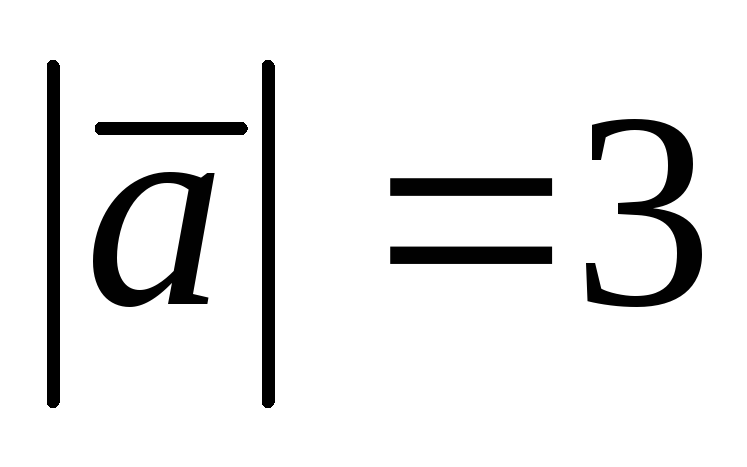 ,
,
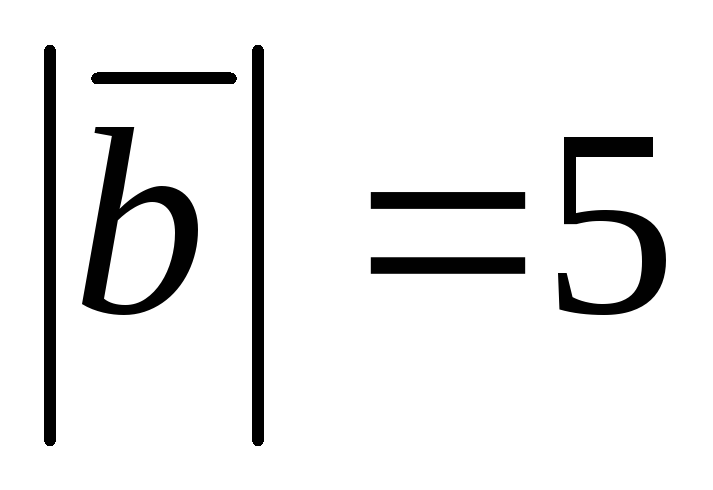 .
Определить
.
Определить
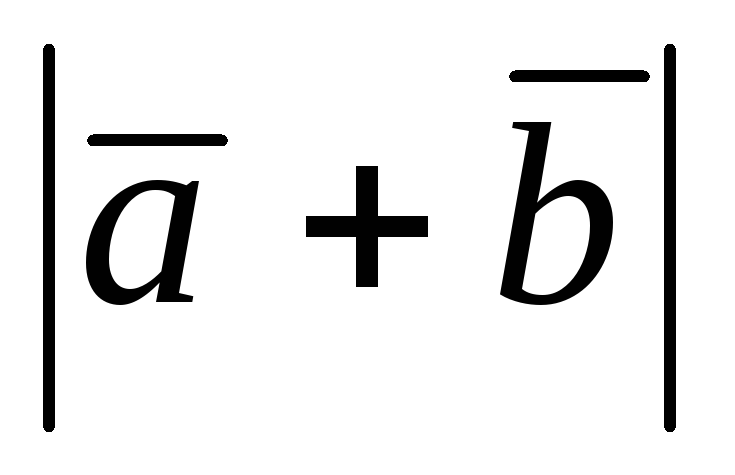 и
и
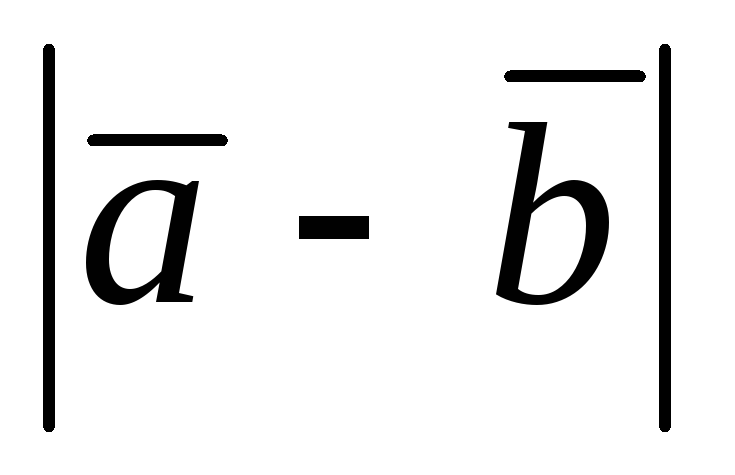 .
. -
Даны точки А( -2; 3; -4), В( 3; 2; 5), С( -1; -1; 2), D( 3; 2; -4). Вычислить проекцию вектора
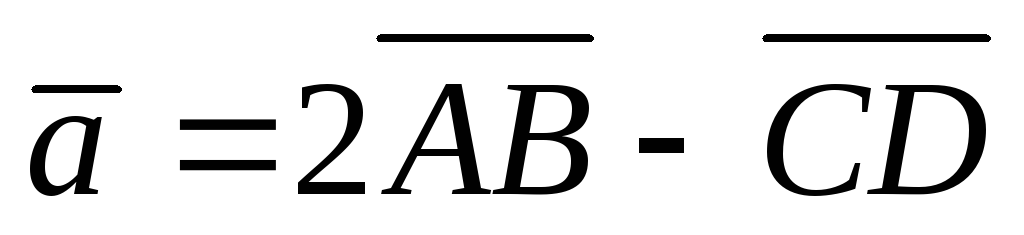 на направление вектора
на направление вектора
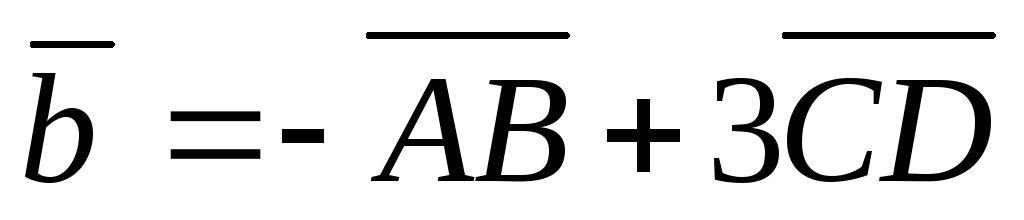 .
. -
Найти вектор
 ,
удовлетворяющий условиям
,
удовлетворяющий условиям
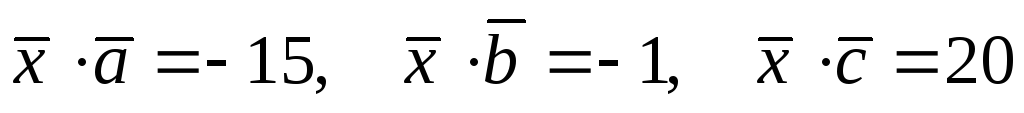 ,
если
,
если
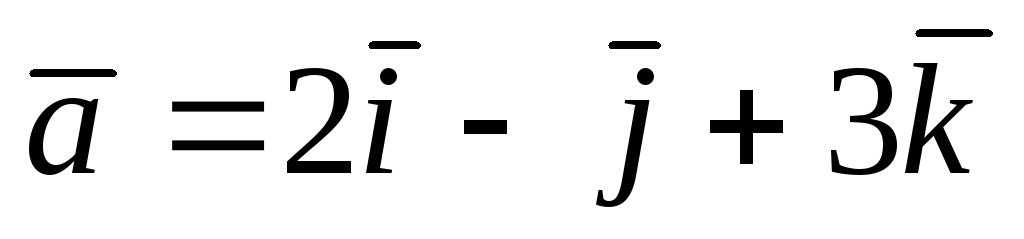 ,
,
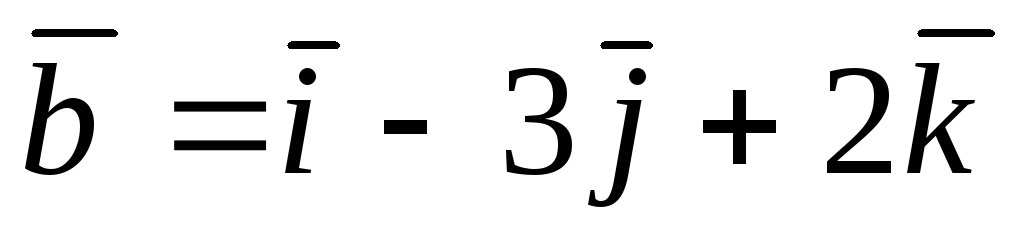 и
и
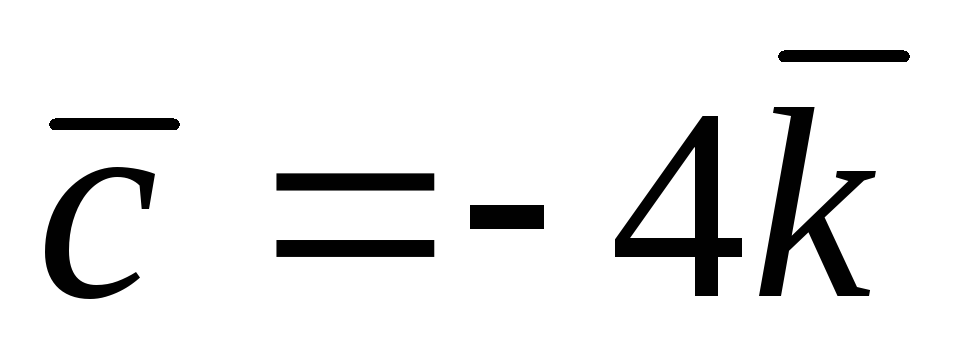 .
. -
Вектор составляет с осями
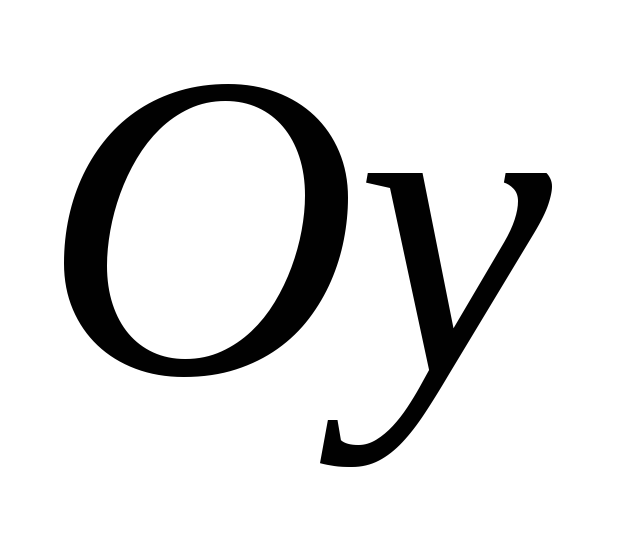 и
и
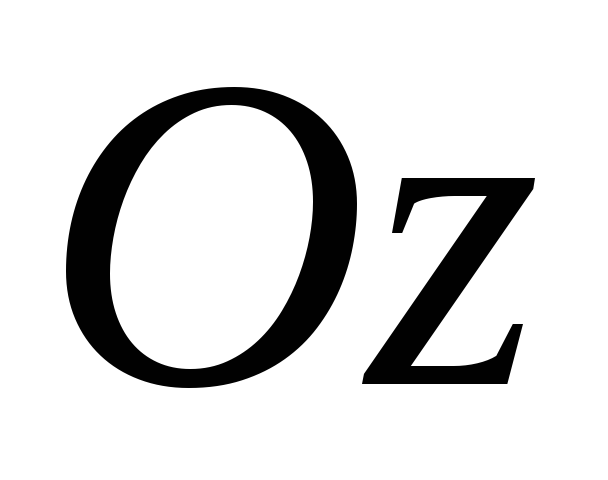 углы
углы
 и
и
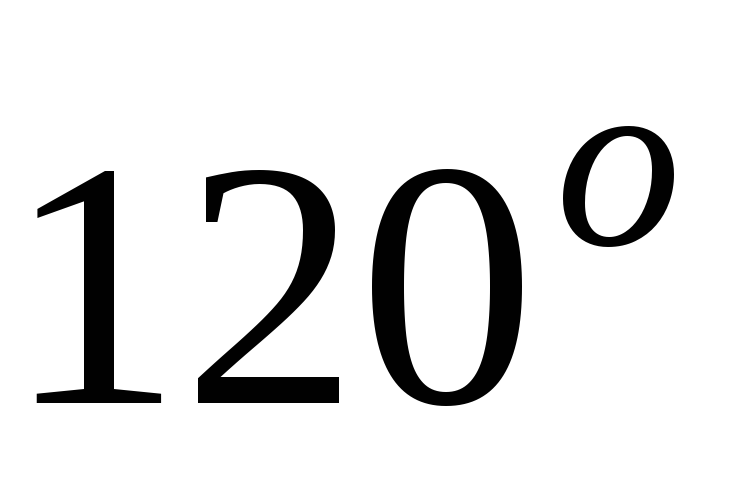 .
Какой угол он составляет с осью
.
Какой угол он составляет с осью
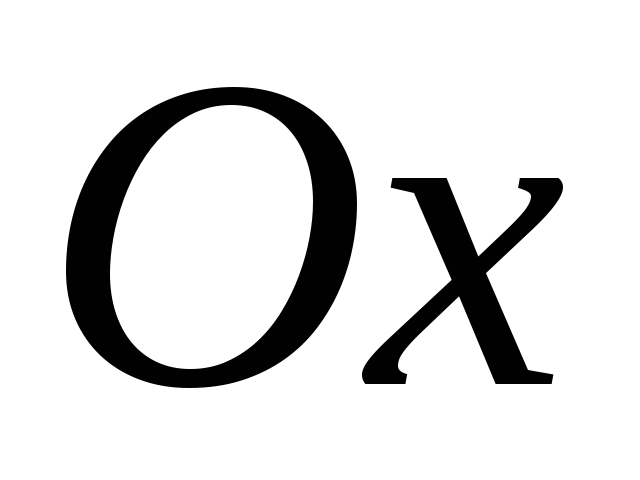 ?
? -
Коллинеарны ли векторы
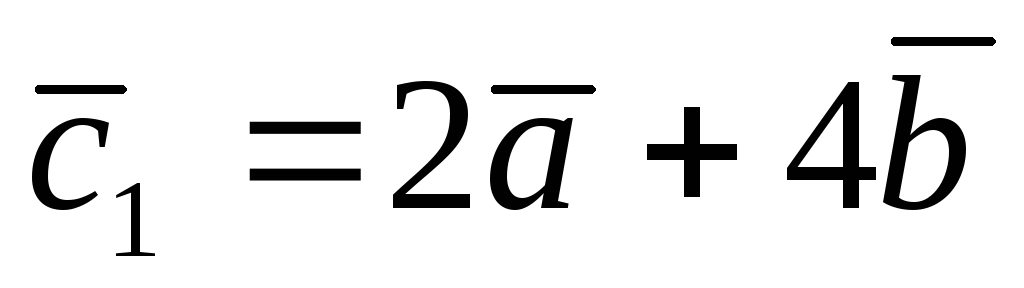 и
и
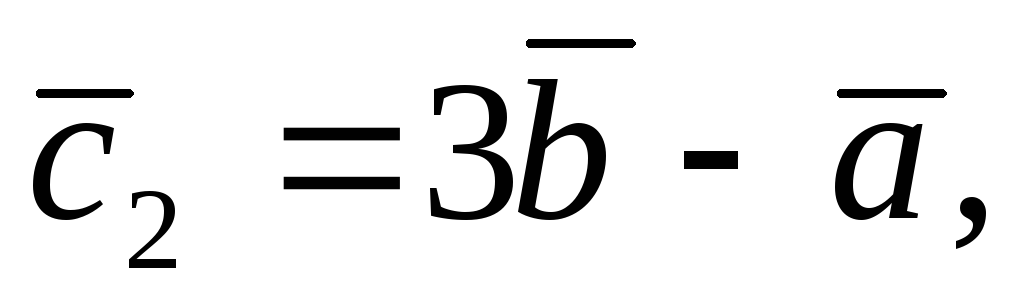 если
если
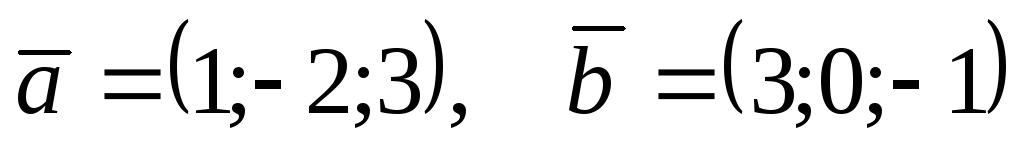 .
. -
Вычислить проекцию вектора
 на направление вектора
на направление вектора
 ,
если
,
если
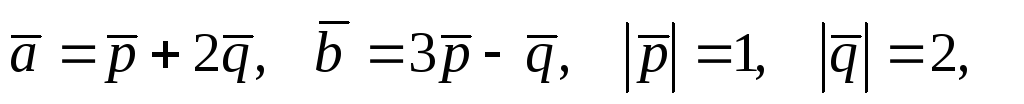 а
угол между векторами
а
угол между векторами
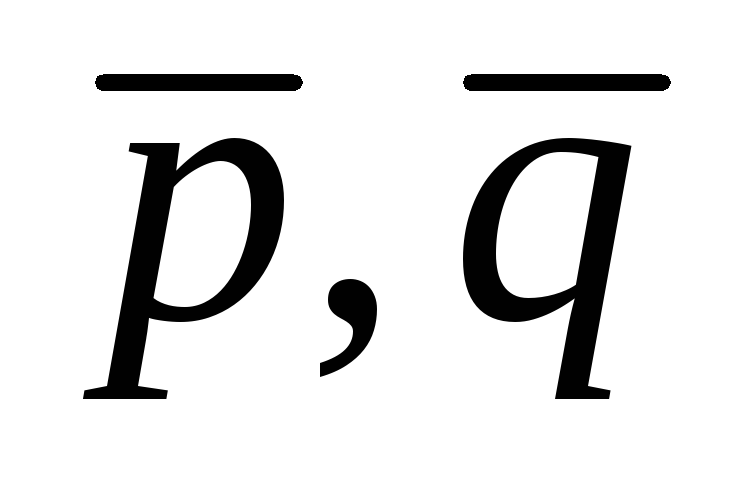 равен
равен
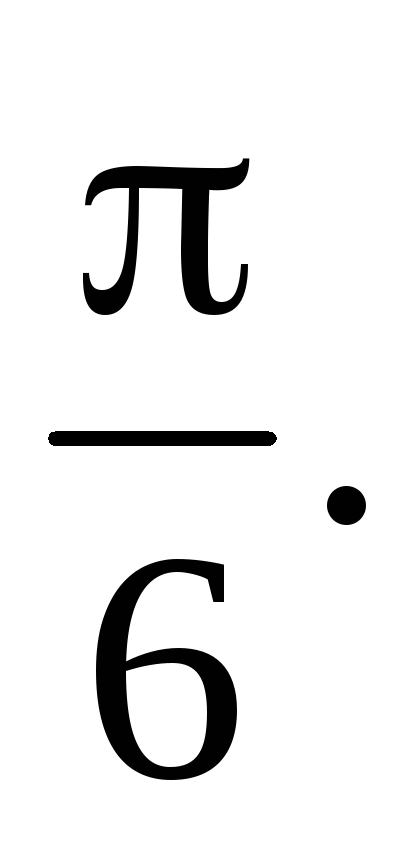
-
Найти вектор
 ,
перпендикулярный векторам
,
перпендикулярный векторам
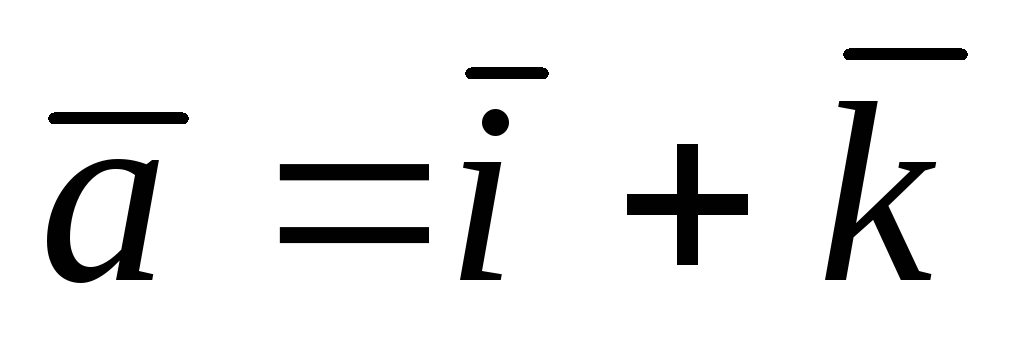 ,
,
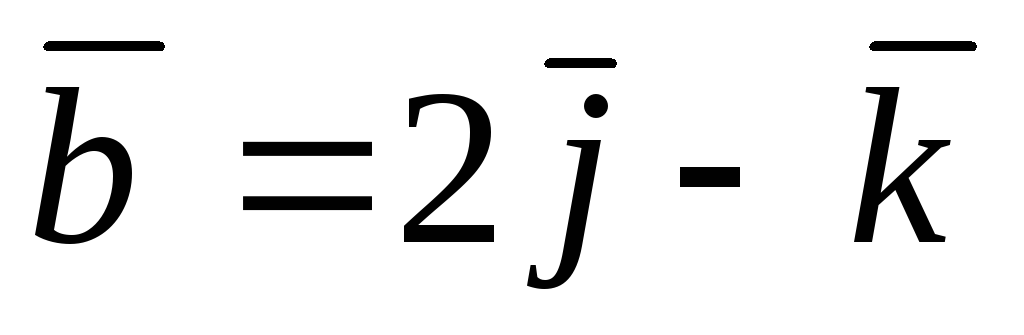 ,
если известно, что его проекция на
вектор
,
если известно, что его проекция на
вектор
 равна 1.
равна 1. -
Вектор
 составляет с осями координат острые
углы
составляет с осями координат острые
углы
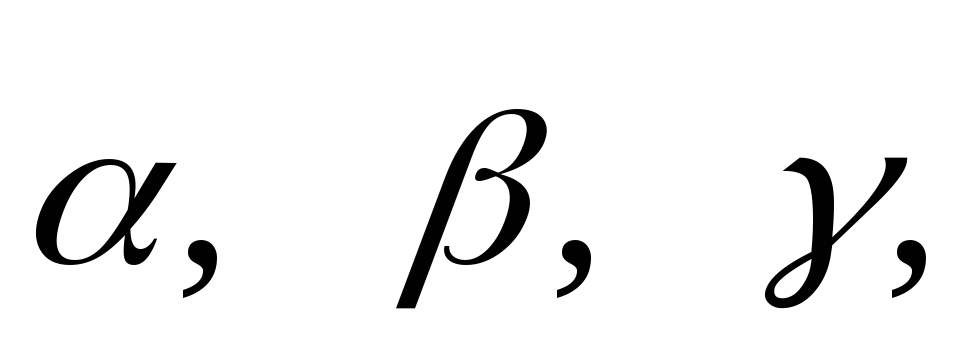
 причем
причем
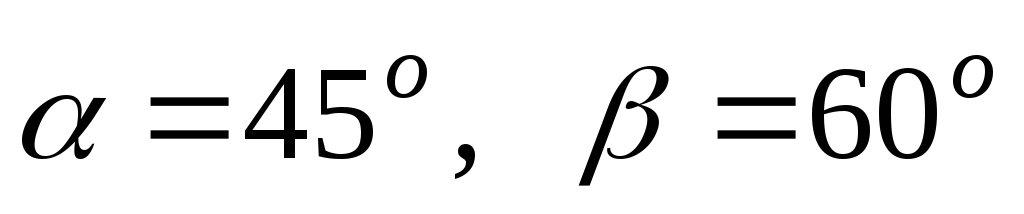 .
Найти его координаты, если
.
Найти его координаты, если
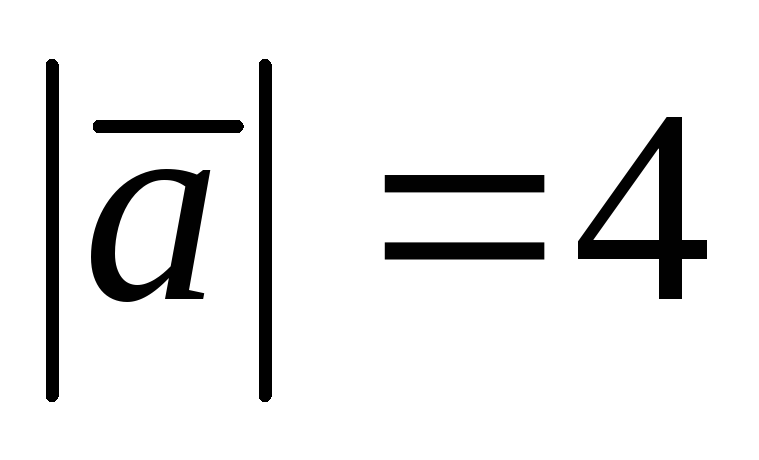 .
. -
Векторы
 и
и
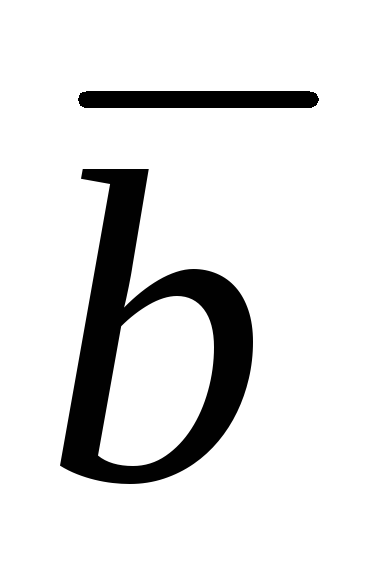 образуют угол
образуют угол
 ,
причем
,
причем
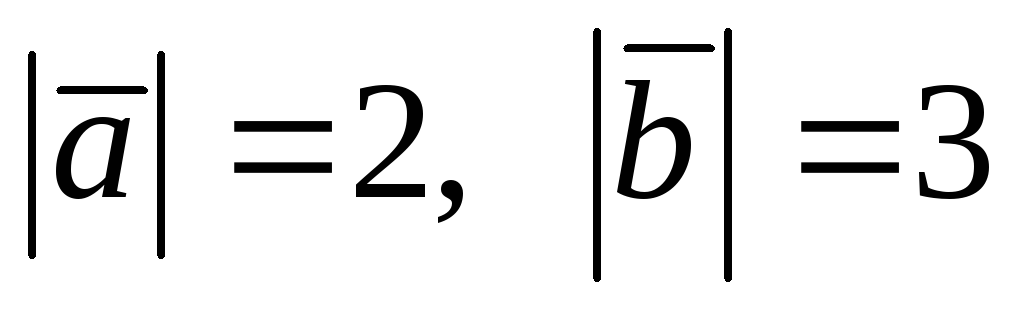 .
При каком значении
.
При каком значении
 векторы
векторы
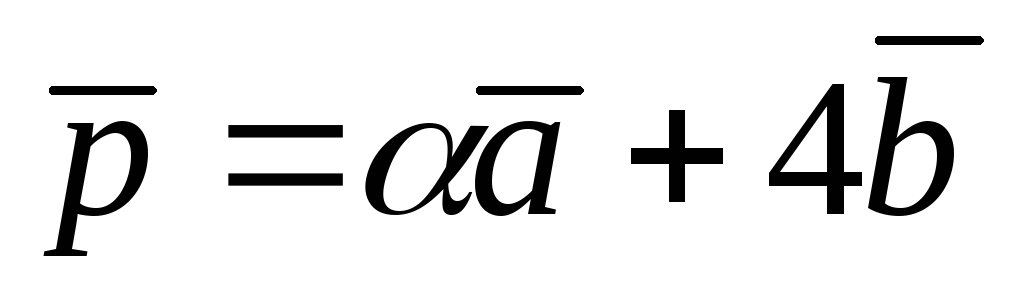 и
и
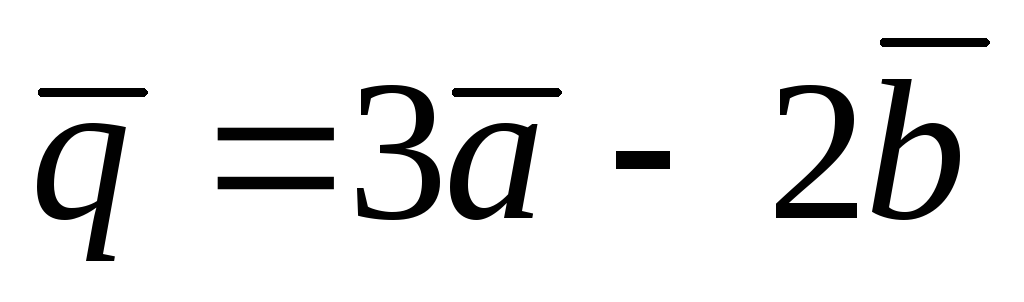 перпендикулярны?
перпендикулярны? -
Вектор
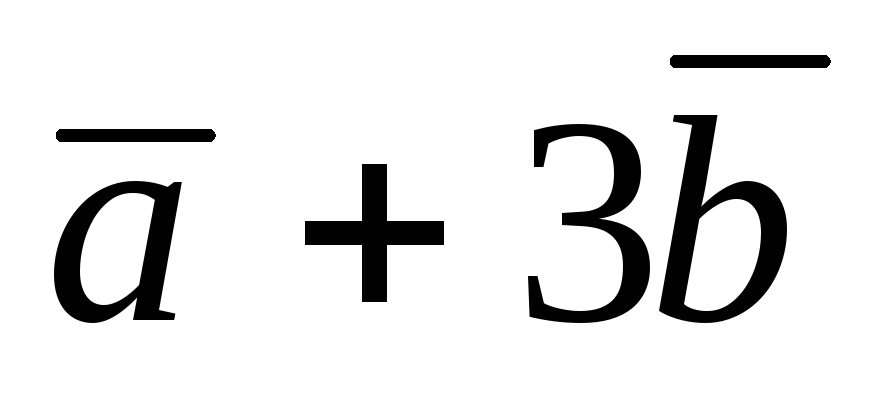 перпендикулярен к вектору
перпендикулярен к вектору
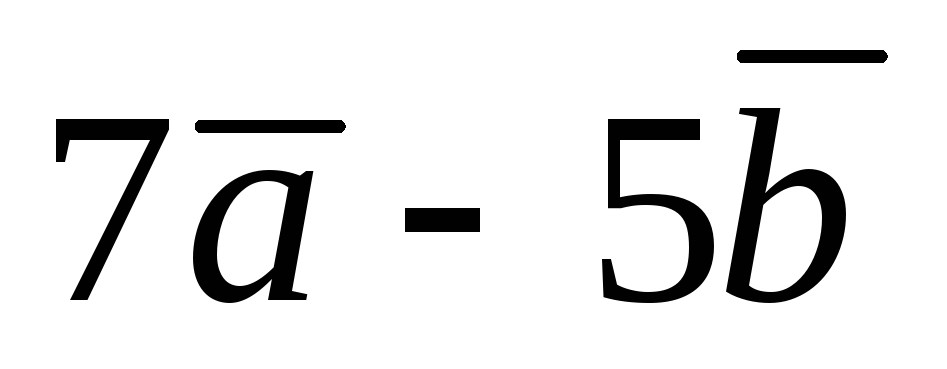 ,
а вектор
,
а вектор
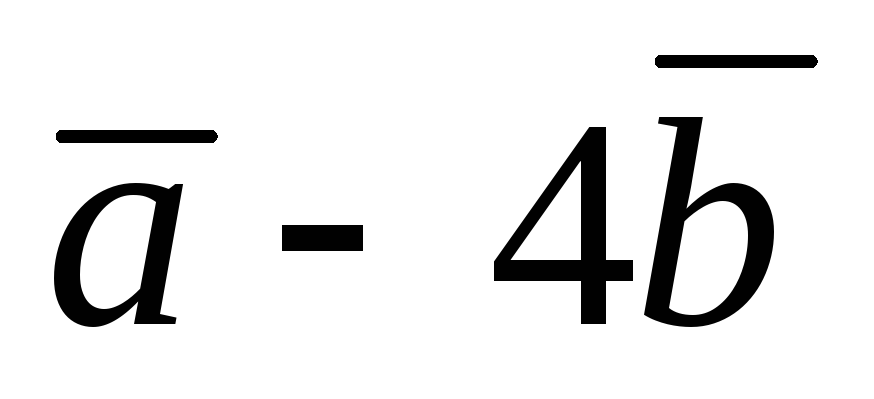 - к вектору
- к вектору
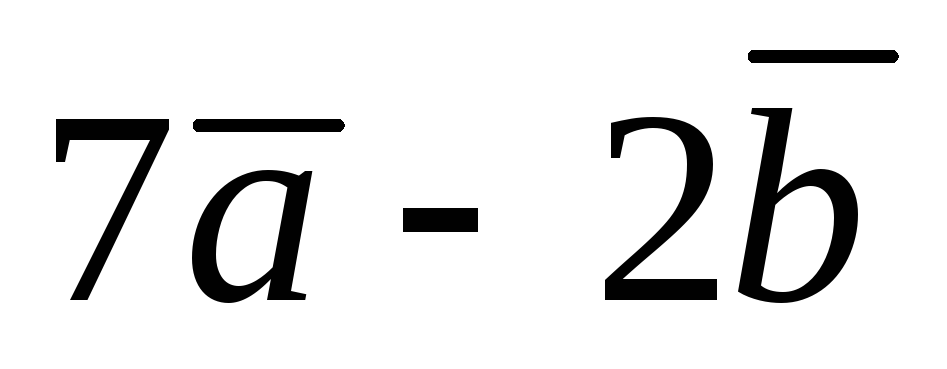 .
Определить угол между векторами
.
Определить угол между векторами
 и
и
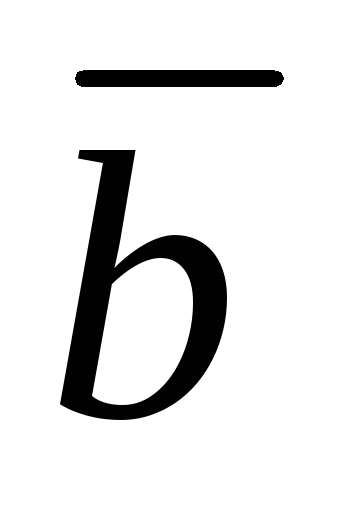 .
. -
Даны вершины треугольника А( -1; -2; 4), В( -4; -2; 0), С( 3; -2; 1). Найти орт медианы ВЕ.
-
Перпендикулярны ли векторы
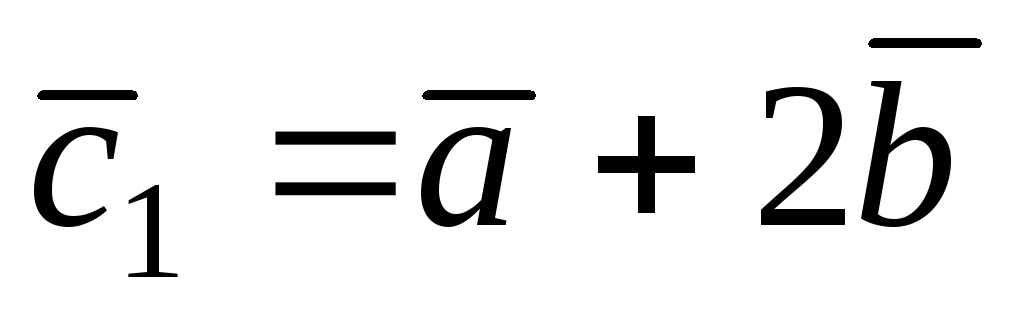 и
и
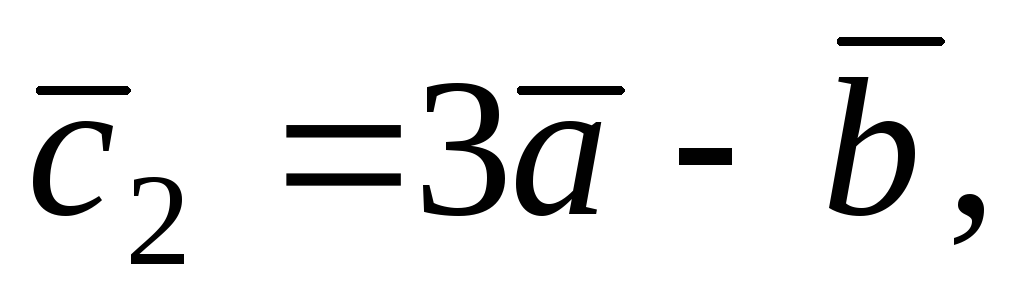 если
если
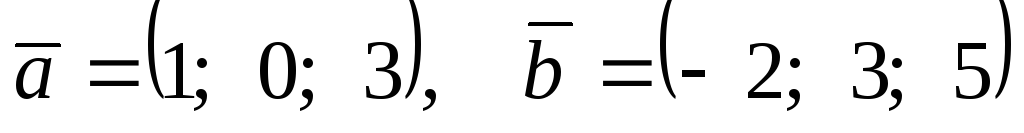 ?
?
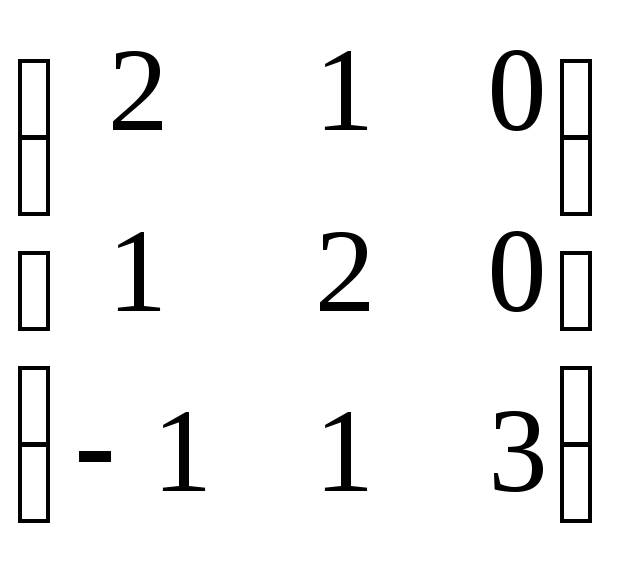
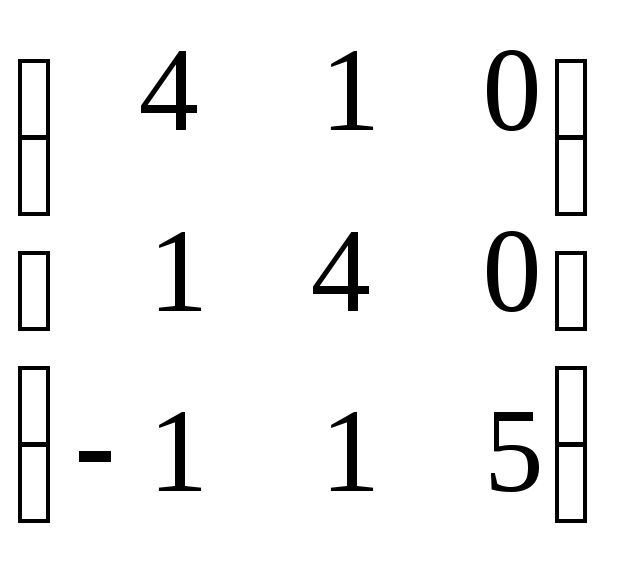
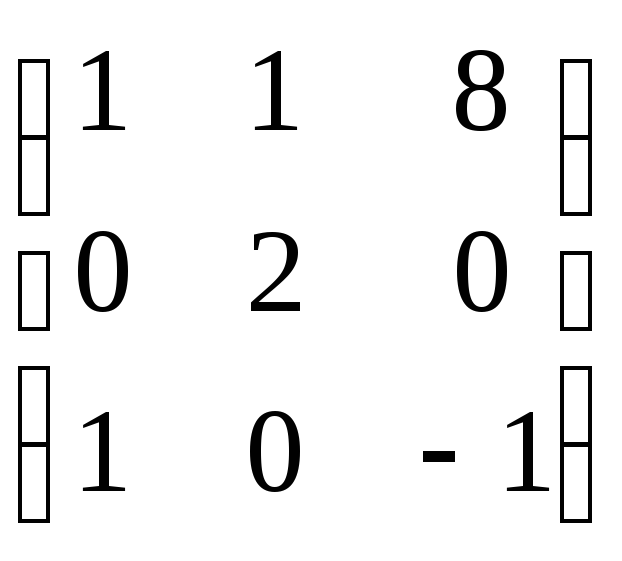
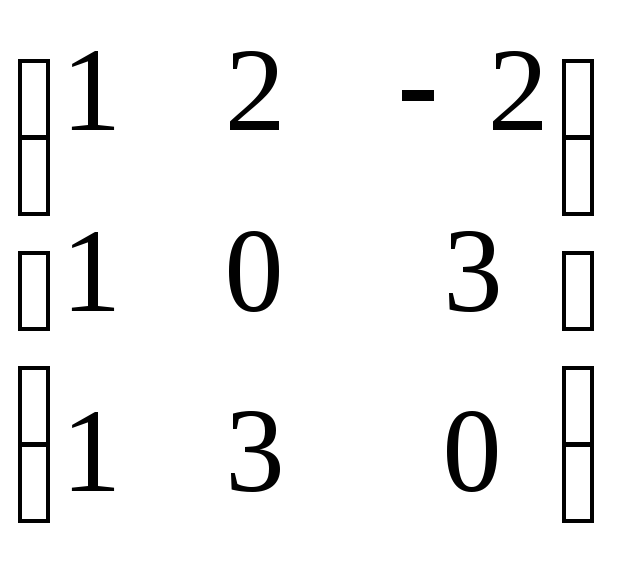
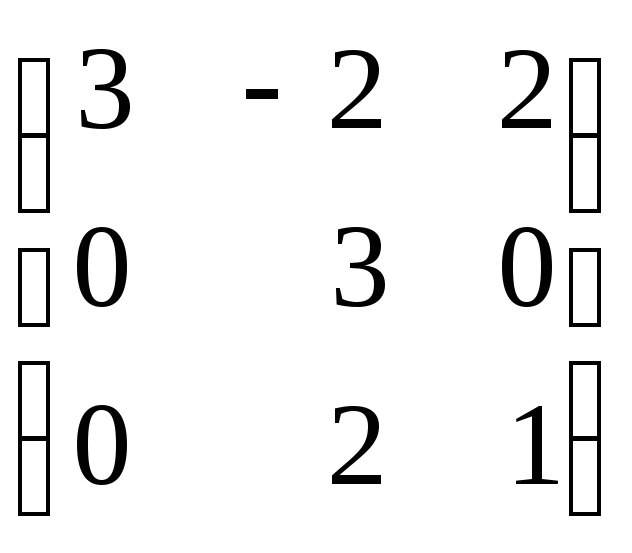
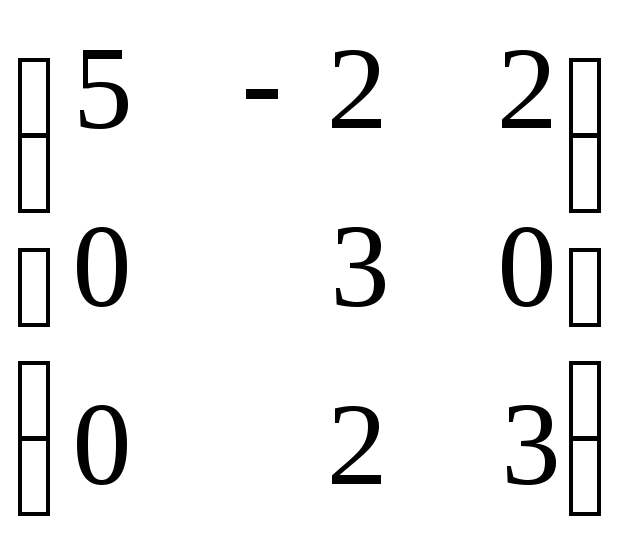
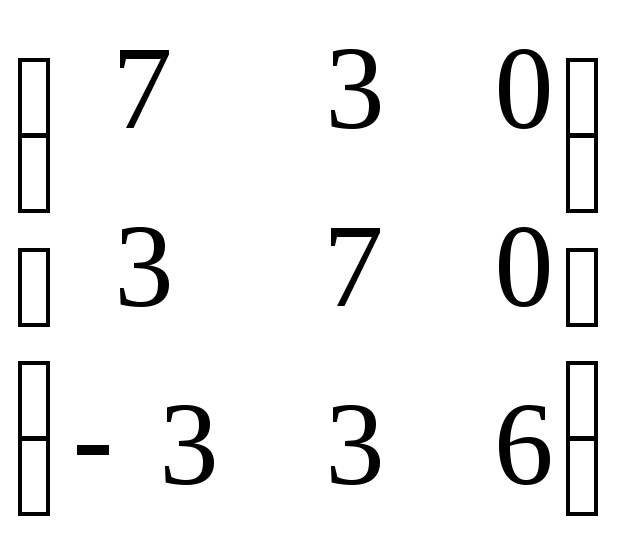
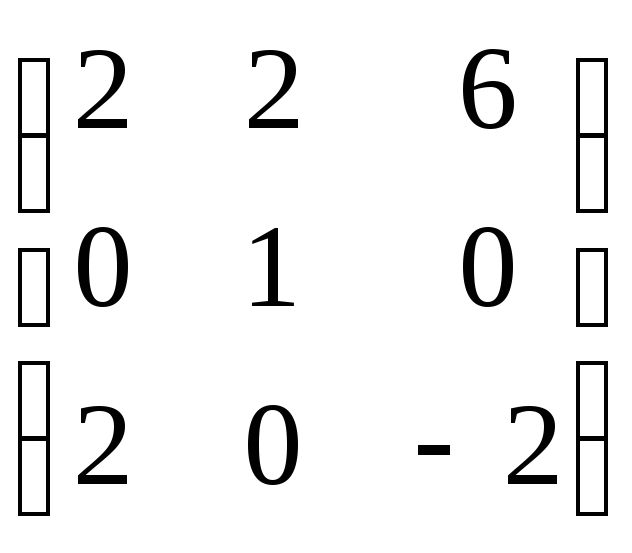
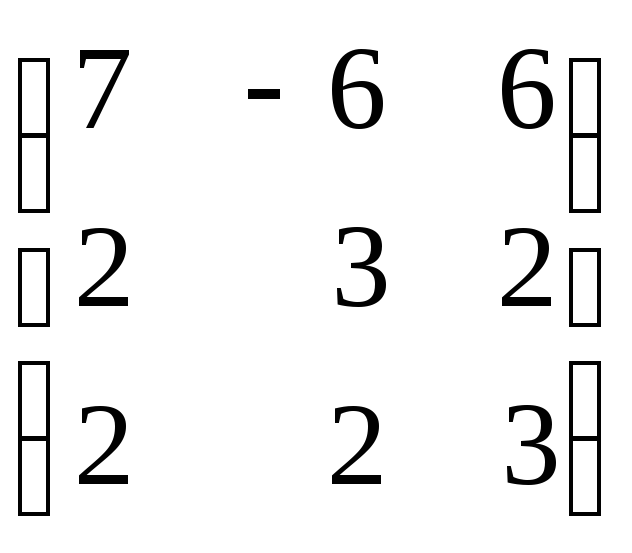
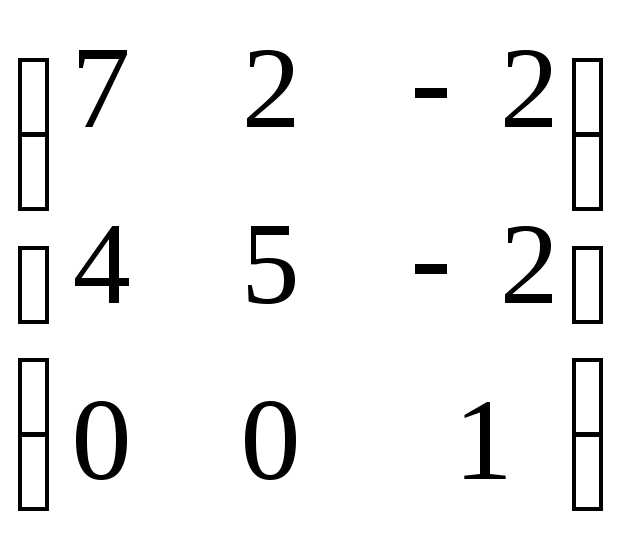
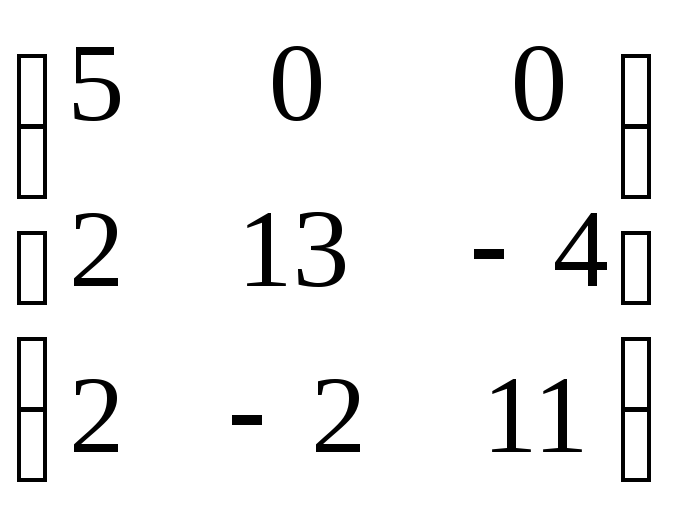
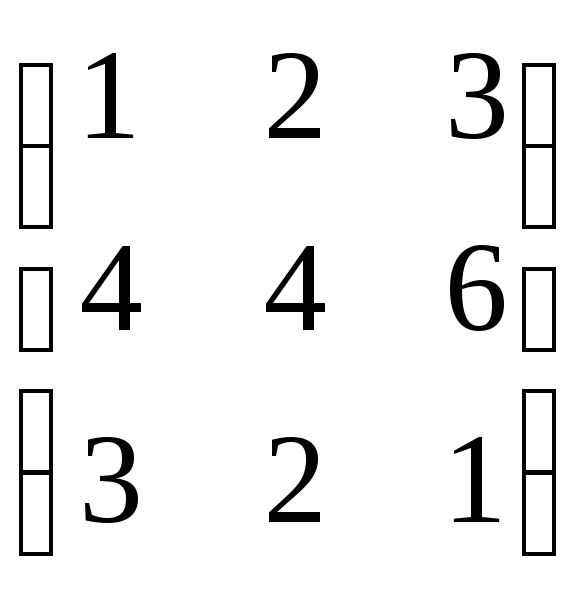
Задание 8. Найти собственные значения и собственные векторы матрицы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
|
|
|
|
|
|
|