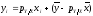- •Фізичний зміст задачі спільного зрівнювання декількох вимірюваних величин.
- •Методика оцінки точності за матеріалами зрівнювання.
- •Закони розподілу випадкових величин.
- •Математичний зміст задачі спільного зрівнювання декількох вимірюваних величин.
- •Математичне очікування дискретної і неперервної випадкової величини. Властивості математичного очікування.
- •Суть принципу найменших квадратів.
- •Дисперсія та середнє квадратичне відхилення (стандарт).
- •Основні шляхи розв’язання задачі зрівнювання.
- •Методика параметричного та корелатного способу зрівнювання.
- •Статистичні зв’язки. Властивості коефіцієнта кореляції.
- •Класифікація помилок вимірювання.
- •Статистична перевірка гіпотез.
- •Вплив помилок округлень аргументів на точність функції.
- •Методика обчислення коефіцієнтів нормальних рівнянь.
- •Систематичні помилки вимірів.
- •Найімовірніше значення багаторазового і рівноточно вимірювальної величини. Оцінка точності.
- •Способи розв’язання нормальних рівнянь.
- •Порядок обробки рівно точних вимірювань однієї величини.
- •Способи контролю розв’язання нормальних рівнянь.
- •Методика обчислень ваг функції.
- •Найімовірніше значення багаторазового і нерівноточно вимірювальної величини.
- •Порядок обробки нерівно точних вимірювань однієї величини.
- •Опис помилок точності по різницях подвійних рівно точних вимірювань.
- •Зміст коефіцієнту кореляції та його властивості.
- •Поняття апроксимації квадратичної функції (постановка задачі).
- •Методика оцінки емпіричного значення дисперсії.
- •Рівняння регресії.
- •Методика приведення рівнянь до рівноточного виду.
-
Зміст коефіцієнту кореляції та його властивості.
Коефіцієнт кореляції - це міра тісноти лінійного кореляційного зв’язку і обчислюється за формулою:
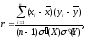

xi,yi – різні значення змінних, отримані зі спостережень.
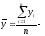 середнє
арифметичне величини
середнє
арифметичне величини
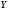

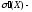 емпіричне
середнє квадратичне відхилення
емпіричне
середнє квадратичне відхилення
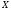
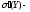 емпіричне
середнє квадратичне відхилення
емпіричне
середнє квадратичне відхилення
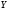

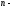 число
спостережень
число
спостережень
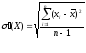
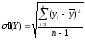
Властивості:
1)
коефіцієнт кореляції змінюється в межах
від -1 до +1, тобто
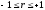
2)
коли коефіцієнт кореляції дорівнює +1
або -1, між
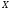 та
та
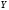 існують
точні прямолінійні зв’язки, тобто:
існують
точні прямолінійні зв’язки, тобто:
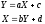
При
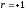 зі збільшенням або зменшенням
зі збільшенням або зменшенням
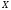 збільшується
або зменшується
збільшується
або зменшується
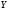 .
Коли
.
Коли
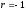 ,
зі збільшенням
,
зі збільшенням
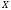 зменшується
зменшується
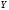 і
зі зменшенням
і
зі зменшенням
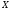 збільшується
збільшується
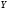 .
.
3)якщо
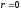 ,
то між
,
то між
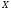 та
та
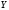 прямолінійного
кореляційного зв’язку не існує. Чим
ближче коефіцієнт кореляції
прямолінійного
кореляційного зв’язку не існує. Чим
ближче коефіцієнт кореляції
 до
=1 або -1, тим ближче кореляційний зв’язок
між змінними
до
=1 або -1, тим ближче кореляційний зв’язок
між змінними
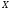 та
та
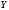 до
функціональної; чим ближче коефіцієнт
кореляції до 0, тим менш зв’язані між
собою змінні
до
функціональної; чим ближче коефіцієнт
кореляції до 0, тим менш зв’язані між
собою змінні
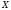 та
та
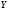 .
.
-
Поняття апроксимації квадратичної функції (постановка задачі).
Однією із задач, які розв`язує сучасна обчислювальна математика, є проблема наближення функції однієї змінної та багатьох дійсних змінних іншими функціями більш простої, взагалі кажучи будови, які легко обчислюються на електронно-обчислювальних машинах. Інша назва цієї задачі – апроксимування функції.
Припустимо,
що в результаті інженерного або наукового
експерименту отримана система точок
![]() .
Необхідно знайти аналітичну залежність
Q (х),
таку, яка найкращим чином описує задану
систему точок. Поняття "найкращим
чином" означає розв’язання задачі
по заданому критерію. Найбільш відомим
критерієм для задач апроксимації є
критерій середньоквадратичних відхилень
(СКВ), який являє собою мінімізацію суми
квадратів відхилень експериментальних
даних від аналітичної функції Q
(x)і
визначається на заданій множині точок
як
.
Необхідно знайти аналітичну залежність
Q (х),
таку, яка найкращим чином описує задану
систему точок. Поняття "найкращим
чином" означає розв’язання задачі
по заданому критерію. Найбільш відомим
критерієм для задач апроксимації є
критерій середньоквадратичних відхилень
(СКВ), який являє собою мінімізацію суми
квадратів відхилень експериментальних
даних від аналітичної функції Q
(x)і
визначається на заданій множині точок
як
![]()
Однак при такій постановці задача апроксимації експериментальних даних має багато розв’язків. Для отримання єдиного розв’язку цієї задачі потрібно задавати значення Q (x)певного вигляду, наприклад:
степеневим поліномом
![]()
тригонометричним поліномом
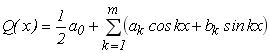
ортогональним поліномом
![]()
сплайн-функцією та інш.
-
Методика оцінки емпіричного значення дисперсії.
Нормальною оцінкою дисперсії служить її виморочна дисперсія.
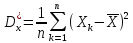
Для
розрахунку математичного очікування
та дисперсії цієї оцінки, то
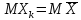 =mx,
представимо
у вигляді:
=mx,
представимо
у вигляді:
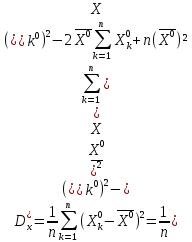
Тоді:
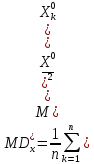
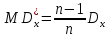
Для
вичислення дисперсії оцінки
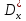 спочатку треба знайти її момент другого
порядку
спочатку треба знайти її момент другого
порядку
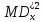
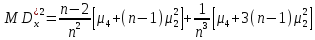 ,
,
Де
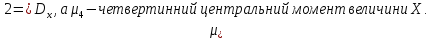
Після цього знаходимо:
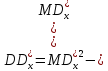
В результаті отримаємо оцінку
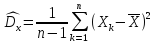
-
Рівняння регресії.
Для
виводу емпіричної формули, яка відображає
прямолінійний кореляційний зв’язок
між змінними
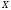 та
та
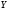 ,
застосовують рівняння
,
застосовують рівняння
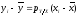 (1),
де
(1),
де
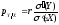 -
коефіцієнт регресії
-
коефіцієнт регресії
При прямолінійному кореляційному зв’язку між змінними існує рівняння регресії:
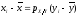 (2)
де
(2)
де
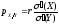 -
коефіцієнт регресії
-
коефіцієнт регресії
Середнє квадратичне відхилення коефіцієнтів регресії обчислюється так:
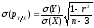
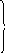
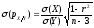
На практиці рівняння (1) слід привести до вигляду:
З
цієї формули видно, що коефіцієнт
регресії – це тангенс кута нахилу
прямої, а постійний доданок – це відрізок,
який відсікається цією прямою на осі
ординат.