17. Найімовірніше значення багаторазового і рівноточно вимірювальної величини. Оцінка точності.

Найімовірніше значення багаторазового і рівноточно вимірювальної величини.

З точки зору числових оцінок точності під рівноточними розуміють однорідні вимірювання, які характеризуються однаковою середньою квадратичною помилкою; при різних середньо квадратичних помилках однорідні вимірювання будуть нерівноточними. Нехай деяка величина, дійсне значення якої дорівнює X, виміряна рівноточно n раз і отримані результати: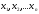. Потрібно знайти найбільш надійне значення виміряної величини, використовуючи дану сукупність (ряд) вимірів.

Ми знаємо, що точність шуканої величини характеризується: 1) відхиленням цієї величини від математичного сподівання результатів вимірювань 2) відхиленням математичного сподівання від істинного значення, обумовлене наявністю систематичних помилок у вимірах. Це відхилення не може бути зменшене

Залишається одне завдання: отримати найкраще наближення до математичного сподівання. Найкращим наближенням для ряду рівноточних результатів є середнім арифметичним цих результатів.

Тому як вірогідне значення для ряду равноточних результатів приймають середнє арифметичн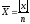е: , де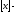 позначення суми, введене Гауссом

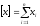
Алгебраїчну суму похідних у гауссовій позначенні записують:

Аналогічно:;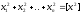

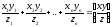
Основна властивість сум у гауссовому позначенні полягає в тому, що всі множники кожного доданка мають один і той же значок, тому суми творів виду 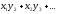в позначенні Гауса записані бути не можуть.

Оцінка точності вірогідного значення Під оцінкою точності розуміють встановлення довірчих меж для інтервалу, в якому ймовірно істинне значення вимірюваної величини. Для цього потрібно знати середню квадратичну помилку ймовірне значення. Позначимо через 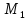середню квадратичну помилку середнього арифметичного рівноточних вимірювань при деякому постійному комплексі умов:

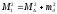
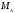
де - середнє квадратичне відхилення середнього арифметичного від математичного очікування для вимірюваної величини.

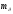- середня квадратична помилка математичного сподівання, що характеризує вплив на нього систематичних помилок при даному комплексі умов.

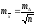з цього слідує

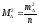
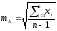де 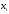– окреме вимірювання

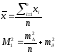
З останньої формули видно, що збільшення числа вимірів n буде ефективним лише до відомої межі.

18. Способи розв’язання нормальних рівнянь.

Розв’язання системи нормальних рівнянь є найбільш важкою частиною зрівнених обчислень. Існують різні способи розв’язання:

1)Спосіб Гаусса. Цей спосіб засновано на методі послідовного виключення невідомих, і він ввів зручну систему позначень, яка полегшує теоретичний розв’язок питань та запам’ятовування порядку дій; одноманітність послідовних дій та надійний контроль правильності проміжних результатів обчислень є великою перевагою . Цей спосіб називають алгоритмом Гауса і він є самим ефективним для розв’язку великих систем нормальних рівнянь.

2)Спосіб визначників має переваги лише при розв’язку двох рівнянь.

3)Спосіб краков’янів, який використовує можливості обчислюваних машин, особливо електроно-цифрових. Сутність цього метода у тому, що на обчислюваній машині отримуються без проміжних записів коефіцієнти рівнянь еквівалентної системи, поділені на корінь квадратний із квадратичних коефіцієнтів цих рівнянь.

4)при рішенні великого числа рівнянь, які розпадаються на частково-незалежні системи, може бути застосовано спосіб Праніс-Праневича.

5)спосіб обчислення на арифмометрі. При даному способі коефіцієнти перетворених рівнянь, які є сумами коефіцієнтів рівнянь та множення двох множників, можна отримати зразу на арифмометрі без проміжних записів. Тоді в схему розв’язання треба виписувати тільки коефіцієнти основних перетворених рівнянь. На арифмометрі обчислення досить точні, тому що обчислення можна проводити з більшою кількістю десяткових знаків та похибки округлення проміжних результатів не будуть впливати.

6)розв’язок рівнянь способом простої ітерації. Невеликі і добре обумовлені системи рівнянь (до 30 рівнянь) вигідно розв’язувати цим методом. Послідовність: Спочатку кожне невідоме виражають через ті, що залишились, користуючись тим рівнянням, в яке визначуване невідоме входить з квадратичним коефіцієнтом. Потім отримують ще одне значення кожного невідомого шляхом підстановки останніх значень невідомих в певні ітераційні рівняння.