
- •Контрольна робота №4 Зразок розв’язання і оформлення контрольної роботи №4
- •Завдання 4.3.31. Знайти загальний розв’язок диференціального рівняння другого порядку
- •Завдання 4.4.31. Знайти загальний розв’язок лінійного диференціального рівняння другого порядку
- •Завдання 4.2. Знайти розв’язок задачі Коші диференціального рівняння першого порядку:
- •Завдання 4.3. Знайти загальний розв’язок диференціального рівняння другого порядку:
- •Завдання 4.4. Знайти загальний розв’язок лінійного диференціального рівняння другого порядку:
Контрольна робота №4 Зразок розв’язання і оформлення контрольної роботи №4
Варіант № 31
Завдання 4.1.31. Розв’язати диференціальні рівняння:
а)
![]() ,
б)
,
б)
![]() .
.
Розв’язання.
а)
Рівняння
![]() є рівнянням з відокремлюваними змінними.
є рівнянням з відокремлюваними змінними.
Для
відокремлення змінних, поділимо обидві
частини рівняння на добуток
![]() ,
в результаті чого отримаємо диференціальне
рівняння
,
в результаті чого отримаємо диференціальне
рівняння
![]() .
.
Інтегруємо останнє рівняння
![]() ,
,
![]() ,
,
![]() - загальний
інтеграл заданого рівняння.
- загальний
інтеграл заданого рівняння.
б)
Рівняння
![]() записане в загальній формі. Виразимо з
нього
записане в загальній формі. Виразимо з
нього
![]() і отримаємо рівняння в нормальній формі
і отримаємо рівняння в нормальній формі
![]() .
.
Це рівняння є однорідним диференціальним рівнянням. Дійсно,
![]() .
.
Для
розв’язання однорідного рівняння
введемо заміну
![]() ,
тоді
,
тоді
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
Повертаючись до
змінної
![]() ,
знаходимо загальний інтеграл
заданого
рівняння:
,
знаходимо загальний інтеграл
заданого
рівняння:
![]() або
або
![]() .
.
Завдання 4.2.31. Знайти розв’язок задачі Коші лінійного диференціального рівняння першого порядку
![]() .
.
Розв’язання. Задача Коші полягає в тому, щоб визначити частинний розв’язок диференціального рівняння, використовуючи для цього початкову умову. Для цього спочатку знаходимо загальний розв’язок диференціального рівняння.
Задане
рівняння є лінійним (![]() і
і
![]() містяться
в рівнянні лише в перших степенях).
Розв’язуємо його методом Бернуллі. За
формулою маємо
містяться
в рівнянні лише в перших степенях).
Розв’язуємо його методом Бернуллі. За
формулою маємо
![]() ,
,
![]() .
.![]()
![]() ,
,
![]() .
.
Складаємо систему двох рівнянь:
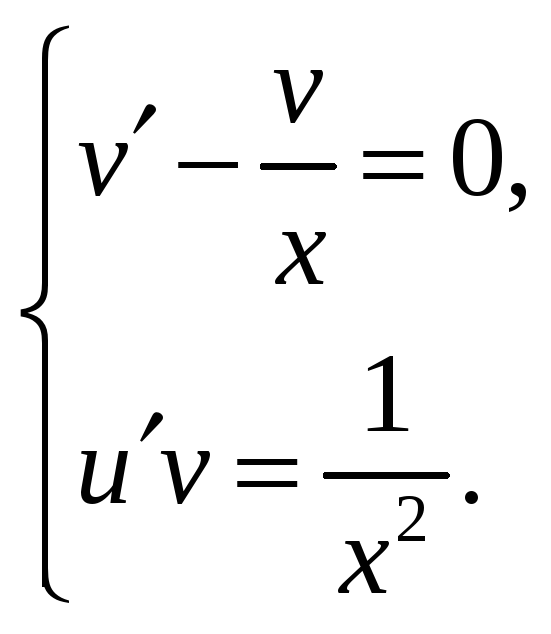
Розв’язуємо перше з рівнянь системи:
![]()
![]()
![]() ,
,
![]() .
.
Підставляємо
отримане значення функції
![]() в друге рівняння системи і розв’язуємо
його:
в друге рівняння системи і розв’язуємо
його:
![]()
![]()
![]() ,
,
![]() .
.
Запишемо загальний розв’язок диференціального рівняння
![]() .
.
Для
розв’язання
задачі Коші застосуємо початкову умову
і знайдемо значення сталої
![]() ,
для чого підставимо в загальний розв’язок
значення
,
для чого підставимо в загальний розв’язок
значення
![]() ,
,
![]() :
:
 .
.
Отже, частинний розв’язок диференціального рівняння має вигляд
![]() .
.
Завдання 4.3.31. Знайти загальний розв’язок диференціального рівняння другого порядку
![]() .
.
Розв’язання.
Рівняння
другого порядку
![]() є
диференціальним
рівнянням
, яке не містить шуканої функції
є
диференціальним
рівнянням
, яке не містить шуканої функції
![]() .
.
Покладемо
![]() .
Тоді
.
Тоді
![]() і задане рівняння набуває вигляду
і задане рівняння набуває вигляду
![]() або
або
![]() .
.
Отримане рівняння є рівнянням з відокремлюваними змінними. Відокремлюючи змінні, отримаємо рівняння
![]() ,
,
проінтегрувавши яке маємо:
![]()
![]()
![]()
![]() або
або
![]() .
.
Розв’язуємо останнє рівняння та отримуємо загальний розв’язок диференціального рівняння
![]() .
.
Завдання 4.4.31. Знайти загальний розв’язок лінійного диференціального рівняння другого порядку
![]() .
.
Розв’язання.
Задане рівняння є лінійним неоднорідним
рівнянням другого порядку зі сталими
коефіцієнтами. Згідно з формулою
загальний розв’язок лінійного
неоднорідного диференціального рівняння
складається із загального розв’язку
![]() відповідного однорідного рівняння
відповідного однорідного рівняння
![]() і
деякого частинного розв’язку
і
деякого частинного розв’язку
![]() лінійного неоднорідного рівняння:
лінійного неоднорідного рівняння:
![]() .
.
Знайдемо
спочатку
![]() .
Для цього складемо характеристичне
рівняння і знайдемо його корені:
.
Для цього складемо характеристичне
рівняння і знайдемо його корені:
![]() ,
,
![]() .
.
Загальний розв’язок однорідного рівняння знаходимо за формулою:
![]() .
.
Далі
визначаємо
![]() .
В нашому випадку права частина
диференціального рівняння має вигляд
.
В нашому випадку права частина
диференціального рівняння має вигляд
![]() ,
,
де
![]() ,
тобто число
,
тобто число
![]() є двократним коренем характеристичного
рівняння. Отже, частинний розв’язок
неоднорідного рівняння будемо шукати
у вигляді
є двократним коренем характеристичного
рівняння. Отже, частинний розв’язок
неоднорідного рівняння будемо шукати
у вигляді
![]() ,
,
де
![]() - невідомий коефіцієнт. Знайдемо
- невідомий коефіцієнт. Знайдемо
![]() ,
,
![]()
Підставимо
знайденні похідні в рівняння
![]() :
:![]()
![]()
Тотожно прирівнявши ліву і праву частини останнього рівняння, знайдемо
![]()
![]() .
.
Таким
чином,
![]() - частинний розв’язок
лінійного неоднорідного диференціального
рівняння, а його загальний розв’язок
має вигляд
- частинний розв’язок
лінійного неоднорідного диференціального
рівняння, а його загальний розв’язок
має вигляд
![]() .
.
Завдання 4.5.31. Дослідити на збіжність числові ряди
а)
![]()
Розв’язання.
Запишемо
![]() -ий
і
-ий
і
![]() -ий
члени заданого ряду:
-ий
члени заданого ряду:
![]() .
Тепер застосуємо ознаку Даламбера:
.
Тепер застосуємо ознаку Даламбера: .
.
![]() ,
отже досліджуваний ряд збігається.
,
отже досліджуваний ряд збігається.
б)
![]() .
.
Розв’язання. За радикальною ознакою Коші
![]() ,
,
![]() ,
тому
цей ряд збіжний.
,
тому
цей ряд збіжний.
в)
![]()
Розв’язання.
Порівняємо цей ряд зі збіжною геометричною
прогресією:
![]() ,
знаменник якої
,
знаменник якої
![]() .
Оскільки при всіх
.
Оскільки при всіх
![]() маємо:
маємо:
![]() ,
то за
ознакою
порівняння досліджуваний ряд
- збіжний.
,
то за
ознакою
порівняння досліджуваний ряд
- збіжний.
г)
![]() , де
, де
![]() -
деяка
стала.
-
деяка
стала.
Розв’язання.
Використаємо
інтегральну ознаку збіжності, беручи
в якості
![]() :
:
![]() .
Якщо
.
Якщо
![]() ,
то
,
то
![]() ,
тобто
інтеграл, а разом з ним і ряд – розбіжні.
Якщо
,
тобто
інтеграл, а разом з ним і ряд – розбіжні.
Якщо
![]() ,
то
,
то
![]()
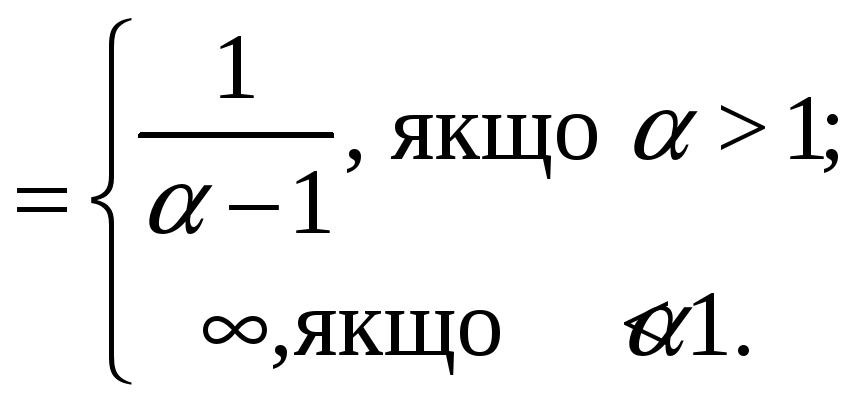
Отже, узагальнений
гармонічний ряд
![]() збігається, коли
збігається, коли
![]() ,
і розбігається, коли
,
і розбігається, коли
![]() .
.
Завдання 4.6.31. Дослідити на абсолютну та умовну збіжність знакозмінний числовий ряд:
а)

Розв’язання. Обидві умови ознаки Лейбніца виконані, тому ряд - збіжний. Запишемо ряд з абсолютних величин членів заданого ряду:
![]()
Застосуємо для
цього ряду інтегральну ознаку Коші,
взявши
![]() .
.
Маємо:
![]()
За інтегральною ознакою Коші останній ряд збіжний, отже заданий ряд - абсолютно збіжний.
б)
![]() де
де
![]() - деяка стала.
- деяка стала.
Розв’язання. Маємо знакозмінний ряд. Розглянемо збіжність ряду, складеного з абсолютних величин членів заданого ряду:
![]() .
.
Порівняємо
![]() ий
член цього ряду з
ий
член цього ряду з
![]() м
членом
узагальненого гармонічного ряду
м
членом
узагальненого гармонічного ряду
![]() :
:
 .
.
Вище було доведено,
що узагальнений гармонічний ряд
![]() збігається, якщо
збігається, якщо
![]() В нашому випадку
В нашому випадку
![]() отже за ознакою порівняння збігається
ряд з абсолютних величин, а заданий ряд
-
абсолютно
збіжний.
отже за ознакою порівняння збігається
ряд з абсолютних величин, а заданий ряд
-
абсолютно
збіжний.
Завдання 4.7.31. Розкласти в ряд Маклорена функції:
а)
![]() .
.
Розв’язання.
Користуючись формулою зниження степеня,
маємо:
![]() .
Степеневий ряд для
.
Степеневий ряд для
![]() можна отримати з ряду
можна отримати з ряду
![]() ,
якщо брати в цьому ряді
,
якщо брати в цьому ряді
![]() замість
замість
![]() :
:
![]() .
.
Отже,
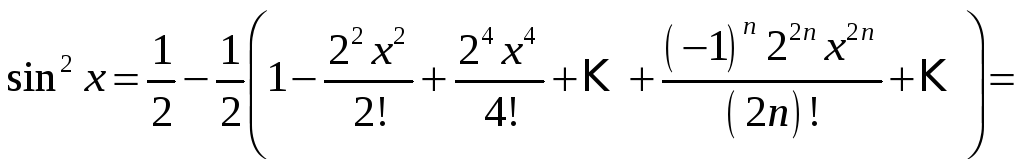
![]()
б)
![]() .
.
Розв’язання. Скористаємося біноміальним рядом:

Ряд функції
![]() отримуємо з цього ряду заміною
отримуємо з цього ряду заміною
![]() на
на
![]() :
:

Тоді :
![]()
![]() .
Оскільки цей ряд отриманий з біноміальною
заміною
.
Оскільки цей ряд отриманий з біноміальною
заміною
![]() на
на
![]() ,
то він буде
збіжним при
,
то він буде
збіжним при
![]() або
або
![]() .
.
ВАРІАНТИ ЗАВДАНЬ КОНТРОЛЬНОЇ РОБОТИ № 4
Завдання 4.1. Розв’язати диференціальні рівняння:
|
4.1.1.a) |
б) |
|
4.1.2.a) |
б) |
|
4.1.3.
a) |
б) |
|
4.1.4.
a) |
б) |
|
4.1.5. a) |
б) |
|
4.1.6.
a) |
б) |
|
4.1.7.a) |
б) |
|
4.1.8.a) |
б) |
|
4.1.9.
a) |
б) |
|
4.1.10.
a)
|
б) |
|
4.1.11.a)
|
б) |
|
4.1.12. a) |
б) |
|
4.1.13. a)
|
б) |
|
4.1.14. a) |
б) |
|
4.1.15. a) |
б) |
|
4.1.16.
a) |
б) |
|
4.1.17. a) |
б) |
|
4.1.18.
a) |
б) |
|
4.1.19.a) |
б) |
|
4.1.20.
a) |
б) |
|
4.1.21.a)
|
б) |
|
4.1.22.a) |
б) |
|
4.1.23. a) |
б) |
|
4.1.24. a) |
б)
|
|
4.1.25. a) |
б) |
|
4.1.26.
a) |
б) |
|
4.1.27.a) |
б) |
|
4.1.28.a) |
б) |
|
4.1.29.
a)
|
б) |
|
4.1.30. a) |
б)
|
