Демонстрационный вариант контрольной работы.

Задание №1. Даны координаты вершин пирамиды А₁А₂А₃А₄ : А₁(1;2;1), А₂(3;-1;7), А₃(2;0;2), А₄(7;4;-2).. Требуется найти: 1) длину ребра А₁А₂; ₂) угол между ребрами А₁А₂ и А₁А₄; 3) угол между ребром А₁А₄ и гранью А₁А₂А₃; 4) площадь грани А₁А₂А₃; 5) объем пирамиды.

Решение:

1. Находим координаты вектора и длину ребра

2. Угол между ребрами А₁А₂ и А₁А₄ вычисляется по формуле

из скалярного произведения. =

Поэтому:

3. Угол между ребром А₁А₄ и плоскостью А₁А₂А₃ – это угол между вектором и его ортогональной проекцией А₁А₄` на грань А₁А₂А₃.

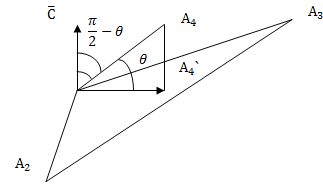
Вектор перпендикулярен грани А₁А₂А₃, что вытекает из определения векторного произведения векторов :

(Здесь . Как и в предыдущем пункте , находим

4. Площадь грани А₁А₂А₃ находим, используя смысл векторного произведения:

5.Объем пирамиды А1А2А3А4 численно равен одной шестой модуля смешанного произведения векторов .

Задание №2.

В кубе АBCDA₁B₁C₁D₁ со стороной a точка К является серединой стороны основания В₁С₁, точка L делит другую сторону C₁D₁ этого основания в отношении 2:1, считая от вершины С₁, точка N является серединой бокового ребра АА₁. Найдите площадь сечения, проходящего через точки К, L,N.

Решение:

Построим сечение куба через точки K, L, N.

(A₁B₁C₁) KL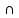 A₁D₁ = Q, (AA₁D₁) NQ DD₁=T, (BB1C) KG TN, NTLKG – искомое сечение. Площадь сечения вычислим, используя формулу ­­­­­­угол между нормальными векторами плоскости основания куба и плоскости сечения. Площадь проекции сечения куба на плоскостьABC можно вычислить как В декартовой системе координат с центром в вершине кубаA координаты вершин имеют вид: KОтсюда . Нормальный векторсечения можно принять пропорциональным (коллинеарным) векторному произведению.

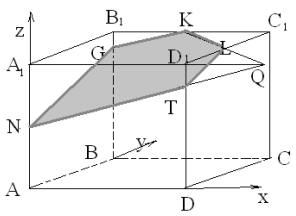
= (-4;-3;10). Нормальный вектор плоскости основания 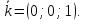Тогдаи

Ответ:

Задание №3.

Даны координаты вершин параллелепипеда: A(1;2;3), B(0;1;2), C(1;1;3), D(0;0;3). Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС.

Решение: По определению, объем параллелепипеда равен смешанному произведению векторов, на которых он построен. Найдем эти векторы:

.

Объем этого параллелепипеда .

С другой стороны, объем параллелепипеда ,- это площадь параллелограмма:.

, тогда высота .

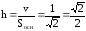Угол между вектором и гранью найдем по формуле

.

Так как вектор перпендикулярен грани, в которой лежат векторы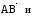. Угол между этим вектором и вектором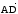находим по известной формуле

. Очевидно, что искомый угол .

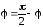Итак: .

Задание №4.

Проверить, лежат ли в одной плоскости точки ,. Найти линейную зависимость вектора, если это возможно.

Решение: Найдем три вектора: .

.

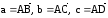Три вектора лежат в одной плоскости, если они компланарны, т. е. их смешанное произведение равно нулю: . Следовательно, эти три вектора линейно зависимы. Найдем линейную зависимостьот.

.

Решая эту систему, получим ответ: , т.е..

Задание 5.

В параллелепипеде АВСDА₁В₁С₁D₁ точка М — середина диагонали А₁С₁ грани A₁B₁C₁D₁, точка K — середина ребра ВВ₁. Докажите, что прямые А₁В₁, KМ и ВС₁параллельны некоторой плоскости.

Решение: Введем векторы:

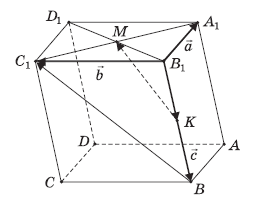
Тройку некомпланарных векторов примем в качестве базиса. Разложим векторы   по векторам этого базиса.

Имеем: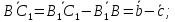 

Тогда

Это означает, что векторы   компланарны, следовательно, они параллельны некоторой плоскости, тогда этой плоскости параллельны и прямые А₁В₁, KМ и ВС₁, для которых векторы являются направляющими.

Задание №6

В кубе , ребро которого равно 6, найдите:

а) расстояние от вершины до плоскости

б) угол между диагональю грани и плоскостью

Решение:

 а) Пусть отрезок 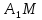— перпендикуляр из вершины на Тогда=. Найдем длину отрезка.

По правилу треугольника имеем: 

Обозначим: =, a в плоскости введем базисгде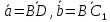и запишем разложение векторапо векторам этого базиса в виде:=

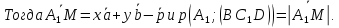
Так как (по определению прямой, перпендикулярной плоскости), значит,

Коэффициенты x и y в разложении векторанайдем, пользуясь условием:, которое равносильно системе уравнений

(, прежде чем решать эту систему уравнений, найдем скалярные произведения векторов:.

Так как треугольники - правильные и равные, то длины их сторон равны.

Тогда:

Вернемся к решению системы уравнений (. Учитывая соотношения (и свойства скалярного произведения векторов, получаем:

Тогда

Таким образом,

б) Обозначим Так какортогональная проекцияна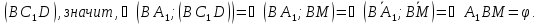

Используя соотношения(**) и (***) и то, что вектор приимеет вид

Ответ: а)

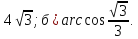
Задание №7.

 Найдите расстояние между скрещивающимися диагоналями АВ₁ и ВС₁ смежных граней АА₁В₁В и ВВ₁С₁С куба ABCDA₁B₁C₁D₁, если ребро этого куба равно 12.

Решение:

Введем векторы:  Тройку некомпланарных векторов примем в качестве базиса и разложим векторы по векторам этого базиса. Имеем: по векторам этого. Имеем: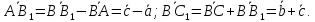

Пусть отрезок MH – общий перпендикуляр прямых AB₁ и BC₁ (. Тогда длина отрезкаравна расстоянию между этими прямыми:

Так как точка H лежит на диагонали коллинеарны, поэтому существует такое числоx, что .

Аналогично, в силу коллинеарности векторов .

По правилу ломанной находим:

Значения x и y найдем из условия:

Учитывая, что базисные векторы попарно взаимно перпендикулярны и длина каждого из них равна 12, имеем:

Получаем:

Таким образом, система векторных неравенств (1) равносильна системе уравнений

Тогда

Значит,

Ответ:

Задание №8

В треугольной пирамиде РАВС все плоские углы при вершине Р прямые. Найдите площадь сферы, описанной около этой пирамиды, если РА = 2, РВ = 3, РС = 4.

Решение: Пусть точка О — центр сферы, описанной около тетраэдра РАВС, R — радиус этой сферы. Тогда ОА = ОВ = ОС = ОР = R.

Введем некомпланарные векторы и примем их в качестве базисных в пространстве. Тогда при этом  Найдем коэффициенты х, у и z в этом разложении вектора 

По правилу треугольника имеем: 

откуда 

Из равенств ОА = ОВ = ОС = ОР (как радиусы сферы, описанной около тетраэдра РАВС) следует, что значит,

Тогда получаем:

Заметим, что так как базисные векторы попарно перпендикулярны и длины их равны соответственно 2, 3 и 4, то

           (*

Заменяя выражением в последней системе уравнений и учитывая (*), получаем:

Тогда 

и

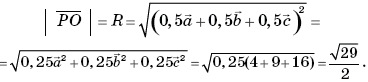
Значит, 

Ответ: 29π.

Задание №9.

В правильной треугольной призме ABCA₁B₁C₁ все ребра которой равны 1, найдите косинус угла между прямыми AD₁ и CE₁ , где D₁ и E₁ – соответственно середины ребер A₁C₁ и B₁C₁.

Решение: Введем систему координат, тогда :

1. Координаты точек задающих прямые, указанные в условии задачи

2. Найдем координаты векторов:

3. Найдем косинус угла между векторами

Ответ:0,7.

Задание №10.

В правильной четырехугольной пирамиде SABCD с вершиной S высота равна диагонали основания. Точка F лежит на середине ребра SA. Найдите квадрат тангенса между прямыми SD и BF.

Решение:

то введем прямоугольную систему координат с O(0;0), OC – ось x, OD – ось y, OS – ось z;

2)Пусть OC=a, то AC=2a, тогда SO=2a, то S(0;0;2); D(0;a;0);B(0;-a;0);

3)Рассмотрим - серединаAS, то если FF₁AO, то по теореме Фалеса

4)

5)

6)

Ответ: 10,25.