- •Приложение 1 Конспекты занятий Урок №1 «Числовая окружность»
- •Ход урока
- •1. Организационный момент.
- •2. Актуализация опорных знаний.
- •§ 2 (До макетов), стр. 8-12;
- •Урок №2 Игра «Умники и умницы. Тема «Числовая окружность»»
- •Ход урока
- •§ 2, Стр 8 – 18 разобрать пример № 7;
- •Урок №3 «Числовая окружность на координатной плоскости»
- •Ход урока
- •1. Организационный момент.
- •2. Актуализация опорных знаний.
- •Урок №4 «Синус и косинус». «Колесо истории».
- •Ход урока
- •1. Организационный момент.
- •2. Актуализация опорных знаний.
- •§ 4 Стр 26 - 30;
- •Урок № 5 «Синус и косинус».
- •Ход урока
- •§ 4 Стр 30 - 34;
- •Урок №6 «Тангенс и котангенс».
- •Ход урока
- •1. Организационный момент.
- •§ 5 Стр 34 - 37;
- •Урок №7 «Тригонометрические функции числового аргумента»
- •Ход урока
- •1. Организационный момент.
- •§ 6 Стр 37 - 39;
- •§ 7 Стр 40 - 43;
- •Урок №9 «Тригонометрические функции углового аргумента»
- •Ход урока
- •1. Организационный момент.
- •§ 7 Стр 40 - 43;
- •Урок №10 «Острова знаний».
- •Ход урока
- •1. Организационный момент.
- •§ 7 Стр 40 - 43;
§ 2, Стр 8 – 18 разобрать пример № 7;
№ 2, № 4, № 27.
Урок №3 «Числовая окружность на координатной плоскости»
Цель:
сформировать новые знания и отработать умения по теме «Числовая окружность на координатной плоскости»;
сформировать умения, способствующие развитию познавательной активности.
Задачи:
рассмотреть числовую окружность на координатной плоскости;
закрепить умение нахождения на числовой окружности точки с конкретным значением абсциссы и ординаты, а так же умение определять каким числам они соответствуют;
закрепить полученные знания на практике.
Тип урока: урок изучения нового материала.
Время: 45 минут.
Структура урока:
Организационный момент - (2 мин.);
Актуализация опорных знаний – (7 мин.);
Изучение нового материала - (18 мин.);
Закрепление изученного материала - (13 мин.);
Итог урока - (3 мин.);
Домашнее задание - (2 мин.).
Ход урока
1. Организационный момент.
-сообщение темы урока;
- постановка цели урока.
2. Актуализация опорных знаний.
Задачи:
проверить степень усвоения ранее изученного материала,
актуализировать знания учащихся, необходимые при изучении новой темы.
|
Деятельность учителя |
Деятельность ученика |
|
- Прежде чем перейти к изучению новой темы, проверим ваши знания по предыдущей теме. (Проверочная работа (слайд 3 – 5), проходит в виде игры «Кто хочет стать миллионером?»)
После выполнения заданий, учащиеся сдают листочки, а затем вместе с учителем проверяют правильные ответы. |
(Учащиеся выполняют задания)
|
Изучение нового материала.
Задачи:
сформулировать понятие числовая окружность.
|
Деятельность учителя |
Деятельность ученика |
|
-Расположим нашу числовую окружность в декартовой прямоугольной системе координат хОу, центр окружности совмещен с началом координат, а ее радиус принимается за масштабный отрезок, тогда любая точка окружности имеет декартовы координаты и круговые координаты.
- Например начальная точка А числовой окружности совмещена с точкой (1; 0) на оси х. При этом В = В (0;1), С = С (-1; 0), D = D (0; -1). Каждая точка числовой окружности имеет в системе хОу свои координаты, при чем для точек: 1 четверти – х > 0, у > 0; 2 четверти – х < 0, у > 0; 3 четверть – х < 0, у < 0; 4 четверть – х > 0, у < 0. (слайд 6).
- А теперь начертим координатную плоскость, которая проходит через центр окружности. Возьмем одну из тех точек, которые мы уже знаем. Рассмотрим ее координаты. Опустим перпендикуляры на ось Ох и Оу (слайд 7).
Р х2 + у2 = 1 , откуда
х
=
-
Итак т. М (
-
теперь я предлагаю вам вывести значение
координат для точки М1
(
-
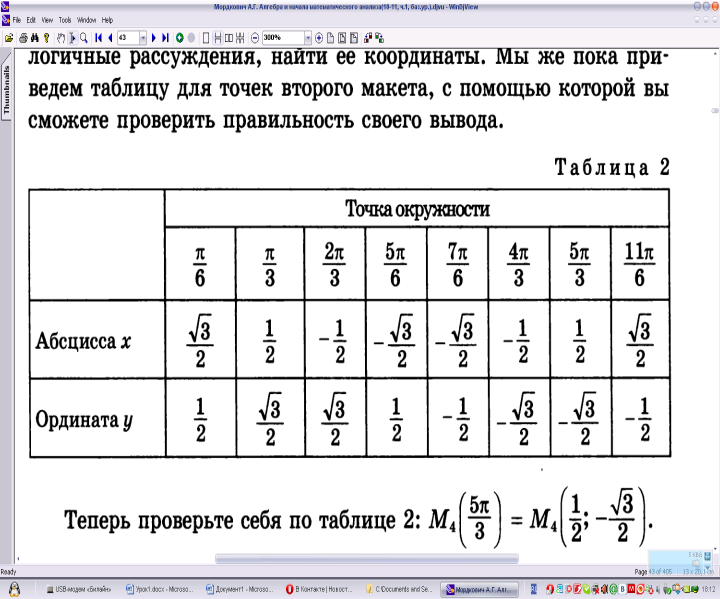
В качестве дополнительного домашнего
задания, я предлагаю вам вывести
значения координат для точек
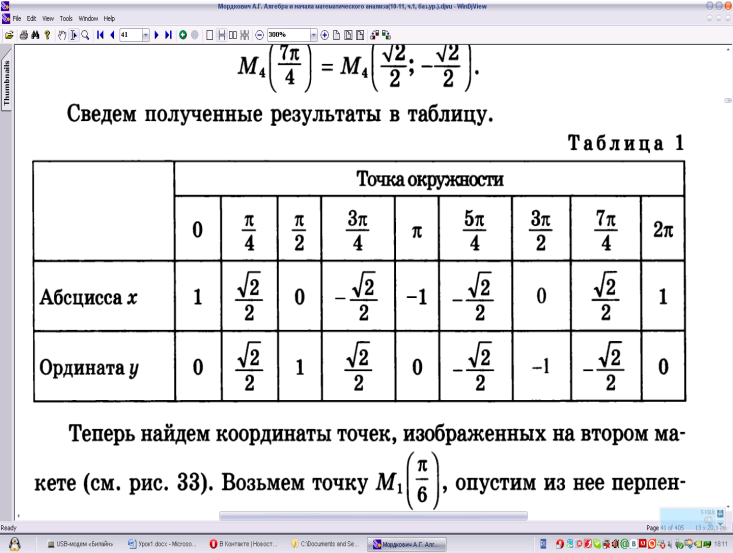
А сейчас просто отметим эти точки на окружности и запишем их координаты (слайд 8). Сведем полученные результаты в таблицу.
|
Учащиеся
приходят к выводу, что так как точка
М1
симметрична точки М, и точка М1
находится во второй четверти, то ее
координаты будут М1
( М1
( М3
(
|
Закрепление изученного материала.
Задачи:
сформировать умение решать примеры на применение нового
материала.
|
Деятельность учителя |
Деятельность ученика |
|
- Теперь для закрепления пройденного материала, открываем задачники, номера с 29 – 34. №29 – 32. Центр числовой окружности совпадает с началом координат на координатной плоскости хОу. Найдите декартовы координаты заданной точки: - Выходим, по одному человеку к доске и решаем по порядку по одному примеру.
№ 33 – 34 Найдите наименьшее положительное и наибольшее отрицательное числа, которым на числовой окружности соответствует точка с координатами.
- Следующее задание (слайд 9). Найти на числовой окружности точки с ординатой у = и записать, каким числам t они соответствуют. Решение.
Прямая у = пересекает числовую окружность
в точках М и Р. Точка М соответствует
числу
числу
вида часто говорят в таких случаях, две серии
значений:
Ответ:
t = - Теперь № 42 – 43 под буквами а) и б) На числовой окружности укажите точку М, координаты которой удовлетворяют данным условиям, и найдите все числа, которым соответствует эта точка.
№ 44 – 45 под буквой б) Найдите на числовой окружности точки с абсциссой или ординатой, удовлетворяющей заданному неравенству, и запишите (с помощью двойного неравенства), каким числам t они соответствуют.
|
№29 а)
М ( б)
М ( в)
М ( г)
М ( № 30 – 32 (Учащиеся решают аналогичным способом)
№ 33 а)
М ( б)
М (- в)
М ( г)
в) М (- № 34 (Учащиеся решают аналогичным способом)
№ 42 а)
б)
№ 43 (Учащиеся решают аналогичным способом)
б)
№ 45 (Учащиеся решают аналогичным способом)
|
Итог урока
Домашнее задание.
§ 3;
№ 35, № 37, № 48.

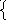 ассмотрим
треугольник ОМР. Так как дуга АМ
составляет половину дуги АВ, то угол
АОМ = 450
следовательно треугольник ОМР
прямоугольный равнобедренный, где ОР
= МР, то есть у точки М абсцисса и
ордината равны: х = у. Точка М удовлетворяет
уравнению числовой окружности х2
+ у2
= 1. Таким образом выходим на систему
х = у
ассмотрим
треугольник ОМР. Так как дуга АМ
составляет половину дуги АВ, то угол
АОМ = 450
следовательно треугольник ОМР
прямоугольный равнобедренный, где ОР
= МР, то есть у точки М абсцисса и
ордината равны: х = у. Точка М удовлетворяет
уравнению числовой окружности х2
+ у2
= 1. Таким образом выходим на систему
х = у