5.2. Построение графиков областей на плоскости, ограниченных заданными кривыми

Задача построения областей на плоскости возникает при нахождении площади плоской области с помощью определенного интеграла или при определении области интегрирования в двойном интеграле. Обычно эти области ограничены графиками функций одной переменной, поэтому построение таких областей в Maple можно осуществить с помощью обычных команд построения графиков.

Пример 5.2.Построить область, ограниченную кривыми.

Решение.Строим графики кривых в программе Maple (рисунок 5.2)

Классическое окно	Стандартное окно
> with(plots): > implicitplot([x=0,x=2,y=2^x,y=2*x-x^2],x=-1..3, y=-1..5,color=black,thickness=3);

Рисунок 5.2 – График функций

На построенном графике область не выделена. Чтобы выделить эту область цветом, определим функцию двух переменных, которая принимает значение 1 внутри области и 1 - вне этой области. Это можно сделать с помощью функции piecewise , которая определяет значения функции в зависимости от условий, которым должны удовлетворять переменные.

Классическое окно	Стандартное окно
> f1:=(x,y)->piecewise(x>=0 and x<=2 and y<=2^x and y>=2*x-x^2,1,-1);
Далее зададим выделение цветом той части области на плоскости, где построенная функция положительна. Определим это выделение в качестве графического объекта P1.
> P1:=implicitplot(f1(x,y)>=0,x=-1..3,y=-1..5, filledregions=true,coloring=[grey,white], numpoints=100000):
Графики кривых зададим как графический объект P2
> P2:=implicitplot([x=0,x=2,y=2^x,y=2*x-x^2],x=-1..3, y=-1..5,color=black,thickness=3):
Затем отобразим все графические объекты на одном графике с помощью функции display(рисунок 5.2)
> display(P1,P2,view=[-1..3,-1..5]);

Рисунок 5.3 – График функций , выделенной цветом

В результате получаем плоскую область выделенную цветом.

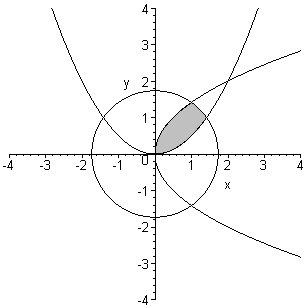
Пример 5.3.Выделить цветом область на плоскости, ограниченную линиями.

Решение.Решаем пример по аналогии с предыдущим

Классическое окно	Стандартное окно
загружаем пакет графических функций; > with(plots):
> f1:=(x,y)->piecewise(x^2<=2*y and y^2<=2*x and x^2+y^2<=3,1,-1):
- определяем функцию, принимающую для закрашенной области значение 1, а в остальных точках -1;
> P1:=implicitplot(f1(x,y)>=0,x=-1..3,y=-1..5, filledregions=true,coloring=[grey,white], numpoints=400000,view=[-4..4,-4..4]):
- создаем графический объект закрашенной области;
> P2:=implicitplot([x^2=2*y,y^2=2*x,x^2+y^2=3],x=- 4..4,y=-4..4,numpoints=100000,color=black):
– создаем графический объект граничных линий;
> display(P1,P2);
– отображаем все на одном графике (рисунок 5.3)

Рисунок 5.4 – График закрашенной области

5.3. Построение областей в пространстве, ограниченных заданными поверхностями

Области или тела в пространстве, ограниченные поверхностями, можно строить, задавая графики этих поверхностей.

Пример 5.5.Построить область, ограниченную параболоидоми плоскостью, y =4 .

Решение.Строим поверхности с помощью функции implicitplot3d :

Классическое окно	Стандартное окно
загружаем пакет графических функций; > with(plots):
> implicitplot3d([x^2+z^2=y,y=4],x=-6..6,y=-6..6, z=-6..6,axes=normal,view=[-6..6,-6..6,-6..6], numpoints=10000);

Рисунок 5.5 – Графики поверхностей ограниченных параболоидом и плоскостью, y =4 .

Такие построения не всегда являются наглядными, так как часто нам нужны не сами поверхности, а те контуры поверхностей, которые ограничивают область в пространстве. Построения таких контуров можно добиться, если строить линии пересечения поверхностей, ограничивающих тело, с координатными плоскостями, а также другими поверхностями, ограничивающими тело. Это можно сделать, задавая параметрически эти линии пересечения. Построим контуры, ограничивающие фигуру в примере 5.5, с помощью функции spacecurve, задавая параметрически линии пересечения поверхности с координатными плоскостями x =0 , z =0 и с плоскостьюy =4.

Классическое окно	Стандартное окно
> P1:=spacecurve([0,t^2,t],t=-2..2,color=black, thickness=2,axes=normal):
– линия пересечения поверхности с плоскостью x =0;
> P2:=spacecurve([2*cos(t),4,2*sin(t)],t=0..2*Pi, color=black,thickness=2,axes=normal):
–линия пересечения поверхности с плоскостью y = 4;
> P3:=spacecurve([t,t^2,0],t=-2..2,color=black, thickness=2,axes=normal):
–линия пересечения поверхности с плоскостью z =0 ;
> display(P1,P2,P3,view=[-4..4,-6..6,-4..4], orientation=[15,75,1],labels=[x,y,z]);

Рисунок 5.6 – Изображение фигуры ограничивающими контурами