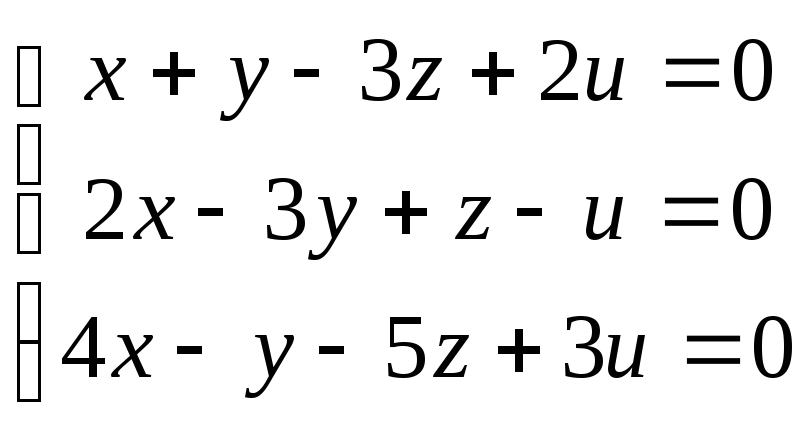Контрольная по линейной алгебре
.docGief.ru Кафедра информационных технологий
![]()
|
ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ (Преподаватель: к.м.н., доцент Холявин И.И..) |
![]() Контрольная
работа
Контрольная
работа
Последняя цифра номера задания студента совпадает с последней цифрой номера его зачетки.
1-10. Даны координаты вершин треугольника АВС: А(x1;y1), В(x2;y2), С(x3;y3). Составить: а) уравнение стороны АВ; б) уравнение высоты СН; в) уравнение медианы АМ.
1. А(2;3), В(4;-1), С(-2;-3). 2. А(-2;-3), В(1;6), С(6;1).
3. А(-4;2), В(-6;6), С(6;2). 4. А(4;-3), В(7;3), С(1;10).
5. А(4;-4), В(8;2), С(3;8). 6. А(-3;-3), В(5;-7), С(7;7).
7. А(1;-6), В(3;4), С(-3;3). 8. А(-4;2), В(8;-6), С(2;6).
9. А(-5;2), В(0;-4), С(5;7). 10. А(4;-4), В(6;2), С(-1;8).
11-20. С помощью выделения полных квадратов получить каноническое уравнение линии, определить её тип, параметры и расположение на плоскости (сделать рисунок).
11. x2+4y2-6x+8y=3. 12. 5x2+30x+4y2+8y=1.
13. 9x2+16y2-18x +128y=-121. 14. x2+9y2-8x+36y=-4.
15. 9x2+25y2-36x+50y=164. 16. 4x2+25y2-24x+50y=39.
17. x2+4y2-8y=0. 18. 9x2+16y2-32y=128.
19. 9x2+16y2-36x-96y=-36. 20. 9x2+36x+4y2-8y=-31.
21-30. С помощью выделения полных квадратов получить каноническое уравнение линии, определить её тип, параметры и расположение на плоскости (сделать рисунок).
21. x2-9y2-2x-18y=17. 22. 4x2+8x-9y2+18y=41.
23. x2-4y2+4x +8y=16. 24. x2-y2-4x-6y=9.
25. x2-6y2-12x+36y=48. 26. x2-4y2+8y=8.
27. x2-4y2+6x-16y=23. 28. x2-25y2+8x-50y=34.
29. 4x2-9y2-8x-36y=68. 30. 4x2-9y2-8x=32.
31-40. С помощью выделения полных квадратов получить каноническое уравнение линии, определить её тип, параметры и расположение на плоскости (сделать рисунок).
31. x2+2x-y=-3. 32. x2-4x-y=-5.
33. y2-4x +8y=-24. 34. y2-12x-2y=-25.
35. y2-4x+10y=-29. 36. x2+2х+4y=3.
37. x2+2x-4y=-5. 38. 4x-y2-4y=-4.
39. y2-12x-2y=-25. 40. x2-2x-2y=5.
41-50.
Даны координаты трёх точек А,
В, С
в пространстве. Найти: а) координаты
вектора с=![]() +
+![]() ;
б) ориентацию вектора с
в пространстве;
в)
угол между
векторами
;
б) ориентацию вектора с
в пространстве;
в)
угол между
векторами
![]() и
и
![]() .
.
41. А(-1,1,6), В(-1,6,1), С(0,4,-1). 42. А(1,7,3), В(6,9,1), С(8,5,8).
43. А(1,9,9), В(5,8,3), С(6,4,8). 44. А(4,9,3), В(7,6,1), С(3,6,7).
45. А(5,7,8), В(-3,7,1), С(6,9,2). 46. А(4,6,3), В(4,1,5), С(3,9,8).
47. А(3,5,10), В(3,8,4), С(5,8,2). 48. А(4,2,0), В(4,6,6), С(1,2,6).
49. А(4,5,7), В(9,4,4), С(7,9,6). 50. А(2,4,7), В(5,4,7), С(7,3,0).
51-60.
Векторы
![]() и
и
![]() -
единичные, угол между которыми равен
600.
Найти скалярное произведение
-
единичные, угол между которыми равен
600.
Найти скалярное произведение
![]()
![]() .
.
51.
![]() =5
=5![]() +6
+6![]() ;
;
![]() =2
=2![]() -
-![]() 52.
52.
![]() =5
=5![]() +3
+3![]() ;
;
![]() =-2
=-2![]() +
+![]()
53.
![]() =
=![]() +
+![]() ;
;
![]() =2
=2![]() -4
-4![]() 54.
54.
![]() =2
=2![]() +3
+3![]() ;
;
![]() =7
=7![]() -5
-5![]()
55.
![]() =3
=3![]() +5
+5![]() ;
;
![]() =6
=6![]() -
-![]() 56.
56.
![]() =
=![]() +3
+3![]() ;
;
![]() =2
=2![]() -2
-2![]()
57.
![]() =3
=3![]() +
+![]() ;
;
![]() =2
=2![]() -2
-2![]() 58.
58.
![]() =
=![]() -
-![]() ;
;
![]() =
=![]() +2
+2![]()
59.
![]() =
=![]() +3
+3![]() ;
;
![]() =2
=2![]() -8
-8![]() 60.
60.
![]() =2
=2![]() +5
+5![]() ;
;
![]() =2
=2![]() -3
-3![]()
61-70. Заданы прямая l1 и две точки А и В в пространстве. Составить: а) уравнение плоскости Р, проходящей через т.А перпендикулярно прямой l1; б) уравнение прямой l2, проходящей через т. В параллельно прямой l1; в) найти расстояние от т. В до плоскости Р.
61.
l1:
![]() ,
А(2,1,0), В(2,2,1)
,
А(2,1,0), В(2,2,1)
62.
l1:
![]() ,
А(2,1,0), В(2,2,1)
,
А(2,1,0), В(2,2,1)
63.
l1:
![]() ,
А(-2,4,2), В(1,1,3)
,
А(-2,4,2), В(1,1,3)
64.
l1:
![]() ,
А(6,2,0), В(4,1,6)
,
А(6,2,0), В(4,1,6)
65.
l1:
![]() ,
А(2,3,0), В(2,5,1)
,
А(2,3,0), В(2,5,1)
66.
l1:
![]() ,
А(4,3,1), В(0,1,-4)
,
А(4,3,1), В(0,1,-4)
67.
l1:
![]() ,
А(3,0,2), В(2,4,4)
,
А(3,0,2), В(2,4,4)
68.
l1:
![]() ,
А(5,0,4), В(2,2,2)
,
А(5,0,4), В(2,2,2)
69.
l1:
![]() ,
А(2,4,-1), В(3,1,4)
,
А(2,4,-1), В(3,1,4)
70.
l1:
![]() ,
А(4,2,-1), В(2,3,5)
,
А(4,2,-1), В(2,3,5)
71-80. Решить систему линейных уравнений двумя способами: а) методом Крамера; б) средствами матричного исчисления.
71.
![]()
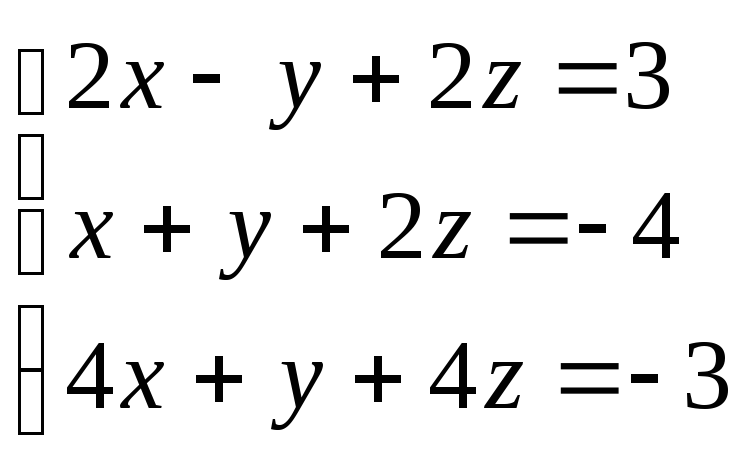 72.
72.

73.
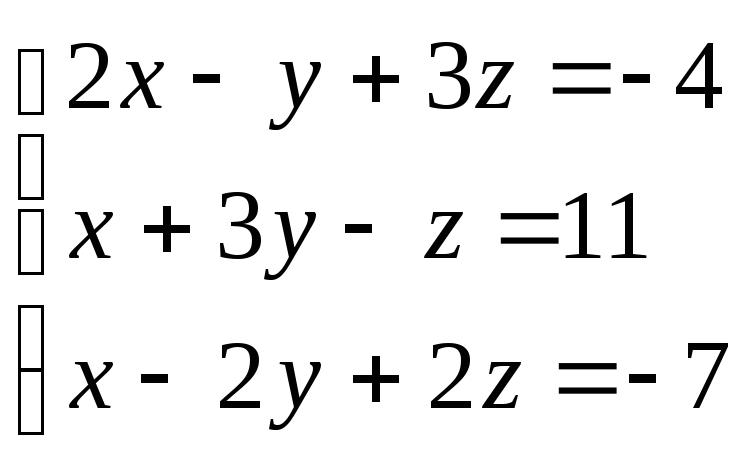 74.
74.
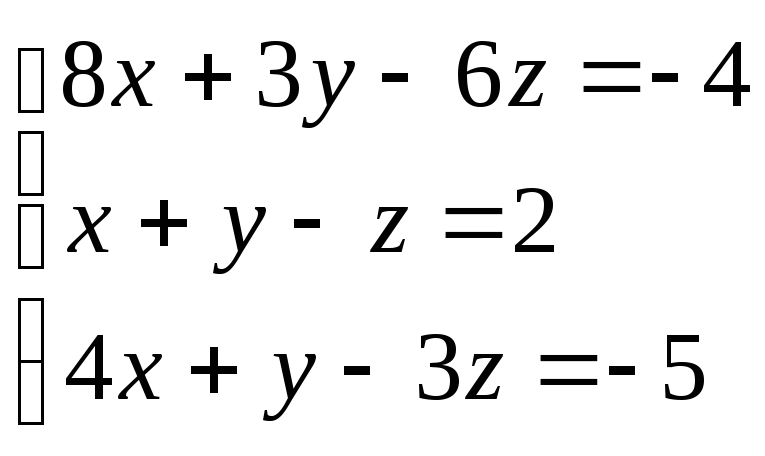
75.
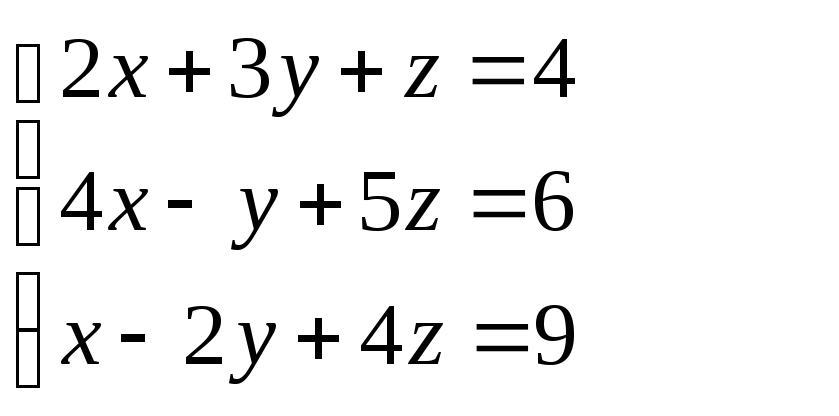 76.
76.
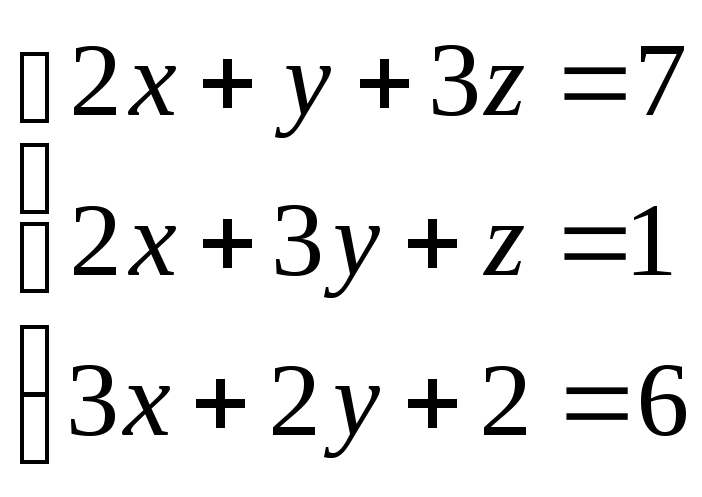
77.
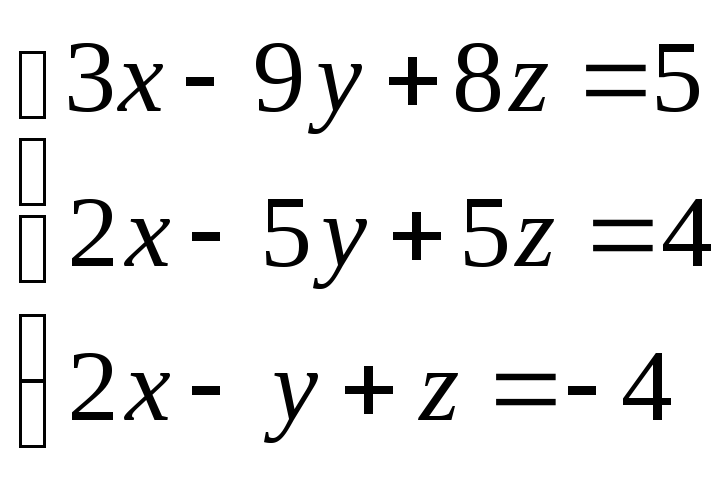 78.
78.
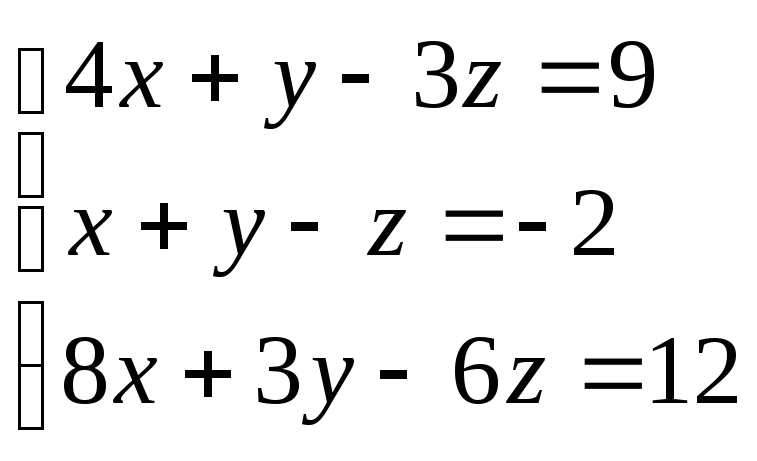
79.
 80.
80.

81-90. Найти решение системы методом Гаусса. Выполнить проверку для какого-либо частного решения.
81.
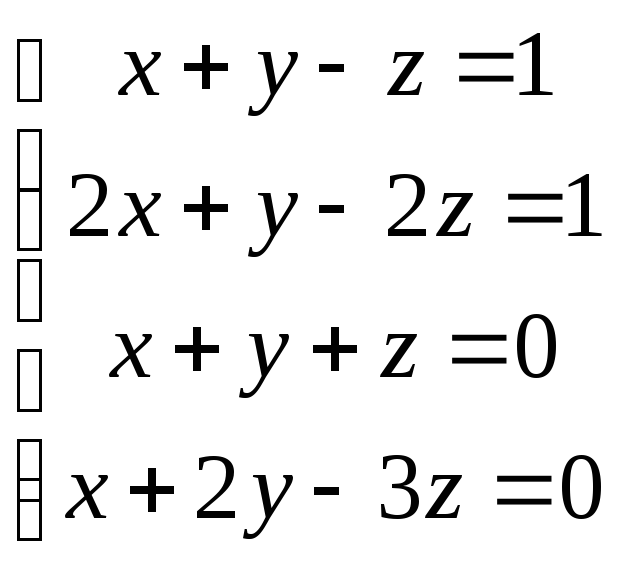 86.
86.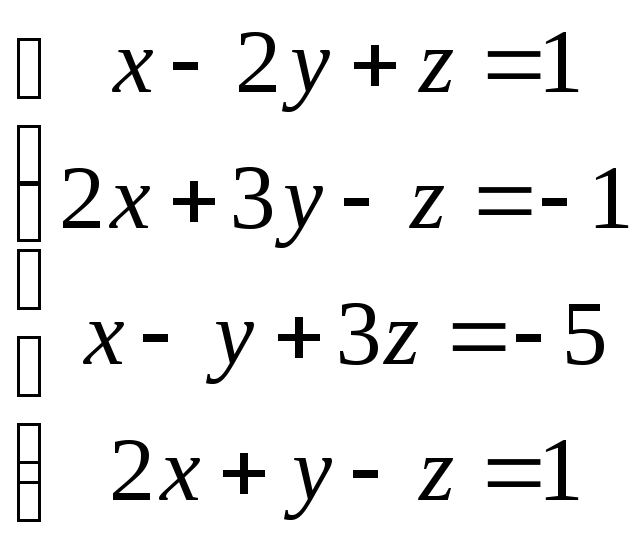
82.
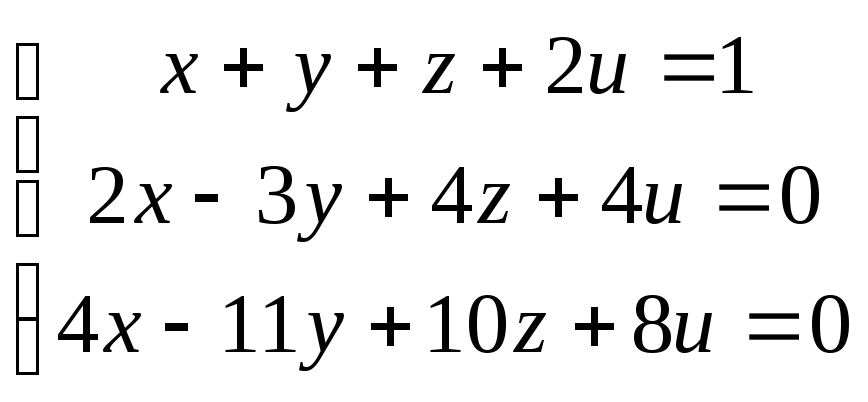 87.
87.
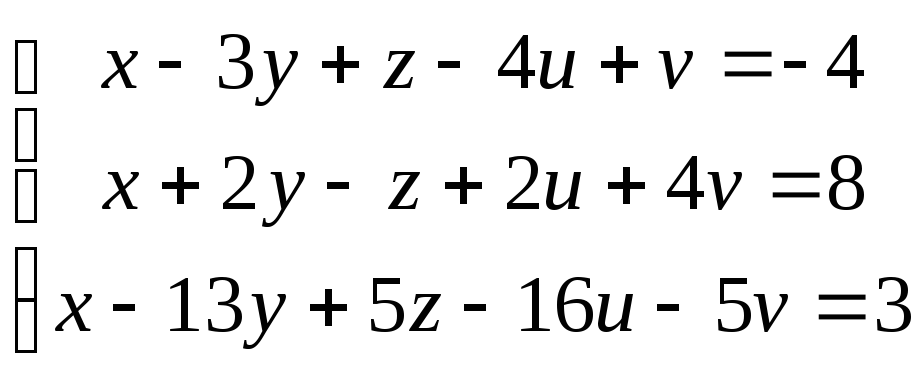
83.
 88.
88.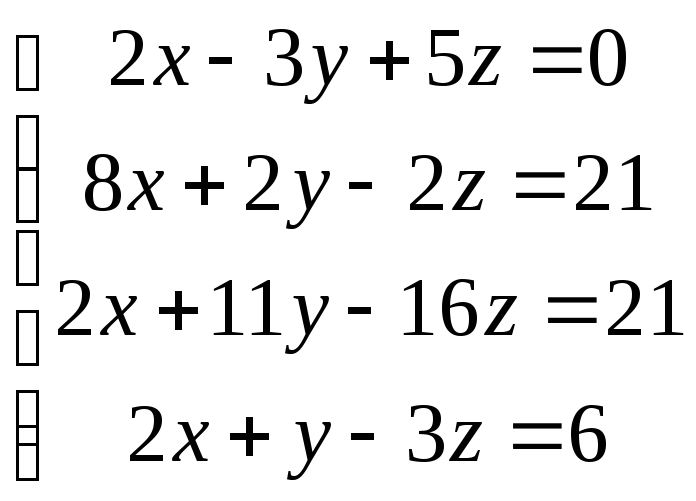
84.
 89.
89.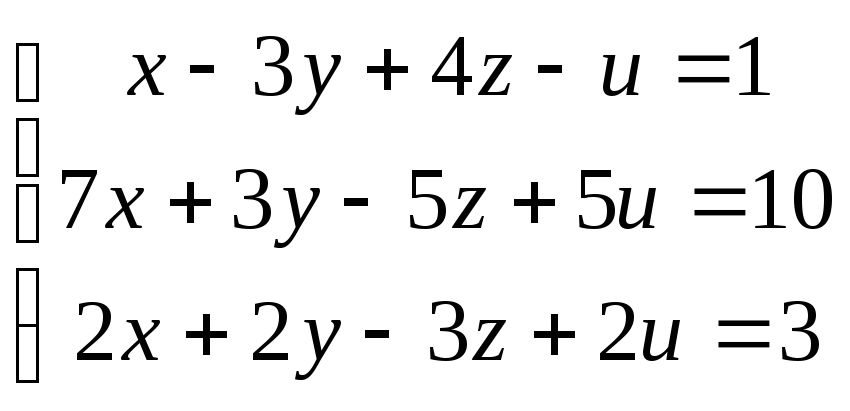
85.
 90.
90.
91-100. Найти общее решение и одно из базисных решений однородной системы уравнений.
91.
 92.
92.
 93.
93.
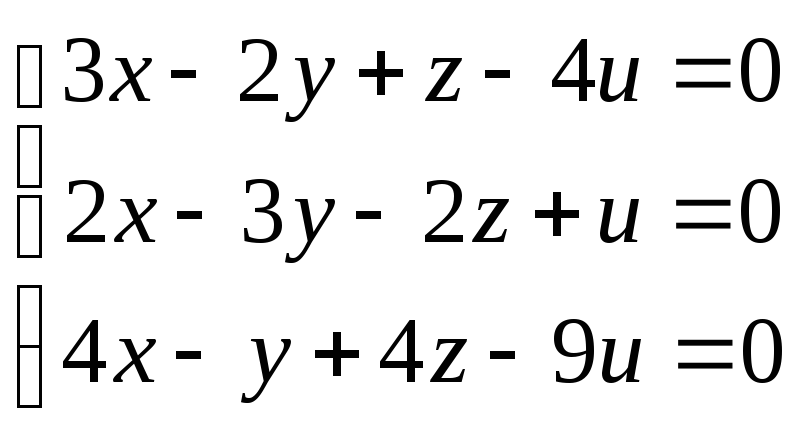
94.
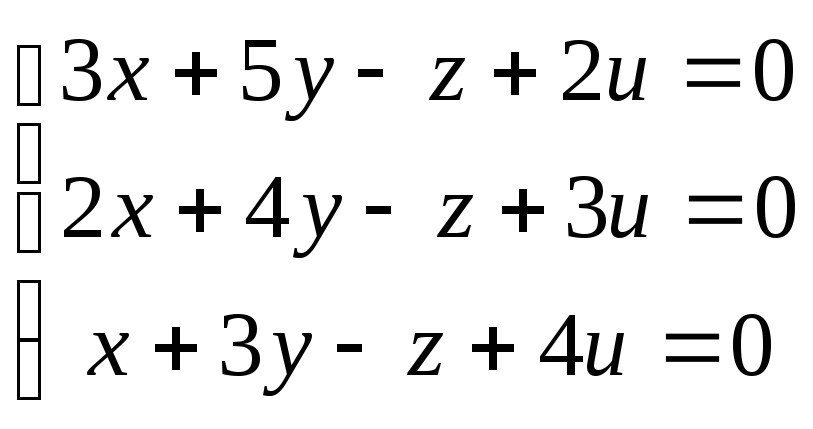 95.
95.
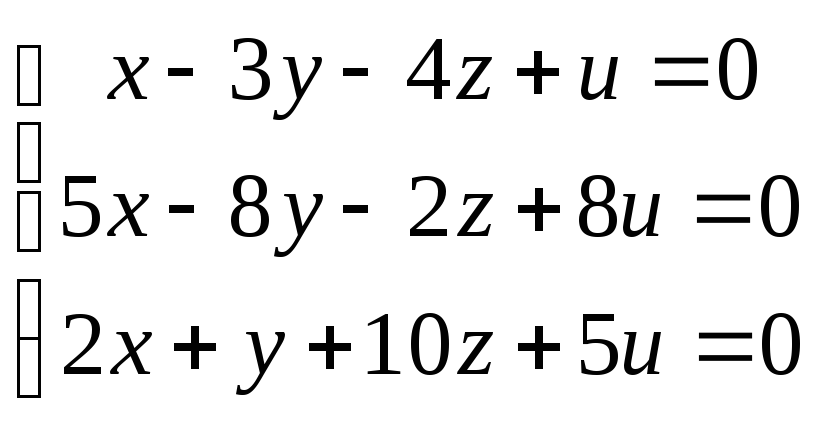 96.
96.

97.
 98.
98.
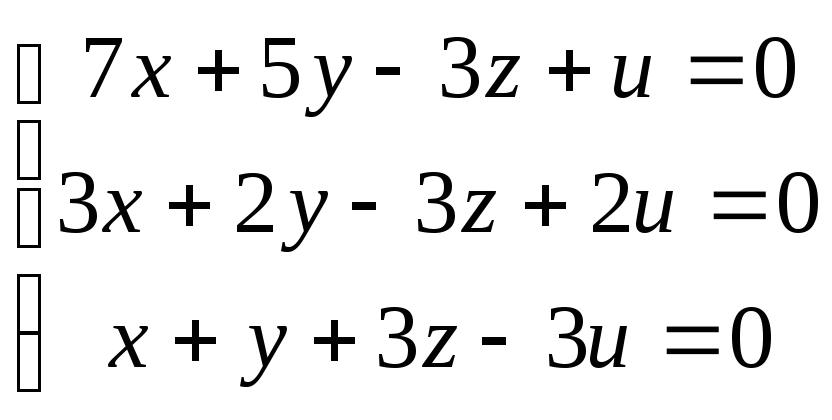 99.
99.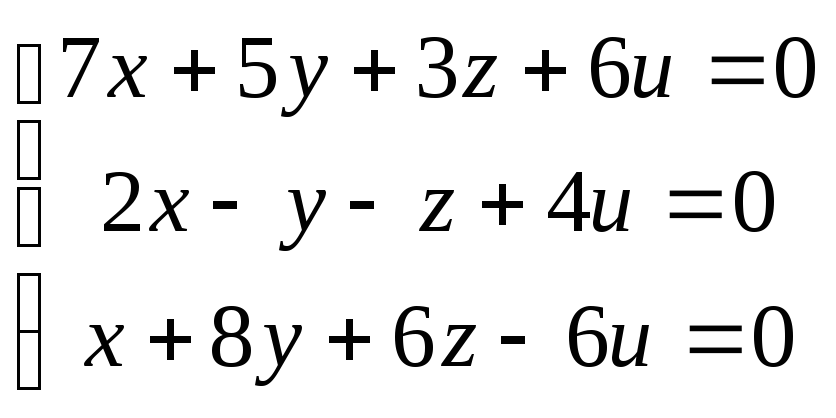
100.