сессия - 2 / СТтЗОБЗ / Лекция по ПЛ

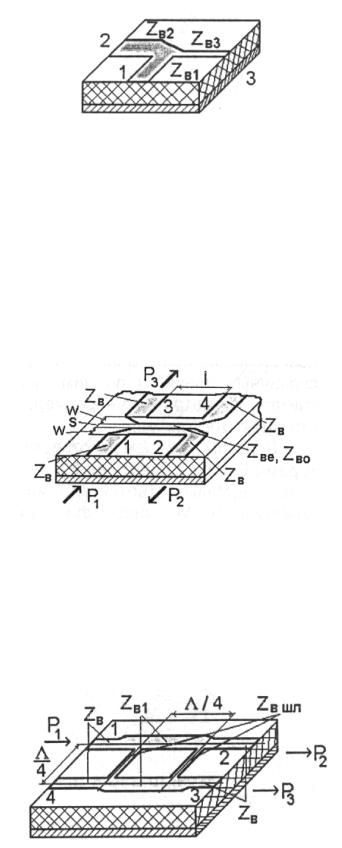
Рис. 3.3. Микрополосковый тройник

3.3. Направленные ответвители

Направленным ответвителем называют устройство, которое предназначено для деления мощности из одного плеча в несколько (обычно два) других плеч. На рис.3.4 показана конструкция ответвителя, состоящая из двух рядом расположенных полосок. Входная мощность поступает в плечо 1 и передаётся в плечо 2. При распространении энергии по полоскам в связанной компланарной линии возбуждается волна, направленная в противоположном направлении, в плечо 3. В плечо 4 энергия не поступает.

Рис. 3.4. Направленный ответвитель

Можно показать, что сдвиг фаз сигналов в каналах 2 и 3 составляет π/2, поэтому такие ответвители называют квадратурными.

Часто используется шлейфный направленный ответвитель, имеющий простую конструкцию, показанную на рис.3.5.

Рис.3.5. Шлейфный направленный ответвитель

Длина шлейфов между полосками и длина полосок составляет l=λ/4. Энергия поступает в плечо 1. В двух местах соединений часть энергии ответвляется во вторую полоску. При этом разность хода для волн, идущих в плечо 4 через оба ответвления, будет λ/2, волны будут противофазны и компенсировать друг друга. Волны, идущие в плечо 3,

будут синфазны. В результате на выходе 4 волны не будет, на выходах 2 и 3 будут волны, отличающиеся по фазе на π/2. Равенство амплитуд в плечах 2 и 3 обеспечивают выбором волновых сопротивлений полосок.

При делении мощности на несколько частей могут применяться более сложные схемы. Например, на рис.3.6 показано устройство, осуществляющее деление мощности в три плеча.

Рис.3.6. Делитель мощности на три части

При подаче энергии в плечо 1 первой линии в первом согласованном соединении ответвляется часть мощности в плечо 2. Другое плечо второй компланарной линии нагружено на поглощающую согласованную нагрузку. Во втором соединении мощность аналогично ответвляется в плечо 3. Оставшаяся часть энергии в первой линии проходит в плечо 4. Подбирая волновые сопротивления линий, добиваются требуемого деления мощностей.

3.4. Мостовые схемы на полосковых линиях

Мостовыми схемами называют устройства, обладающие свойством: при возбуждении одного из четырёх плеч энергия в одно из выходных плеч не поступает, а делится поровну между двумя другими плечами. Это частный случай направленного ответвителя для коэффициента деления ½. В качестве мостом могут применяться шлейфные направленные ответвители при соответствующем выборе их параметров.

В полосковых линиях часто применяют кольцевые мосты (рис.3.7).

Рис.3.7. Полосковый кольцевой мост

Принцип работы полоскового кольцевого моста полностью аналогичен работе волноводного кольцевого моста. Длина отрезка линии между плечами 1 и 2, 1 и 4, 3 и 4 равны λ/4. Поэтому фаза волны, прошедшей по линии от плеча к соседнему плечу, изменяется на π/2. Если подать энергию в плечо 1, то волны, пришедшие к плечам 2 и 4 по часовой стрелке и против часовой стрелки, будут синфазны. В результате в этих плечах

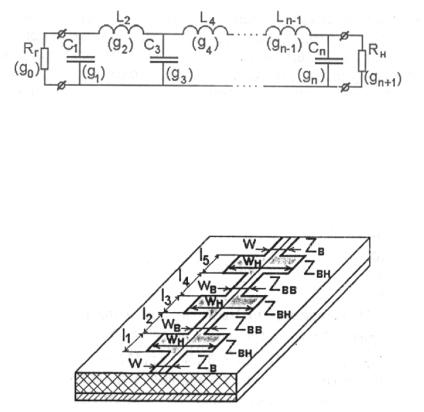
возбуждаются волны. А к плечу 3 придут противофазные волны (одна волна против часовой стрелки пройдет путь 2λ/4, другая по часовой стрелке пройдет 4λ/4, разность хода 2λ/4 и соответствующая разность фаз будет π) и в этом плече волна не возбуждается. В плечах 2 и 4 будут синфазные сигналы т.к. путь, пройденный волной из плеча 1 до плеч 2 и 4, одинаков.

Аналогично, при подаче энергии в плечо 3 энергия пойдет в плечи 2 и 4, но там будут уже противофазные сигналы, т.к. путь волны из плеча 3 в плечи 2 и 4 отличается на 2λ/4, что соответствует разности фаз π.

Мостовые схемы широко применяются при создании балансных смесителей, когда в одном плече необходимо получить сумму сигналов приёмника и гетеродина, а в другом плече – разность этих сигналов, что позднее позволит компенсировать значительные шумы гетеродина.

3.5.Частотные фильтры

Спомощью полосковых линий могут быть реализованы различные фильтры – низких частот, высоких частот, полосовые фильтры пропускания и заграждения.

Рассмотрим пример создания фильтра низких частот. Его эквивалентная схема показана на рис. 3.8.

Рис.3.8. Эквивалентная схема фильтра низких частот

Таким образом, полосковая линия должна включать последовательные индуктивности, показанные на рис.2.1 и параллельные ёмкости, показанные на рис.2.6. В результате получаем структуру, показанную на рис.3.9.

Рис.3.9. Полосковый фильтр низких частот.

Рассмотрим построение полосового фильтра, пропускающего частоты в узкой полосе и не пропускающего низкие и высокие частоты. Эквивалентная схема такого фильтра показана на рис.3.10.

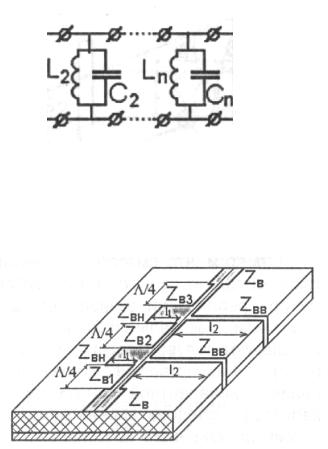
Рис.3.10. Эквивалентная схема полосового фильтра

Для его реализации нужно параллельно включать параллельные ёмкости (рис.2.6) и параллельные индуктивности (рис.2.2). Такая конструкция показана на рис.3.11.

Рис.3.11. Полосовой полосковый фильтр

Показанные на рисунке широкие полоски – это ёмкости, выполненные по технологии рис.2.6, а узкие полоски – индуктивности, соединённые с подложкой.

Для того, чтобы избежать просверливания подложки диэлектрика, полоску индуктивности могут увеличивать на λ/4, и противоположный конец удлинённой полоски будет работать в режиме холостого хода (как показано на рис.2.2в).

Здесь используется известное свойство линии передачи: входное сопротивление отрезка линии передачи длиной l может быть рассчитано по формуле

3.6. Фазовращатели

Фазовращатель – устройство, предназначенное для изменения фазы проходящей волны. В современной технике находят широкое применение электрически управляемые фазовращатели на p-i-n диодах. Особенность этих диодов заключается в их структуре, где

есть слой i, обеднённый носителями заряда и, соответственно, имеющий высокое сопротивление. Диод включается между полосковой линией и нижним проводником – землей. Если на диод подано обратное управляющее напряжение, его сопротивление большое и волна проходит через диод. Если на диод подано прямое напряжение, его сопротивление становится очень малым, линия работает в режиме, близком к короткому замыканию. От этого места полосковой линии волна отражается, в результате изменяется длина пути, пройденного волной и, соответственно, изменяется её фаза.

4. Пример расчёта волнового сопротивления полосковой линии

Задача. Сравнение волнового сопротивления коаксиальной линии и симметричной полосковой линии с аналогичными габаритами.

Дано:

Рассчитать и сравнить волновое сопротивление коаксиальной и симметричной

линии.

Решение.

1. Расчет характеристического сопротивления диэлектрика, заполняющего линии

При расчёте использованы константы ε0 = 361π 10−9Ф/ м, µ0 = 4π10−7 Гн/ м. 2. Расчет волнового сопротивления коаксиальной линии.

1-й вариант ZвКл =35,8 Ом,

2-й вариант ZвКл =27,7 Ом.

3. Расчет волнового сопротивления симметричной линии.

Результаты расчёта: d = 0,5788, Zв = 37,8 м.

A = π1 [2a1 ln(a1 +1)−(a1 −1)ln(a12 −1)].

Результаты расчёта: a1 = 1,053, A = 0,519, Zв = 30,0 Ом.

Вывод.

1.Если для расчёта волнового сопротивления симметричной полосковой линии использовать формулы для волнового сопротивления коаксиальной линии с такими же габаритными размерами, получится заметная погрешность. Причина этого – другая структура поля в полосковой линии.

2.При уменьшении толщины полосковой линии волновое сопротивление уменьшается.

Литература

1. Пименов Ю.В., Вольман В.И., Муравцов А.Д. Техническая электродинамика. Учеб. пособие для вузов. - М.: Радио и связь, 2000. – 536 с.