Фальсификация ЦП Эль-Гамаля в специальном случае… 137
Непосредственно вычислить |
L |
(a)mod pr−1 |
трудно, т.к. |
величина |
||||||
|
|
|
m |
|
|
|
|
|
||
aϕ(m ) −1 быстро возрастает с ростом m = pr . |
|
|
|
|
||||||
|
|
aϕ(m) −1 |
|
|
− |
где h < pr−1 . |
|
|||
Очевидно, однако, |
что |
|
|
|
|
= h + kpr 1 , |
Поэтому |
|||
|
pr |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
aϕ(m) −1 = hpr + kp2r−1 , причем hpr < p2r−1 . |
|
|
|
|
||||||
Следовательно, |
наименьший |
|
неотрицательный |
вычет |
||||||
H = aϕ(m) −1(mod p2r−1 ) |
совпадает с числом |
hpr . |
Это позволяет проводить |
|||||||
вычисления по mod p2r−1 |
и получать h в виде |
H |
. |
|
|
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
pr |
|
|
|
10.4. Фальсификация подписи Эль-Гамаля в специальном случае выбора первообразного элемента и характеристики поля
В качестве предварительного замечания рассмотрим вариант алгоритма Сильвера-Поллига-Хэллмана в ситуации, когда Fq =GF(p), где число p −1
не является гладким, но для некоторого делителя w числа p −1 |
гладким |
|||||||||||
является число u = (p −1) w . |
|
|
|
|
|
|
|
|
||||
Пусть |
g |
- первообразный |
элемент поля |
GF(p). Рассмотрим задачу |
||||||||
определения z из сравнения g wz ≡ yw (mod p). Обозначим gw =b . |
|
|||||||||||
Поскольку |
существует |
m: |
y = gm (p), |
то |
yw = gmw = bm (p). |
Поэтому |
||||||
исходная |
задача |
сводится |
к |
~ |
≡b |
z |
≡b |
m |
(p), |
которая |
является |
|
задаче y |
|
|
||||||||||
разрешимой. |
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что порядок элемента b равен u . Следовательно, наша задача |
||||||||||||
является |
задачей |
дискретного |
логарифмирования |
в |
мультипликативной |
|||||||
138 Глава 10. АЛГОРИТМ СИЛЬВЕРА - ПОЛЛИГА - ХЭЛЛМАНА
подгруппе поля GF(p), элементы которой выражаются в виде степеней элемента b.
По условию, порядок группы u является гладким числом. Это позволяет создать таблицу R для простых делителей числа u и найти z с помощью алгоритма Сильвера-Поллига-Хэллмана.
Таким образом, если u = (p −1)
w - гладкое число, то определение z из сравнения g wz ≡ yw (mod p) вычислительно реализуемо.
Как следствие докажем следующий факт.
Теорема [41]. Пусть дана схема цифровой подписи Эль-Гамаля с параметрами p , g , x , y ≡ g x (mod p) и p −1 = uw, где u - гладкое число.
Пусть, кроме g , задан примитивный элемент поля β вида β = cw и известно число t , такое, что βt = g(mod p).
Тогда для любого значения хэш-функции от сообщения h можно
построить корректную подпись |
(r,s) без знания секретного ключа x. |
|
||
Действительно, найдем z : |
yw ≡ gwz (mod p). Для заданного значения h |
|||
предложим подпись (r,s), где r = β , |
s =t(h −cwz) mod(p −1). Подставим |
|||
данные в проверочное соотношение |
для подписи, |
которое имеет |
вид |
|
gh = yr rs (mod p). |
|
|
|
|
Имеем: yr rs = yβ βs = ycwβt(h−cwz )(mod p). Заменяя |
yw на g wz , а βt |
на |
||
g , получим: gcwz gh−cwz = gh (p), т.е. подпись корректна.
Данное следствие позволяет сделать вывод о существовании частных случаев, когда подпись Эль-Гамаля может быть фальсифицирована.
Фальсификация ЦП Эль-Гамаля в специальном случае… 139
10.4.1. Слабые параметры в подписи Эль-Гамаля
Пусть p = 4k +1. Допустим, что параметры схемы подписи можно выбрать так, чтобы примитивный элемент g совпадал с гладким числом u :
g =u =(p −1)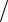
w.
В обозначениях предыдущего следствия, положим: β = (p −1)
g = w , t = (p −3)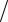
2. Иными словами, p −1 = gβ , u = g , w = β , c =1.
При таком выборе, β = −g−1 mod p . Элемент g−1 - первообразный, т.к.
при ord p g−1 = m < p −1, получим g−m+p−1 =1mod p , что неверно. Следовательно,
если n = ord p β < p −1, то n - нечетное число, делящее p −1.
|
Однако, n не делит p −1, т.к. |
β(p−1) 2 ≡ (− g−1 )2k = g−(p−1) 2 = −1mod p . |
|||||||||||
Следовательно, |
элемент |
β |
первообразный. |
Кроме |
того, |
||||||||
βt = β(p−1) 2β−1 ≡ −β−1 ≡ g mod p . |
|
|
|
|
|
|
|
||||||
|
Таким образом, для схемы цифровой подписи с указанными параметрами |
||||||||||||
подпись может быть подделана. Покажем, что такие схемы существуют. |
|
||||||||||||
|
Пусть теперь p = 4k +1, где k – простое и |
p ≥ 29 . Тогда можно выбрать |
|||||||||||
g = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительно, |
2(p−1) k ≠1(p). |
Далее, |
по |
критерию |
Эйлера, |
|||||||
|
(p−1) 2 |
|
2 |
|
|
|
2 |
|
(p2 −1)8 |
|
|
|
|
2 |
|
= |
|
mod p |
|
|
|
|
= (−1) |
mod p |
. Показатель в |
||
|
|
|
|
|
|||||||||
|
|
|
|
|
. Символ Лежандра |
p |
|
|
|
||||
|
|
|
p |
|
|
|
|
|
|
|
|
||
правой части нечетен: (p2 −1)8 = 2k2 + k , т.е. 2(p−1) 2 = −1mod p . |
|
||||||||||||
|
Таким образом, слабую подпись Эль-Гамаля можно получить, используя, |
||||||||||||
например, следующие параметры: |
p = 4k +1, где k – большое простое число, |
||||||||||||
140 Глава 10. |
АЛГОРИТМ СИЛЬВЕРА - ПОЛЛИГА - ХЭЛЛМАНА |
|
|
||
g = 2 , |
p −1 = gβ , |
u = g , |
w = β , |
c =1, |
t = (p −3) 2, |
(r,s)=(β, t(h − wz)).
Здесь z удовлетворяет сравнению g wz ≡ yw (mod p), где y - открытый ключ цифровой подписи, а u используется для определения z .