
- •Содержание
- •Введение
- •1.1. Общая система секретной связи (по К. Шеннону)
- •1.1.1. Основные криптографические термины
- •1.1.2. Модель системы секретной связи К.Шеннона
- •1.2. Подходы к оценке надежности реальных криптосистем
- •1.2.2. Метод сведения к общей алгоритмической проблеме
- •Глава 2. ОБЩИЕ АЛГОРИТМИЧЕСКИЕ ПРОБЛЕМЫ АНАЛИЗА ОСНОВНЫХ ТИПОВ ШИФРОВ
- •2.1. Элементарные шифры
- •2.2. Основные типы шифров
- •2.2.1 Потоковые шифры. Последовательность выбора шифрпреобразований
- •2.2.2. Качество гаммы
- •2.2.3. Периодичность гаммы
- •2.2.4. Блочные шифры
- •2.2.5. Алгоритмические проблемы, связанные со стойкостью основных типов шифров
- •Глава 3. ТЕСТИРОВАНИЕ УЗЛОВ КРИПТОСХЕМ КАК МЕТОД КОМПРОМЕТАЦИИ ШИФРОВ
- •3.1. Компрометация шифров
- •3.2. Задача тестирования линейной рекуррентной составляющей криптоузла
- •3.3. Задача восстановления параметров искаженной линейной рекурренты
- •3.3.1. Представление элементов рекурренты через элементы начального заполнения
- •3.3.2. Производные соотношения
- •3.3.4. Качественная характеристика задачи восстановления параметров линейной искаженной рекурренты
- •Глава 4. КРИПТОГРАФИЧЕСКИЕ СВОЙСТВА БУЛЕВЫХ ФУНКЦИЙ
- •4.1. Нелинейность булевой функции
- •4.2. Критерии распространения и корреляционная иммунность
- •4.3. Устойчивые булевы отображения
- •Глава 5. ОСОБЕННОСТИ ПРИМЕНЕНИЯ АЛГОРИТМА ГОСТ 28147-89
- •5.1. Криптоэквивалентная схема алгоритма ГОСТ 28147-89
- •5.2. Влияние блока подстановки на последовательности выходов итераций
- •5.2.1 Расшифрование в режиме простой замены
- •5.2.2. Возможность ослабления шифра за счет структуры сеансового ключа
- •5.3. Замечания о режимах шифрования и имитовставки
- •Глава 6. ВЫБОР ДОЛГОВРЕМЕННОГО КЛЮЧА АЛГОРИТМА ГОСТ 28147-89
- •6.1. Область сильных ключей
- •6.1.1. Достаточность условия равновероятности псевдогаммы для выбора сильного блока подстановки
- •6.2. Контроль долговременного ключа алгоритма ГОСТ 28147-89
- •6.2.1. Угроза внедрения слабых параметров
- •6.2.2. Подход к выявлению слабых долговременных ключей
- •6.2.3. Свойства теста
- •6.2.4. Тестирование долговременного ключа
- •Глава 7. ЭЛЕМЕНТЫ ТЕОРИИ СРАВНЕНИЙ
- •7.1.1. Расширенный алгоритм Эвклида
- •7.2. Модульная арифметика
- •7.2.1. Функция Эйлера и малая теорема Ферма
- •7.3. Сравнения первой степени от одного неизвестного
- •7.3.1. Китайская теорема об остатках
- •7.3.2. Степенные сравнения по простому модулю
- •Глава 8. ВЫЧИСЛЕНИЕ КВАДРАТНОГО КОРНЯ В ПРОСТОМ ПОЛЕ
- •8.1.1. Символ Лежандра
- •8.1.2. Символ Якоби
- •8.2. Алгоритм нахождения квадратного корня в простом поле
- •9.1. Построение криптосистемы RSA. Идея цифровой подписи
- •9.2. Смешанные криптосистемы. Протокол Диффи-Хэллмана ключевого обмена
- •9.3. Цифровая подпись Эль-Гамаля
- •9.3.1. Криптосистема Эль-Гамаля
- •9.3.2. Механизм цифровой подписи Эль-Гамаля
- •9.3.3. Ослабление подписи Эль-Гамаля вследствие некорректной реализации схемы
- •9.3.4. Варианты цифровой подписи типа Эль-Гамаля
- •10.1 Обозначения и постановка задачи
- •10.2. Построение корней из единицы в поле
- •10.3. Алгоритм дискретного логарифмирования
- •10.3.1. Пример вычисления дискретного логарифма
- •10.4. Фальсификация подписи Эль-Гамаля в специальном случае выбора первообразного элемента и характеристики поля
- •10.4.1. Слабые параметры в подписи Эль-Гамаля
- •Глава 11. МЕТОДЫ ФАКТОРИЗАЦИИ ПОЛЛАРДА
- •11.2.1. Оценка вероятности выбора критической пары
- •11.2.2. Оптимизация выбора критической пары
- •Глава 12. НЕКОТОРЫЕ СЛУЧАИ ОСЛАБЛЕНИЯ КРИПТОСИСТЕМЫ RSA
- •12.1. Атаки на RSA, не использующие факторизацию модуля
- •12.2. Атаки на RSA, использующие факторизацию модуля
- •12.2.1. Алгоритм факторизации Диксона
- •Глава 13. ТЕСТ ФЕРМА ПРОВЕРКИ ЧИСЕЛ НА ПРОСТОТУ
- •13.1. Решето Эратосфена и критерий Вильсона
- •13.2. Тест на основе малой теоремы Ферма
- •13.2.1. Основные свойства псевдопростых чисел
- •13.2.2. Свойства чисел Кармайкла
- •13.2.3. (n-1) - критерий Люка
- •13.2.3. Понятие о последовательностях Люка. (n+1) - критерий Люка
- •Глава 14. ТЕСТЫ СОЛОВЕЯ-ШТРАССЕНА И РАБИНА-МИЛЛЕРА ПРОВЕРКИ ЧИСЕЛ НА ПРОСТОТУ
- •14.1. Тест Соловея-Штрассена
- •14.1.1. Эйлеровы псевдопростые числа
- •14.2. Тест Рабина-Миллера
- •14.2.1. Сильно псевдопростые числа
- •Глава 15. ПОСТРОЕНИЕ БОЛЬШИХ ПРОСТЫХ ЧИСЕЛ
- •15.1. Детерминированный тест, основанный на обобщенном критерии Люка
- •15.1.1. Теорема Поклингтона
- •15.1.2. Обобщение критерия Люка
- •15.2. Детерминированный тест, основанный на теореме Димитко
- •Глава 16. ВЫБОР ПАРАМЕТРОВ КРИПТОСИСТЕМЫ RSA
- •16.1. Общие требования к выбору параметров
- •16.2. Метод Гордона построения сильно простых чисел
- •16.3. Пример построения сильно простого числа
- •Глава 17. ОБЩИЕ СВЕДЕНИЯ ОБ ИНОСТРАННЫХ КРИПТОСРЕДСТВАХ
- •17.1. Аппаратные криптосредства
- •17.2. Основные принципы построения систем управления ключами
- •17.2.1. Ключевые системы потоковых шифров
- •17.3. Блочные шифры в смешанных криптосистемах
- •17.3.2. Смешанная криптосистема на основе алгоритмов RSA и IDEA
- •ЗАКЛЮЧЕНИЕ
- •ЛИТЕРАТУРА

130 Глава 10. АЛГОРИТМ СИЛЬВЕРА - ПОЛЛИГА - ХЭЛЛМАНА
Запись показателя в виде дроби корректна, поскольку один из сомножителей числителя, а именно u , делится на p , т.е. дробь является обычным целым числом.
Очевидно, rpp, j =b ju =1, следовательно, элементы rp, j - корни степени p
из единицы. Аналогичным образом заполним все строки таблицы R .
Дальнейшая работа сводится к вычислениям, в результате которых появляются элементы, являющиеся корнями степени p из единицы в поле.
Для каждого такого элемента будет необходимо определить его позицию
j (номер колонки) в строке таблицы R с меткой |
p . |
|
|
|
||||
Поскольку в каждой строке элементы различны, то для данного числа |
||||||||
соответствующую ему позицию мы определим однозначно. |
|
|
||||||
Для этого, |
конечно, мы должны быстро просмотреть строку таблицы R , |
|||||||
что возможно, поскольку число q −1 - гладкое. |
|
|
|
|
||||
10.3. Алгоритм дискретного логарифмирования |
|
|
||||||
Предположим, что x представлен в |
p -ичной системе счисления. Тогда |
|||||||
его вычет по |
модулю pa |
имеет вид |
x = x |
+ x p +K+ x |
a−1 |
pa−1 mod pa , |
||
|
|
|
|
0 |
1 |
|
|
|
0 ≤ xi ≤ p −1. |
|
|
|
|
|
|
|
|
Обозначим |
y0 = y . |
Для |
определения |
чисел |
xk , |
k = 0,K,a −1, |
||
предложим следующую процедуру, которую обсудим позже. |
|
|
||||||
Прежде всего, определяем x |
как позицию |
yu p |
в строке с номером p |
|||||
|
|
0 |
|
|
0 |
|
|
|
таблицы R .

Алгоритм дискретного логарифмирования 131
Для |
k >0 коэффициент xk |
определяем как позицию элемента |
yku |
pk +1 |
в |
|||||||||||||||||||
строке |
с |
меткой |
p |
|
таблицы |
R . |
При |
этом, |
yk = y0 |
bh(k ) , |
где |
|||||||||||||
h(k )= x + x p +K+ x |
pk −1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
1 |
k −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Повторив процедуру |
|
|
для |
каждого |
p , |
|
делящего |
q −1, |
мы |
получаем |
||||||||||||||
значения |
|
x mod pa , |
а затем |
с |
|
помощью китайской |
теоремы |
об |
остатках |
|||||||||||||||
восстанавливаем x mod(q −1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Обоснуем процедуру определения xk . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Вычислим y0u p . Очевидно, |
y0u p - |
корень степени |
p из единицы, причем |
|||||||||||||||||||||
yu p = yu |
p = bxu p = bx0u p+(x−x0 )u |
p |
, где |
x − x |
0 |
= x p +K+ x |
a−1 |
pa−1 . |
|
|
|
|||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
Кроме того, число x0u |
|
|
p является целым, т.к. u делится на |
p . |
|
|
|
|
||||||||||||||||
В выражении (x − x0 )u p оба сомножителя делятся на |
p . Разделив на |
p |
||||||||||||||||||||||
первый |
сомножитель, |
получаем, |
что (x − x |
)u |
p = ku , |
т.е. |
|
yu |
p |
= bx0u |
p . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
Сравнив с обозначением r |
|
, j |
=b ju |
p , получаем, что yu p |
= r |
|
при |
j = x . |
|
|||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
0 |
p, j |
|
|
|
|
0 |
|
|
||||
Это позволяет определить |
x |
, как позицию |
yu p в строке таблицы |
R с |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
меткой p . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уничтожим теперь x |
|
|
в показателе степени bx , |
разделив |
y |
0 |
на |
bx0 . |
||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Обозначим результат через y1 : y1 = y0  bx0 p0 и вычислим y1u
bx0 p0 и вычислим y1u p2 =bu(x−x0 )
p2 =bu(x−x0 ) p2 .
p2 .
По условию, число u p2 |
- целое (при a ≥ 2). В выражении |
x − x |
все |
||||
|
|
|
|
|
|
0 |
|
члены, кроме |
x p , делятся на |
p2 . Поэтому в показателе |
u (x − x |
|
) |
p2 |
все |
|
1 |
|
0 |
|
|
|
|
члены, кроме ux1 p p2 , кратны u и на значение bu(x−x0 ) p2 не влияют.
p2 , кратны u и на значение bu(x−x0 ) p2 не влияют.

132 Глава 10. АЛГОРИТМ СИЛЬВЕРА - ПОЛЛИГА - ХЭЛЛМАНА
|
Поскольку u делится на |
p , |
то число |
ux p |
p2 |
=x u |
p - |
также целое, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
откуда yu |
p2 = bx1u p = r |
при |
j = x . Таким образом, |
x равен позиции |
yu p2 |
|||||||||||||
|
1 |
|
p, j |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
в строке с меткой p таблицы R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Для определения |
x |
уничтожим |
x |
в показателе степени bx−x0 , разделив |
|||||||||||||
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
y |
на |
bx1 p1 . |
Получим: |
y |
2 |
= y |
0 |
bx0 p0 +x1 p1 |
, |
т.е. |
y |
2 |
= bd , |
где |
||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
d = x2 p2 +K+ xa−1 pa−1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Вычисляем yu p3 |
= bx2u p = r |
, при |
j = x , что позволяет определить x |
||||||||||||||
|
|
2 |
|
|
p, j |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
по таблице R и т.д., пока не определим xa−1 . |
|
|
|
|
|
|
|
|
||||||||||
|
10.3.1. Пример вычисления дискретного логарифма |
|
|
|
|
|||||||||||||
|
В поле F37 , при b = 2, найти дискретный логарифм элемента 28. |
|
||||||||||||||||
|
Решение. Задача сводится к решению в поле F |
|
уравнения 28 = 2x . |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
37 |
|
|
|
|
|
|
|
|
Число |
q = 37 |
является |
первой |
|
степенью |
простого |
числа, поэтому |
||||||||||
операции в поле совпадают с операциями в поле вычетов по модулю 37, в частности, деление есть умножение на обратный элемент.
|
Далее, |
u = q −1 =36 = 22 32 , |
|
следовательно, |
имеем два |
простых |
|||||
делителя: 2 и 3. |
|
|
|
|
|
|
|
|
|
||
|
Составим таблицу |
R . |
Начнем |
со строки с меткой p = 2. |
Вычислим |
||||||
r |
=b j(q−1) 2 |
для j = 0,1 |
: r |
|
=1, |
r |
|
= 2(q−1) 2 ≡ −1(37). |
|
|
|
2, j |
|
|
2,0 |
|
2,1 |
|
|
|
|
||
|
Элементами строки с меткой 3 |
являются числа: |
r |
=b j(q−1) 3 , |
j = 0,1,2 , |
||||||
|
|
|
|
|
|
|
|
|
3, j |
|
|
т.е. r3,0 =1, r3,1 = 236 3 ≡ 26(37), r3,2 = 22 36
3 ≡ 26(37), r3,2 = 22 36 3 ≡ 224 ≡10(37). Таблица R имеет следующий вид.
3 ≡ 224 ≡10(37). Таблица R имеет следующий вид.
Алгоритм дискретного логарифмирования 133
Таблица 4. Корни из единицы степеней 2 и 3
0 1 2
R= 2 1 -1 0
3 |
1 |
26 |
10 |
Найдем вычет |
x = x |
+ x p +K+ x |
a−1 |
pa−1 |
mod pa , |
при p = 2, a = 2 . |
|
0 |
1 |
|
|
|
|
Число шагов равно |
a = 2 . Итак, необходимо определить |
x0 , x1 . Найдем x0 . |
||||
Вычислим y0u p = 2818 ≡1(37). Позиция единицы в строке 2 таблицы R равна
p = 2818 ≡1(37). Позиция единицы в строке 2 таблицы R равна
0, следовательно, x0 = 0 .
Далее будем вычислять элементы yk и возводить их в степени u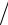 pk+1 .
pk+1 .
Вычислим y , |
уничтожив член с |
x |
в показателе числа bx : |
y = y |
0 |
bx0 p0 . |
|||||||||
|
1 |
|
|
|
|
0 |
|
|
|
1 |
|
|
|||
Поскольку x |
= 0 , |
то y = y . |
Возводим y |
в степень u |
p2 , |
где |
|
|
p2 = 4: |
||||||
0 |
|
1 |
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
yu 4 = 2836 4 = −1(37). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Позиция числа (-1) в строке 2 таблицы R равна 1, следовательно, |
|
x1 =1. |
|||||||||||||
Итак x = x0 + x1 p = 2 mod 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдем вычет |
x mod pa , при |
p = 3 , a = 2 . Число шагов равно a = 2 . |
|||||||||||||
y0u p = 2812 ≡ 26(37). Позиция |
числа |
26 в строке 3 таблицы |
R |
равна 1, |
|||||||||||
следовательно, |
x =1, поэтому |
y = y |
0 |
bx0 p0 =14 . |
|
|
|
|
|
|
|
||||
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Возводим |
y |
в степень |
u |
p2 , |
где |
p2 =9 : |
yu 9 |
=1436 9 =10(37), |
|||||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
следовательно x1 = 2 . Итак, |
x =7 mod9. |
|
|
|
|
|
|
|
|
||||||

134 Глава 10. АЛГОРИТМ СИЛЬВЕРА - ПОЛЛИГА - ХЭЛЛМАНА
Решаем |
систему сравнений x = 2 mod4 , x =7 mod9: 9−1(4)=1, |
4−1(9)=7 , |
x ≡ 2 9 (9−1 mod 4)+ 7 4 (4−1 mod 9)= 214 , т.е. |
x ≡34 mod36 .
10.3.2. Логарифмирование в группе единиц кольца вычетов по модулю pr.
Существование частных методов дискретного логарифмирования в конечном поле приводит к необходимости построения больших простых чисел со специальными свойствами. В качестве подхода, позволяющего снизить величины генерируемых простых чисел, можно, в принципе, рассмотреть использование в протоколе Диффи-Хэллмана операцию приведения по модулю
pr , p > 2, r >1. В |
этом случае |
легко обеспечить большие размеры и |
разнообразие генерируемых ключей. |
|
|
Известно [14,гл.6], |
что в кольце |
Z pr Z вычетов по модулю m = pr |
существует первообразный элемент γ , степени которого представляют все вычеты, взаимно простые с модулем. Эти вычеты образуют в  мультипликативную группу U(pr )из ϕ(pr )элементов (т.н. группу единиц).
мультипликативную группу U(pr )из ϕ(pr )элементов (т.н. группу единиц).
Можно показать [20,гл.4], что если γ p - первообразный корень в поле
GF(p), то одно из чисел γ =γ p + kp , где k {0,1}, удовлетворяет условию
(γ p + kp)p−1 ≠1(mod p2 )и является первообразным корнем по любому модулю pα , α >1. Заметим, что пары чисел a, p, для которых выполняется соотношение a p−1 =1mod p2 , встречаются редко. Поэтому будем считать, что
γ =γ p .
Таким образом, любой из ϕ(pr )= pr−1(p −1) вычетов b U (pr ) можно
представить в виде b =γ x mod pr .

Алгоритм дискретного логарифмирования в группе единиц… 135
Соответственно, задача дискретного логарифмирования в группе единиц кольца Z pr Z состоит в определении вычета x по modϕ(pr ), исходя из b и
pr Z состоит в определении вычета x по modϕ(pr ), исходя из b и
γ .
К сожалению, использование модуля pr не дает преимуществ, поскольку
при наличии эффективного алгоритма логарифмирования в простом поле
GF(p) логарифмирование в группе единиц кольца вычетов по модулю pr , r >1, практически всегда можно осуществить, воспользовавшись свойствами так называемого обобщенного отношения Ферма Lm (a) [21,46].
Областью определения отображения Lm (a) является группа U (m)
вычетов по модулю m, взаимно простых с модулем. По теореме Эйлера,
существует λ : aϕ(m ) −1 = λm . Значение Lm (a) определяется как вычет числа λ по модулю m: Lm (a)= aϕ(mm) −1(mod m).
Легко убедиться, что отношение Ферма обладает следующими замечательными свойствами.
Lm (ab)= Lm (a)+ Lm (b)(modm),
Lm (a + mc)= Lm (a)+ϕ(m)ca-1 (mod m),
где a,b U (m), c Z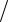 mZ .
mZ .
|
Далее будем считать, что m = pr , |
r >1. Заметим, |
что в этом случае, |
|||
L |
(a + mc)= L (a)+ (pr − pr−1 )ca-1 (mod m)= L (a)(mod pr−1 ). |
Таким |
||||
m |
|
m |
|
m |
|
|
образом, если a ≡ b(mod m), то |
L (a)≡ L (b)(mod pr−1 ). |
|
||||
|
|
|
m |
m |
|
|
|
Если |
L (γ )= 0(mod pr−1 ), |
то из |
определения |
L (γ ) следует, что |
|
|
|
m |
|
|
m |
|
γϕ(m) =1(mod p2r−1 ).

136 Глава 10. АЛГОРИТМ СИЛЬВЕРА - ПОЛЛИГА - ХЭЛЛМАНА
Однако, |
γ |
- первообразный |
корень по |
любому |
модулю |
pα , α >1, |
||||||||
поэтому ϕ(p2r−1 )≤ϕ(m), |
откуда |
2r − 2 ≤ r −1, т.е. |
r ≤1, что противоречит |
|||||||||||
условию. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если L |
(γ )= 0(modm), то |
L |
(γ )= 0(mod pr−1 )и r ≤1. |
|
|
|||||||||
|
m |
|
|
|
|
m |
|
|
|
|
|
|
|
|
Аналогично, при L |
|
(γ )= pt(mod pr−1 ), |
получаем |
γϕ(m) =1(mod pr+1 ), |
||||||||||
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
что невозможно, т.к. ϕ(pr+1 )>ϕ(m). |
|
|
|
|
|
|
|
|||||||
Таким образом, элемент Lm (γ ) |
взаимно |
прост |
с |
p и, следовательно, |
||||||||||
обратим по модулю pr−1 . |
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим задачу логарифмирования |
в группе единиц кольца |
Z mZ , |
||||||||||||
полагая, |
что |
эффективный алгоритм |
логарифмирования в кольце |
Z pZ |
||||||||||
известен. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из соотношения b =γ x mod pr |
следует, |
что |
b =γ x mod p , |
т.е. нам |
||||||||||
известно значение x по модулю |
p −1. Если мы найдем x(mod pr−1 ), то |
|||||||||||||
значение |
x |
по модулю ϕ(m)= pr−1(p −1) |
можно вычислить по китайской |
|||||||||||
теореме об остатках. |
|
|
|
|
|
|
|
|
|
|
|
|||
Очевидно, |
что значение x(mod pr−1 ) |
легко определить |
из сравнения |
|||||||||||
L (b)= xL (γ )(mod pr−1 ). |
|
|
|
|
|
|
|
|
|
|||||
m |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким |
|
образом, |
|
нам |
|
необходимо |
вычислять |
значения |
||||||
h = Lm (a)(mod pr−1 ).
