ЛЕКЦІЯ 13 ПРОТОКОЛИ ДЕПОНУВАННЯ БІТУ

У ході деяких процедур обміну інформацією з недовірою між учасниками виникає необхідність передати від абонента (відправник) до абонента (отримувач) дані, які, з одного боку, мають бути недосяжні для деякий проміжок часу, а з іншого боку, потрібно, щоб абонент не міг оперувати модифікованою копією цих даних під час виконання процедури.

До цієї задачі можна підійти таким чином.

На першому етапі готує повідомлення і надсилає значення , де функція відіграє роль «конверта» для , який не може відкрити без допомоги .

На другому етапи, в потрібний час, «відкриває» значення , тобто надає інформацію , що дозволяє «відкрити конверт», але при цьому не може впливати на результат, за рахунок .

Виходячи з цього, надійність протоколу депонування (вручення) біту розділяється на надійність відносно отримувача та надійність відносно відправника.

Надійність відносно отримувача: не може отримати до завершення другого етапу.

Надійність відносно відправника: якщо протокол завешено успішно, отримане значення істинне.

Очевидно, достатньо розглянути відповідний протокол для одного біту, тобто для .

13.1 Протокол вручення біту на основі симетричної криптосистеми

Параметри та деякі позначення:

- параметр надійності;

розмір в бітах;

- біт, що має бути депонований;

- симетрична криптосистема з множиною ключів , алгоритмом зашифрування і алгоритмом розшифрування .

Таблиця 13.1 Вручення біту на основі симетричної криптосистеми

Перший етап протоколу
1.				Отримувач надсилає випадкову послідовність довжини , щоб відправник не міг маніпулювати ключами шифрування на кроках 2 і 3.
2.				У даному випадку,
Другий етап протоколу
3.				перевіряє, чи , якщо так, то приймається.

13.2 Протокол вручення біту на основі геш-функції

Параметри та деякі позначення:

- параметр надійності;

- криптографічно стійка геш-функція з довжиною геш-коду ;

- біт, або декілька бітів, що мають бути депоновані.

- симетрична криптосистема з множиною ключів , алгоритмом зашифрування і алгоритмом росшифрування .

Таблиця 13.2 Протокол вручення біту на основі геш-функції

Перший етап протоколу
1.		,	,	Отримувач не знає і не може обчис-лити геш-код самостійно. У даному випадку,
Другий етап протоколу
1.				перевіряє, чи , якщо так, то приймається.

Цей протокол не є інтерактивним, всі повідомлення виходять від .

13.3 Протокол вручення біту на основі односпрямованого гомоморфізму

- гомоморфізм груп, якщо .

Параметри та деякі позначення:

- групи;

- гомоморфізм груп, що вважається одностороннім відобра-женням;

- біт, що має бути депонований;

- множина елементів групи без одиниці групи.

Таблиця 13.2 Протокол вручення біту на основі гомоморфізму

Перший етап протоколу
1.				Отримувач надсилає випадковий елемент, щоб відправник не міг маніпулювати значенням на кроках 2 і 3.
2.			,	У даному випадку,
Другий етап протоколу
3.				перевіряє, чи , якщо так, то приймається.

Приклад. Нехай і - велики секретні прості числа:, а - первісний корень в . Нехай також .

Оскільки функція Ейлера , то показник в обчислюється за модулем . Таким чином, .

13.4 Протоколи кидання монети

Мета протоколу протоколів кидання монети - імітувати на ЕОМ вибір випадкового значення біту , що після завершення протоколу є відомим для обох учасників. Тобто, незалежно від поведінки учасників, при успішному завершенні протоколу, .

13.4.1 Протокол кидання монети з використанням протоколу депонування бітів

Параметри та позначення:

- протокол депонування біту;

- - результат першого етапу протокол депонування.

Таблиця 13.3 Кидання монети на основі протоколу депонування біту

1.				Відправник виконує перший етап протоколу депонування біту
2.
3.				розкриває значення
4.				і обчислюють значення випадко-вого біту

Очевидно, при наявності протоколу депонування бітів задача кидання монети вирішується з надійністю протоколу депонування.

13.4.2 Протокол кидання монети з використанням функції Рабіна

Функції Рабіна – це одностороння функція піднесення до квадрату за модулем великого біпростого числа , - секретні великі нерівні прості числа.

Обчислення оберненої функції (дискретний квадратний корень за модулем ) вимагає факторизації модуля.

Якщо відомі, то можна спочатку обчислити квадратні корені , , , скажемо, з за модулями окремо:

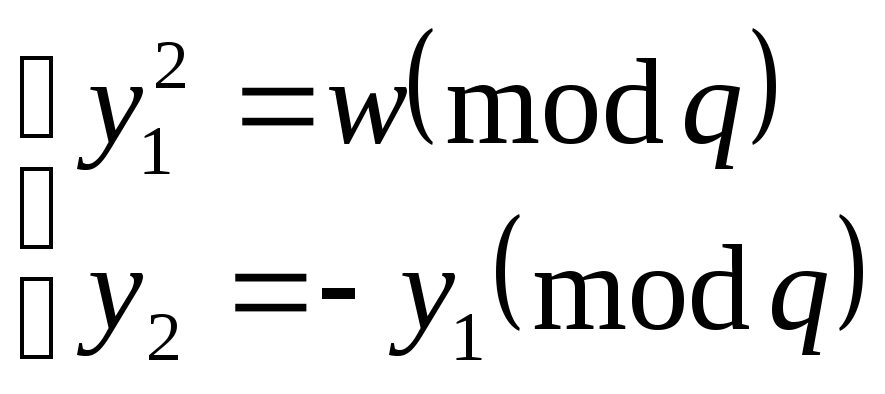
а потим відновити корені : , використовуючи Китайську теорему про залишки для кожної з чотирох систем порівнянь:

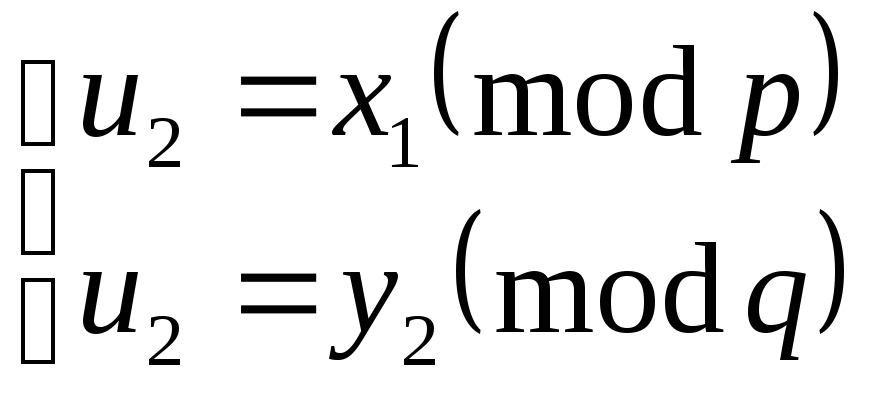
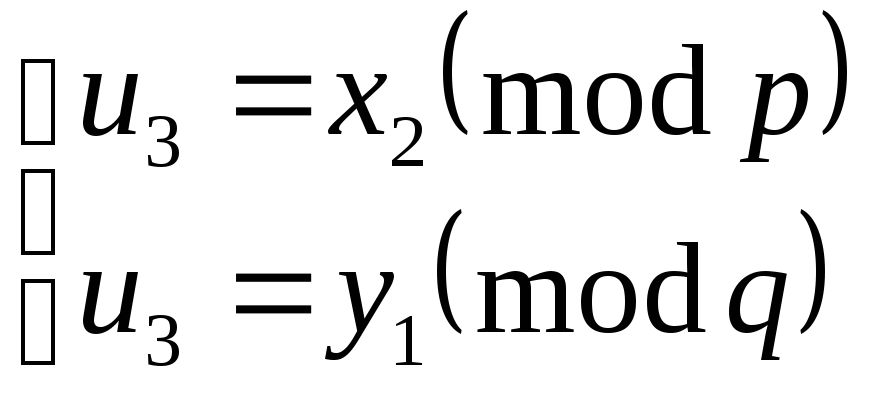
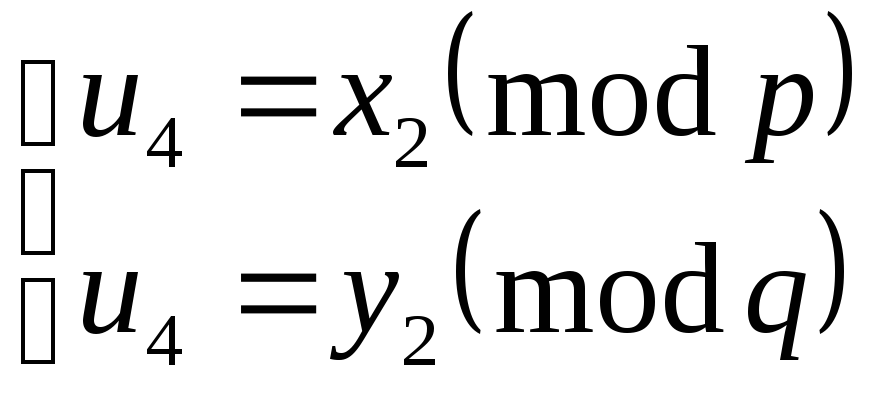
Якщо - корень за , то також корень за , тобто, якщо розглядати лишки як ціли числа, з пари коренів один корень менший за , а інший - більший. Розібємо корені на дві такі пари, та позначимо менші корені (з кожної пари свій) через .

При цьому, очевидно, , а співпадіння розрядів у кожній з позицій двійкового запису коренів є випадковим.

Для опису протоколу позначимо через значення біта номер при записі у системі счислення за основою два (відлік бітів справа наліво). У протоколі задіяні учасники і .

Таблиця 13.4 Кидання монети на основі функції Рабіна

1				будує - секретні великі нерівні прості числа, а також .
2.			,	Отримувач надсилає квадратичний лишок , при випадко-вому виборі значення квадратного кореня .
3.			, ,	також здійснює випадковий вибір одного з коренів з умовою . Для цього він, виходячи з , знаходить корені , відбирає з них , та знаходить мінімальний номер позиції двійкового представленя у якій видповідні біти цих коренів не співпадають. Далі він вибирає випадково , обчис-лює біт і надсилає його . Зауважимо, що не знає .
4.			Перевірка співвідно-шень ,	надсилає інформацію, необхідну для виконання п.6, оскільки вже невзмозі впливати на результат протоколу. перевіряє, чи дійсно є одним з коренів .
5.				надсилає інформацію, необхідну для виконання п.6, оскільки вже невзмозі впливати на результат протоколу.
6.			Спільним результатом кидання монети є	1. є одним з двох коренів . Таким чином, і реалізують випадковий незалежний вибір значень розрядів з номером коренів . Значення розряду номер коренів гарантовано не співпадають, тобто порозрядна сума цих значень при випадковому виборі є випад-ковим бітом. 2. На даному етапі знає (див. п.5), тому він може обчислити і, як наслідок, , і потім біт . для обчислення біта достатньо знати .

5