Особливі точки та їх класифікація

Приклад. Знайти всі особливі точки функції та визначити їх характер:

.

Розв’язання. Знайдемо точки, де функція не визначена: ,,,,,. Дослідимо поведінку функції в околі кожної з цих точок.

:

;

–усувна особлива точка.

: ;

; – полюс другого порядку.

: ;

;

–простий полюс.

: ;

;

–простий полюс.

: – не

існує, оскільки не існує ;

–істотно особлива точка.

: – не

існує, оскільки не існує ;

–істотно особлива точка.

Лишки та їх застосування

Приклад. Обчислити вказані лишки:

а) ; б);

в) ;г) ; д) .

Розв’язання. 

а) Для функції точка – усувна особлива, оскільки

.

Тому .

б) Для функції точка – простий полюс, оскільки

;

.

Тому .

в) Для функції точка – полюс другого порядку, оскільки

;

.

Тому

.

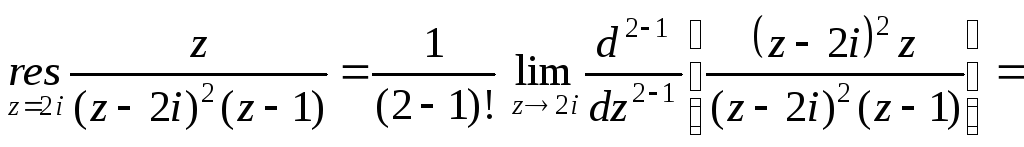
г) Для функції точка – істотно особлива, оскільки не існує ні скінченної, ні нескінченної границі . Знайдемо ряд Лорана:

; ;

.

Тому .

д) Для функції точка – істотно особлива, оскільки не існує ні скінченної, ні нескінченної границі . Знайдемо ряд Лорана:

;

.

Тому

.

Обчислення інтегралів за допомогою лишків

Приклад 1. Обчислити комплексний інтеграл

,

де а) ; б).

Розв’язання. 

Підінтегральна функція має три особливі точки(самостійно переконайтеся в цьому і дослідіть їх характер): – полюс третього порядку,– простий полюс,– істотно особлива точка ((рис. 32).

а) Усередині коларозміщена тільки одна особлива точка – полюс третього порядку. За основною теоремою про лишки

;

;

.

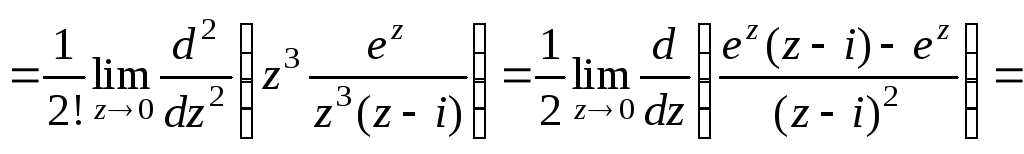
б) Перший спосіб. Усередині кола розміщені дві особливі точки – полюс третього порядку і– простий полюс. За основною теоремою про лишки

;

;

.

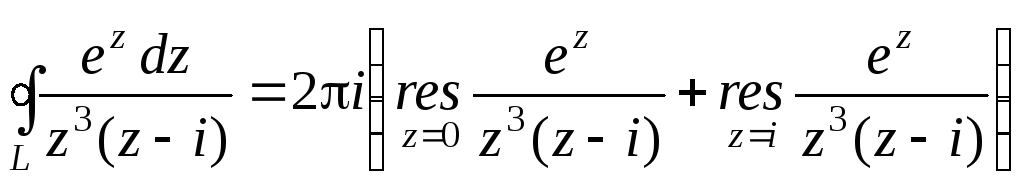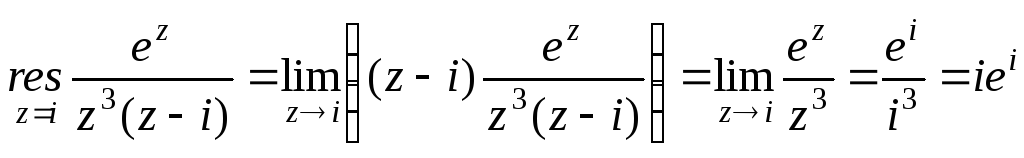Другий спосіб. Зовні кола розміщена тільки одна особлива точка – істотно особлива. За наслідком 2 із основної теореми про лишки

.

Розвинемо підінтегральну функцію в ряд Лорана:

;

;

.

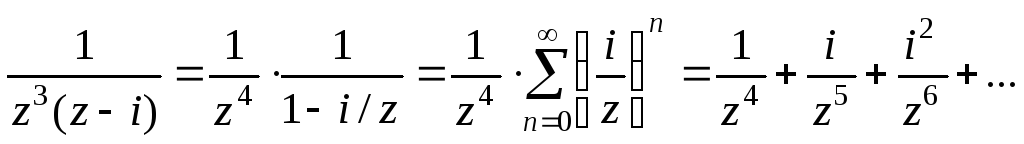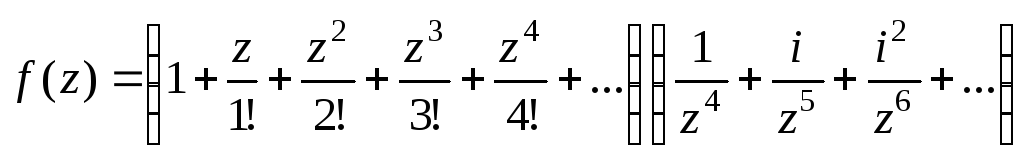Звідси

; .

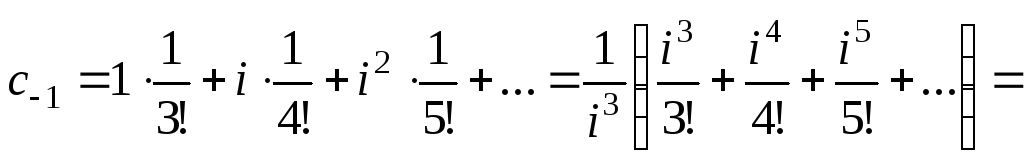
Тоді

.

Приклад 2. Обчислити дійсний невласний інтеграл

.

Розв’язання. Підінтегральна функція не­пе­рервна на дійсній осі, а відповідна комплексна функціяаналітична у верхній півплощині за винятком однієї особливої точки – полюса другого порядку. Крім того, при .Знайдемо лишок:

.

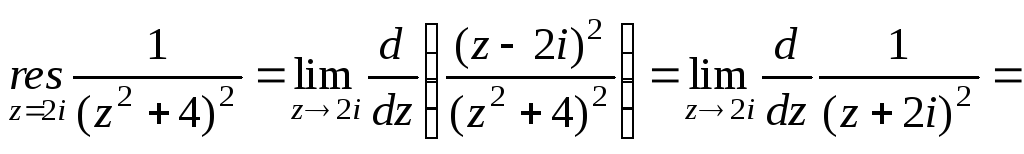
Тоді за наслідком леми Жордана (при )

.

Приклад 3. Обчислити дійсний невласний інтеграл

.

Розв’язання. Застосуємо заміну .

Відповідна комплексна функція у верх­ній півплощині має одну особливу точку – простий по­люс. Знайдемо лишок:

.

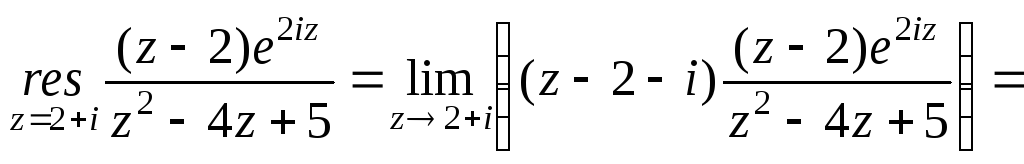
Тоді, виділяючи дійсну частину, за наслідком леми Жордана отримаємо

.

Завдання на СРС

Завдання 1. Обчислити заданий інтеграл по замкненому контуру від аналітичної функції за допомогою лиш­ків.

№ в-та		№ в-та
1	;	16	;
2	;	17	;
3	;	18	;

Заключення: На цьому занятті ми з Вами набули первинних навичок інтегрування функцій комплексної змінної. Ви зможете закріпити здобуті навички виконуючи завдання для самостійної роботи. Отже, мета практичного заняття досягнута.

Методична розробка виконана: професором кафедри ВМ

Онищенко В.В.________________