
Міністерство освіти і науки України
Державний університет ТеЛЕКОМУНІКАЦІЙ
КАФЕДРА ВИЩОЇ МАТЕМАТИКИ
ЗАТВЕРДЖУЮ
Завідуючий кафедрою
________________Барабаш О.В.
“ ____ “ _____________ 2015 року
Тільки для викладачів
СЕМЕСТР 2
МЕТОДИЧНА РОЗРОБКА № 17(35)
МОДУЛЬ 3(6)
Тема 5(12): Основи теорії функції комплексної змінної.
Розклад функцій в ряд Лорана. Особливі точки та інтегральні лишки аналітичних функцій.
з навчальної дисципліни вища математика
напряму підготовки телекомунікації
освітньо-кваліфікаційного рівня бакалавр
Розробка
кандидатом фіз.-мат. наук, доцентом Онищенко В.В.
Обговорено на засіданні кафедри (ПМК)
Протокол № __________
“ ____ “ _____________ 2015 року
Київ - 2015
Навчальні цілі: Набуття студентами первинних навичок розкладу функцій в ряд Лорана. Знаходити особливі точки та інтегральні лишки аналітичних функцій.
Виховні цілі: Обґрунтувати, що якісне вивчення математичного програмування сприяє:
розвитку логічного та аналітичного мислення, пам’яті;
можливості самостійно вивчати сучасну науково-технічну літературу;
вмінню коротко і зрозуміло висловлювати свої думки;
акуратності і точності записів, уважності, дисциплінованості;
вмінню конспектувати, красиво оформлювати записи робочих зошитів для практичних занять та індивідуальних робіт;
набуттю навичок систематизації матеріалу, що вивчається.
Час: 1,5 години.
План проведення заняття та розрахунок часу
Введення.
Перевірити наявність студентів…………………………….……до 5 хвилин
Навчальні питання:
1.Актуалізація знань студентів ………………………………10 хвилин
2.Оримання практичних навичок 55 хвилин
3.Завдання………………………………………………………….. 15 хвилин
Заключення до 5 хвилин
НАВЧАЛЬНО-МАТЕРІАЛЬНЕ ЗАБЕЗПЕЧЕННЯ
Бажано мати:
1. крейду і вологу губку.
Література:
1. Пискунов Н. С. Дифференциальное и интегральное исчисление. – М.: Наука, 1978. – Т.2.
Гутер Р.С., Янпольский А.Р. Дифференциальные уравнения: Учебное пособие для втузов. – Изд.2-е, перераб. и доп. – М.: Высшая школа, 1976.
Данко П. Е., Попов А. Г. Высшая математика в примерах и задачах: Учебное пособие, ч. 2. – М.: Высшая школа, 1967.
Берман Г. Н. Сборник задач по курсу математического анализа для втузов. – М.: Наука, 1972.
Демидович Б. П. Сборник задач и упражнений по математическому анализу: Учебное пособие для вузов. – 10-е издание. – М.: Наука,1990.
Валєєв К. Г., Джаладова І. А., Лютий О.І. та ін. Вища математика: Навч.-метод. посібник для самост. вивч. дисц. – К.: КНЕУ, 2002.
Навчальні матеріали
І. Актуалізація знань студентів (повторення основних положень лекції):
Ряди функцій комплексної змінної
Приклад 1. Дослідити на збіжність:
а)
![]() ; б)
; б)
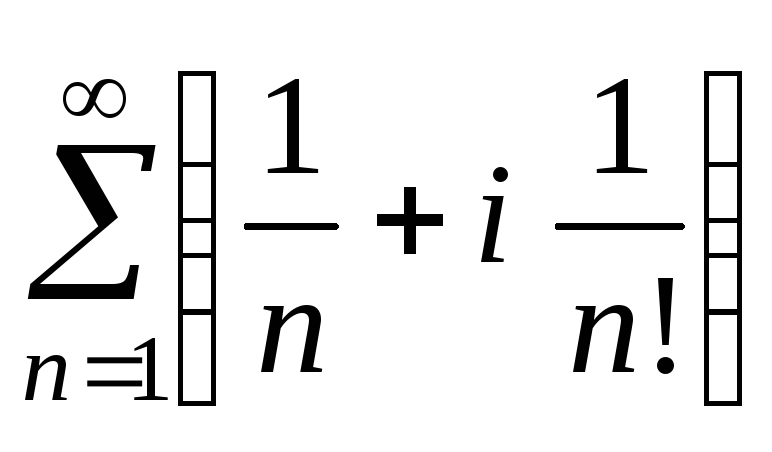 ;
;
в)
![]() ; г)
; г)
![]() .
.
Розв’язання.
а)
Обидва дійсні ряди
![]() і
і![]() збігаються
– перший за ознакою Даламбера, а другий
за радикальною ознакою Коші (покажіть
це самостійно). Тому заданий ряд
збігаються
– перший за ознакою Даламбера, а другий
за радикальною ознакою Коші (покажіть
це самостійно). Тому заданий ряд
![]() також збігається.
також збігається.
б)
Ряд з дійсних частин
![]() розбігається як гармонічний, тому
заданий ряд
розбігається як гармонічний, тому
заданий ряд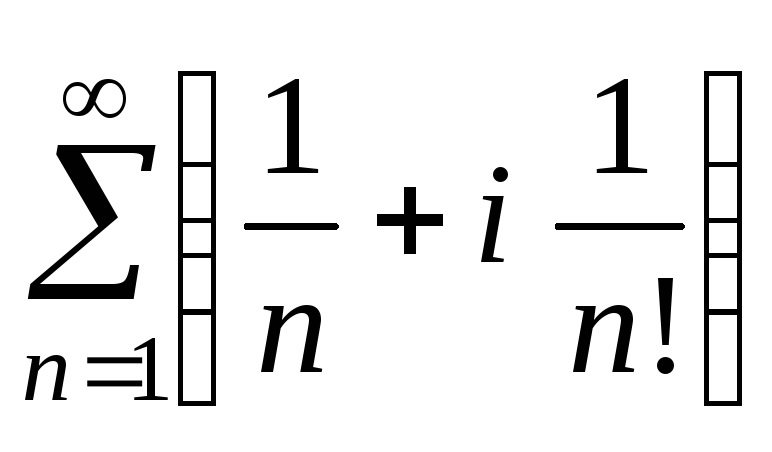 теж розбігається (хоча ряд з уявних
частин
теж розбігається (хоча ряд з уявних
частин![]() збігається заознакою
Даламбера).
збігається заознакою
Даламбера).
в)
Ряд з дійсних частин
![]() збігається як узагальнений гармонічний
з показником степеня
збігається як узагальнений гармонічний
з показником степеня![]() ,
а ряд з уявних частин
,
а ряд з уявних частин![]() розбігається як геометрична прогресія
зі знаменником
розбігається як геометрична прогресія
зі знаменником![]() .
Тому заданий ряд
.
Тому заданий ряд![]() теж розбігається.
теж розбігається.
г)
Обидва дійсні ряди
![]() і
і![]() розбігаються,
оскільки не задовольняють необхідну
ознаку збіжності (покажіть це
самостійно). Тому заданий ряд
розбігаються,
оскільки не задовольняють необхідну
ознаку збіжності (покажіть це
самостійно). Тому заданий ряд
![]() також розбігається.
також розбігається.
Приклад 2. Показати, що заданий ряд збігається абсолютно
![]() .
.
Розв’язання. Дослідимо на збіжність ряд із модулів:
![]() .
.
Цей
ряд збігається
як геометрична прогресія зі знаменником
![]() .
Тому заданий ряд
.
Тому заданий ряд![]() збігається
абсолютно.
збігається
абсолютно.
Приклад 1. Знайти радіус збіжності степеневого ряду:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Розв’язання.
а)
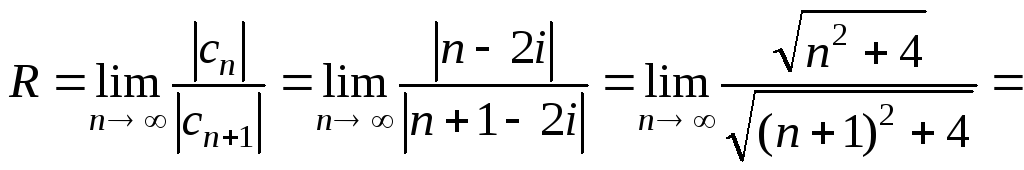
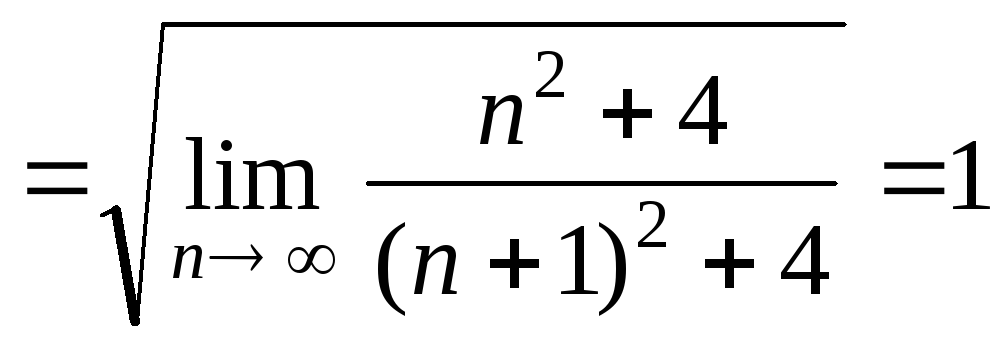 .
.
б)
![]() .
.
в)
![]()
![]() .
.
Приклад 2. Розкласти
функцію
![]() в ряд Тейлора в околі точки
в ряд Тейлора в околі точки
![]() і знайти радіус збіжності отриманого
ряду.
і знайти радіус збіжності отриманого
ряду.
Розв’язання. Подамо функцію у вигляді
![]()
![]() .
.
Якщо
![]() ,
то другий доданок в останньому виразі
можна розглядати як суму
,
то другий доданок в останньому виразі
можна розглядати як суму
![]() нескінченно
спадної геометричної прогресії
нескінченно
спадної геометричної прогресії
![]() з
першим членом
з
першим членом
![]() і знаменником
і знаменником![]() .
Тоді
.
Тоді
![]()
![]()
![]() .
.
Отриманий
ряд в силу однозначності розвинення і
є шуканим рядом Тейлора. Радіус збіжності
цього ряду визначається з умови
![]() .
Тоді
.
Тоді![]() .
Отже,
.
Отже,![]() .
.
Радіус
збіжності
![]() можна знайти інакше як відстань від
центра ряду
можна знайти інакше як відстань від
центра ряду
![]() до
найближчої особливої точки
до
найближчої особливої точки
![]() функції
функції
![]() (у
даної функції особлива точка єдина).
(у
даної функції особлива точка єдина).
