теория 1 курс / 3. Матрицы 1_исп

Раздел 3. Матрицы

3.1 Основные понятия

Матрицей называется прямоугольная таблица чисел, содержащая т строк одинаковой длины (или п столбцов одинаковой длины). Матрица записывается в виде:

или, сокращенно, , где (т.е.) – номер строки, (т.е. ) – номер столбца.

Матрицу А называют матрицей размера и пишут . Числа , составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего левого угла, образуют главную диагональ.

Пример 1. Элемент расположен в 1-й строке и 2-м столбце, а элемент находится в 3-й строке и 1-м столбце.

Пример 2. Матрица имеет размер , так как она содержит 2 строки и 4 столбца. Матрица 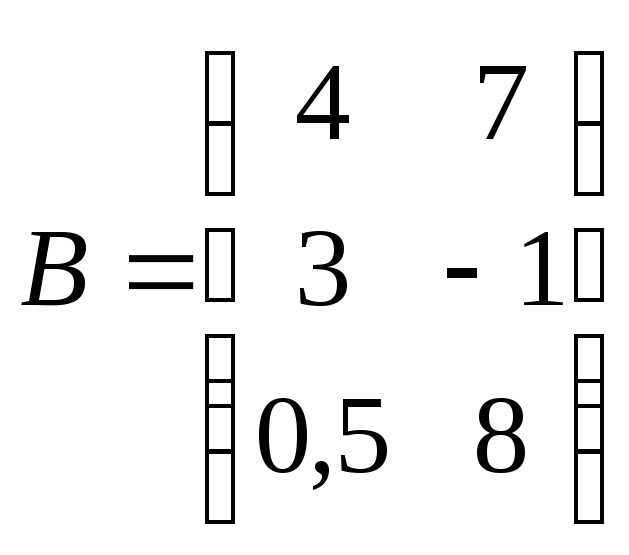имеет размер , так как она содержит 3 строки и 2 столбца.

Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т.е. , если , где , .

Матрица, у которой число сток равно числу столбцов, называется квадратной. Квадратную матрицу размера называют матрицей п-го порядка.

Пример 3. Матрицы и из примера 2 называются прямоугольными. Матрица – это квадратная матрица 3-го порядка. Она содержит 3 строки и 3 столбца.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.

Пример 4. – единичная матрица 3-го порядка.

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю. Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О.

В матричном исчислении матрицы О и Е играют роль 0 и 1 в арифметике.

Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:

, .

Матрица размера , состоящая из одного числа, отождествляется с этим числом, т.е. есть 5.

Матрица, полученная из данной, заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначается . Так, если , то если , то . Транспонированная матрица обладает следующим свойством: .

3.2 Операции над матрицами

Сложение

Операция сложения матриц вводится только для матриц одинаковых размеров.

Суммой двух матриц и называется матрица такая, что (, ).

Пример 5. .

Аналогично определяется разность матриц.

Умножение на число

Произведением матрицы на число k называется матрица такая, что b_ij=ka_ij (i=, j=).

Пример 6. , , .

Матрица называется противоположной матрице А.

Разность матриц можно определить так: .

Операции сложения матриц и умножение матрицы на число обладают следующими свойствами:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ,

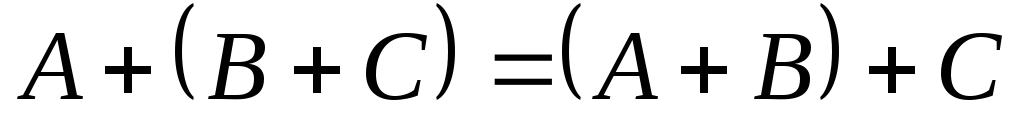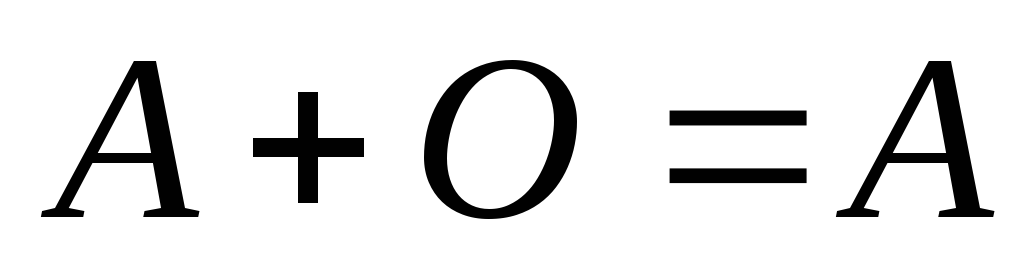где А, В, С – матрицы, α и β – числа.

Элементарные преобразования матриц

Элементарными преобразованиями матриц являются:

• перестановка местами двух параллельных рядов матрицы;

• умножение всех элементов ряда матрицы на число, отличное от нуля;

• прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А~В.

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например .

Пример 7. Привести к каноническому виду матрицу.

Решение: Выполняя элементарные преобразования, получаем

(поменяли местами I и III столбцы) ~ (I строку сложили со II строкой и результат записали во вторую строку; после этого I строку сложили с III строкой и результат записали в третью строку) ~ (I столбец умножили на (-3), сложили со II столбцом и результат записали во II столбец; затем I столбец умножили на (-2), сложили с III столбцом и результат записали в III столбец; после этого I столбец снова умножили на (-2) и сложили с IV столбцом, а результат записали в IV столбец) ~ (III столбец умножили на (-2), сложили со II столбцом и результат записали во II столбец; III столбец разделили на 2 и результат записали в III столбец; III столбец умножили на (-1), сложили с IV столбцом и результат записали в IV столбец) ~ (II строку умножили на 3, сложили с III строкой и результат записали в III строку) ~ (II столбец умножили на (-1), сложили последовательно с III и IV столбцами и результат записали соответственно в III и IV столбец) ~ . Получили матрицу канонического вида.

Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы А_т×п=(а_ij) на матрицу В_п×р=(b_jk) называется матрица С_т×р=(с_ik) такая, что

c_ik=a_i1∙b_1k+ a_i2∙b_2k+ ∙∙∙+ a_in∙b_nk , где i=, k=,

т.е. элемент i-ой строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А∙Е = Е∙А = А, где А – квадратная матрица, Е – единичная матрица того же размера.

Пример 4.

=.

x==

Матрицы А и В называются перестановочными (коммутирующими), если АВ=ВА.

Умножение матриц обладает следующими свойствами:

1. А∙(В∙С) = (А∙В)∙С;

2. А∙(В + С) = АВ + АС;

3. (А + В)∙С = АС + ВС;

4. α(АВ) = (αА)В,

если, конечно, написанные суммы и произведения матриц имеют смысл.

Для операции транспонирования верны свойства:

1. (А + В)^Т=А^Т + В^Т;

2. (АВ)^Т = В^Т∙А^Т.

Если задан многочлен , то матричным многочленом f(A) называется выражение вида , где для любого натурального п. Значением матричного многочлена f(A) при заданной матрице А является матрица.

Элемент строки назовем крайним, если он отличен от нуля, а все элементы этой строки, находящиеся левее его, равны нулю. Матрица называется ступенчатой, если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки.

Пример 5. В матрицах А и В отмечены крайние элементы каждой строки:

– не ступенчатая

– ступенчатая