23.25. Квантово-механическое описание систем. У.Ш. Рассчет числа возможных состояний ид.Газа.

Соотношение неопределенностей Гейзенберга ∆x∆p≥h устанавливает различия в описании состояния систем в квантовой и классической механике. Состояние частицы в классической механике описывается с помощью координат и импульсов (точка в фазовом -пространстве). Квантовая же частица в состоянии с определенными координатами (x, y, z) не обладает определенным импульсом. То есть, для квантовой частицы не существует состояний, в которые ее координаты и импульсы имели бы одновременно точные значения. Состояние квантовой системы описывает главная величина в квантовой механике – волновая функция  (x, y, z, t). Шредингер установил соответствующее уравнение для волновой функции. Его следует понимать как один из постулатов квантовой механики, и оно играет в ней такую же роль, как 2-ой закон Ньютона в классической механике. Для стационарных состояний, в которых вероятности измерения физических величин не зависят от времени, уравнение Шредингера имеет вид Для нахождения волновой функции должны быть еще заданы граничные условия, которые сводятся к требованию однозначности и непрерывности волновой функции и ее первой производной. Как и в любой теории, дающей вероятностное описание, в квантовой механике сопоставление с опытом производится для средних значений физических величин.

Рассмотрим общие свойства решений уравнения Шредингера на простом примере движения электрона в прямоугольной бесконечно глубокой потенциальной яме,

Видно, что уравнение Шредингера имеет решения, удовлетворяющие граничным условиям только при дискретных значениях квантовых чисел. n1, n2 и n3 образуют фазовое пр-во.

ЧИСЛО СОСТОЯНИЙ ОПРЕДЕЛЯЕТСЯ ФАЗОВЫМ ОБЪЕМОМ. ТОГДА ЭТА ЗАДАЧА СВОДИТСЯ К НАХОЖДЕНИЮ ФАЗОВОГО ОБЪЕМА ОБЛАСТИ E÷E+dE. Объем слоя dE=dV=4pi*R^2/8dR=4*pi(n1^2+n2^2+n3^2)

Значит

24.26. РАСПРЕДЕЛЕНИЯ В КВАНТОВОЙ СТАТИСТИКЕ. ЧАСТИЦА В ПРЯМОУГОЛЬНОМ ЯЩИКЕ. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР. МАТРИЦА ПЛОТНОСТИ.Квантовая статистика – это применение статистического метода Гиббса для описания квантовых систем. Суть статистического метода одинакова и для классических, и для квантовых систем: необходимо определить вероятность того, что система находится в данном микросостоянии. Для классической статистики микросостояние – это одновременное задание координат и импульсов (q, p) всех частиц системы. Для квантовой системы это невозможно из-за принципа неопределенности. Квантовая система может иметь только определенный набор дискретных значений энергий, называемый ее энергетическим спектром. Каждому значению энергии E_n соответствует одно или несколько различных квантовых состояний. Под n понимается совокупность квантовых чисел, которые и определяют состояние системы. Так что микросостояние квантовой системы – это задание полного набора квантовых чисел n (n₁, n₂, …) или соответствующих значений энергий E_n (E₁, E₂, …) системы. Пусть квантовая система находится в контакте с термостатом (окружающей средой) при температуре Т (заданы число частиц N, объем системы V и температура Т). Тогда, можно показать, что выражение для вероятности _n того, что система находится в квантовом состоянии с энергией E_n, определяется соотношением, подобным каноническое распределение Гиббса в квантовой статистике. Z называется статистической суммой системы Она заменяет в квантовой статистике статистический интеграл. Важно отметить, что_n – это именно вероятность данного состояния системы, а не вероятность системы иметь определенное значение энергии Е_n, потому что при вырождении данной энергии может соответствовать не одно, а несколько различных состояний. С помощью распределения Гиббса можно вычислить среднее по ансамблю (статистическое среднее) любой физической величины, зависящей от состояния системы. Если L (E_n) – значение этой величины для состояний с энергией E_n, то по определению среднего значения . Матрица плотности (оператор плотности)один из способов описания состояния квантовомеханической системы. В отличие от волновой функции, пригодной лишь для описания чистых состояний, оператор плотности в равной мере может задавать как чистые, так и смешанные состояния. Гармонический осциллятор в квантовой механике представляет собой квантовый аналог простого гармонического осциллятора, при этом рассматривают не силы, действующие на частицу, а гамильтониан, то есть полную энергию гармонического осциллятора, причём потенциальная энергия предполагается квадратично зависящей от координат. Гамильтониан квантового осциллятора массы m, собственная частота которого ω, выглядит так: Частица может двигаться по оси х в обоих направлениях, но не может находиться вне ящика, где U=∞, а ψ=0.. Уравнение Шредингера для одномерного движения внутри ящика Граничные условия:ψ(0)= ψ(α)=0. Общее решение ψ(x)=Asin(k*x)+Bcos(k*x) приВидно, что уравнение Шредингера имеет решения, удовлетворяющие граничным условиям только при дискретных значениях квантового числаn. Таким образом, энергия частицы в потенц. яме оказывается квантованной. Причем дискретность энергии возникла естественным образом, без каких-либо дополнительных предположений, как следствие граничных условий, налагаемых на волновую функцию. Оказывается, что состояние квантовой системы (электрон в потенциальной яме в нашем примере) определяется квантовым числом n.

27,28. РАСПРЕДЕЛЕНИЕ ФЕРМИ И БОЗЕ. Согласно квантовой теории все микрочастицы подразделяют на два класса, которым соответствуют две квантовые статисти­ки:1) частицы с полуцелым спином, их называют фермионами; они подчиняются статистике Ферми-Дирака; 2) частицы с целым спином — бозоны; они подчиняются статистике Бозе-Эйнштейна. Во всех трех статистиках (классической, Бозе-Эинштеина и Ферми-Дирака) допустимые микросостояния считаются равно­вероятными. Но различие их — в способах определения мик­росостояний и статистических весов. В статистике Больцмана считается, что даже тождественные частицы принципиально различимы. В квантовых же статистиках, наоборот, считается, что тождественные частицы принципиально неразличимы.

В статистике Ферми-Дирака в каждом квантовом состоянии может находиться не более одной частицы (принцип Паули), а в статистике Бозе-Эйнштейна — любое число частиц.

Для описания состояния системы частиц рассматривают во­ображаемое шестимерное пространство, каждая точка которого

характеризуется шестью координатами: х, у, z, p_x ,p_y ,p_z. Это так называемое фазовое пространство. Состояние системы определяется тем, как распределены в этом пространстве точ­ки, изображающие состояния всех N частиц системы. При этом нужно учесть присущий частицам корпускулярно-волновой ду­ализм, согласно которому неопределенности координаты х и со­ответствующей проекции импульса р_х могут быть определены только с неопределенностью, произведение которых, согласно принципу неопределенностей Гейзенберга, δxδp_x≥h . Аналогично и для других пар: у и p_y , z и р_г. Поэтому естественно считать, что данному состоянию части­цы в фазовом пространстве соответствует не точка, а фазовая ячейка, объем которой

Распределение частиц по таким фазовым ячейкам есть пре­дельно подробное квантовое описание состояния системы.

Квантовые распределения. Эти распределения представля­ют собой функции определяющие средние числа частицв одной фазовой ячейке с энергией или функции заполнения ячеек:

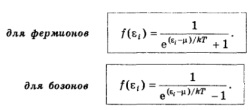
Здесь μ — так называемый химический потенциал (некоторая характерная энергия, значение которой можно найти из усло­вия нормировки: суммарное число частиц во всех фазовых ячейках должно быть равно полному числу N частиц макроси­стемы).