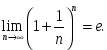мат.анализ
.rtf
Мат анализ
|
A)
D)
G)
|
|
C)
D)
G)
|
|
A)
B)
F)
|
|
A)
F)
ѓ
H)
|
|
орындалады: C) шегі 0-ге тең G) 1саны жоғарғы шекара H) 0 саны төменгі шекара |
|
A) шегі жоқ F) жоғарыдан шенелмеген G) ақырсыз үлкен емес
|
|
орындалады:
A)
E)
H)
|
|
D)
G)
H)
|
|
C)
D) жинақты G) фундаментальды тізбек
|
|
A) фундаментальды тізбек E) жинақты
H)
|
|
A)
C)
E)
|
|
B)
E)
F)
|
|
B)
D)
F)
|
|
A)
F)
G)
|
|
A)
E)
H)
|
|
B)
C)
G) |
|
B)
E)
G) |
|
мен теңдіктер:
B)
D)
F)
|
|
A)
E)
H)
|
|
B)
E)
F)
|
|
A)
B)
D)
|
|
B)
C)
D)
|
|
A) Лопиталь ережесін қолдана алмаймыз
D)
F)
|
|
B)
C)
D)
|
|
B)
C)
F)
|
|
A)
C)
H)
|
|
A)
B)
D)
|
|
A мен B жиындарының бірігуін көрсететін өрнек:
A)
C)
F)
|
|
A мен B жиындарының қиылысуын көрсететін өрнек:
A)
B)
H)
|
|
A мен B жиындарының симметриялық айырымын көрсететін өрнек:
A)
(B\A)
E)
H) B\ A. |
|
U жиынының ішкі жиындары A мен B –ның айырымын көрсететін өрнек:
D)
A\
(A
E)
F) |
|
U жиынының ішкі жиындары A мен B –ның бірігуін көрсететін өрнек:
B)
C)
H)
|
|
U жиынының ішкі жиындары A мен B –ның қиылысуын көрсететін өрнек:
C)
G)
H)
|
|
функциясының
алғашқы
A)
C)
E)
|
|
Бос жиынды көрсететін өрнек:
C)
D)
H)
|
|
Егер
A)
D)
H)
|
|
Егер
A)
D)
H)
|
|
Егер
D)
E)
F)
Анықталу аймағы
|
|
Егер
F)
G)
H)
|
|
Егер
A)
C)
H)
|
|
Егер
A)
C)
F)
|
|
Егер
B)
D)
F)
|
|
Егер
D)
E)
H)
|
|
Егер
B)
C)
F)
|
|
Егер
B)
E)
H)
|
|
Егер
E)
F)
H)
|
|
Егер
A)
B)
E)
|
|
Егер
E)
F)
H)
|
|
Егер
B)
D)
H)
|
|
Егер
C)
E)
ол
G)
|
|
Егер
B)
D)
оның
H)
оның
|
|
Егер
A)
C)
D)
ол
|
|
Егер
A)
C)
оның
D)
|
|
Егер
C)
E)
H)
ол
|
|
Егер
B)
E)
F)
ол
|
|
Егер
A)
C)
D)
|
|
Егер
B)
C) вертикаль асимптота жоқ
E)
(1;+ дөңестігі төмен қараған) |
|
Егер
C)
D)
F)
функция
|
|
Егер
A)
C)
H)
|
|
Егер
C)
E)
H)
|
|
Егер
A)
D)
G)
|
|
Егер
B) асимптотасы y=2, түзуі
C)
H)
оның ең кіші мәні
|
|
Егер
A)
оның
вертикаль асимптотасы
F)
оның
көлбеу асимптотасы
H)
|
|
Егер
A)
ол
B)
жоғары бағытталған)
H)
|
|
Егер
A) оның алғашқы функциясы бар
D)
F)
|
|
Егер
f
функциясы
C)
D)
F)
f
төменнен
шенелмеген жағдайда |
|
Егер
f
функциясы
B)
D)
G)
f
жоғарыдан
шенелмеген жағдайда |
|
Егер
M
саны
C)
E)
G)
|
|
Егер
m
саны
A)
E)
G)
|
|
Егер
A)
D)
G)
|
|
Егер
B)
оның
F)
G)
|
|
Егер В жиыны А жиынының ішкі жиыны болса, онда
A)
C)
F)
|
|
Егер
ѓ(x),
g(x),
h(x)
- функциялары
A)
D)
F)
|
|
Егер А) (u+х)ө=uө+хө
E)
G)
|
|
Егер
B)
E)
F)
|
|
Егер
B)
C)
H) Ол, бірінші немесе екінші текті үзіліс нүкте
|
|
Егер
B)
D)
G)
|
|
Егер
B)
E)
H)
|
|
Егер
A)
F)
G)
|
|
Егер C) осы кесіндіде оның ең үлкен мәні бар E) осы кесіндіде оның ең кіші мәні бар H) осы кесіндіде ол шенелген
|
|
Егер
C)
D)
H)
|
|
Егер
A)
D)
F)
|
|
Егер
А)
C)
G)
|
|
Егер
A)
E)
G)
|
|
Егер
C)
D)
F)
|
|
Егер
C)
E)
G)
|
|
Егер
A)
ол
D)
(-2;+ (дөңестігі төмен бағытталған) F) функцияның асимптотасы жоқ |
|
Егер
B)
G)
функция
H)
|
|
Егер
B)
E)
F) |
|
и алмастыруын қолдану жолдары
C)
E)
H)
|
|
A)
C)
E)
|
|
C)
D)
G)
|
|
B)
C)
F)
|
|
C) жинақты D) шенелген
E)
|

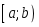 жиыны
үшін
орындалатын қатынас:
жиыны
үшін
орындалатын қатынас: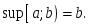
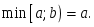
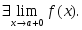
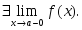
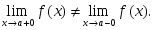
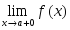 оң жақ шегі жоқ
оң жақ шегі жоқ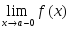 сол жақ шегі жоқ
сол жақ шегі жоқ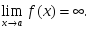
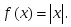
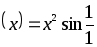
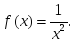
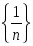 -
сандық тізбегіне қатысты келесі
пікірлер
-
сандық тізбегіне қатысты келесі
пікірлер
 -
сандық тізбегіне қатысты келесі
пікірлер
-
сандық тізбегіне қатысты келесі
пікірлер
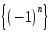 -
сандық тізбегіне қатысты келесі
пікірлер
-
сандық тізбегіне қатысты келесі
пікірлер
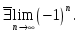
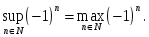
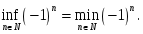
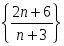 -
сандық
тізбегіне қатысты келесі пікірлер
орындалады:
-
сандық
тізбегіне қатысты келесі пікірлер
орындалады: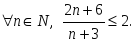
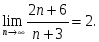
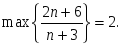
 -
сандық
тізбегіне қатысты келесі пікірлер
орындалады:
-
сандық
тізбегіне қатысты келесі пікірлер
орындалады: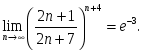
 -
сандық
тізбегіне қатысты келесі пікірлер
орындалады:
-
сандық
тізбегіне қатысты келесі пікірлер
орындалады: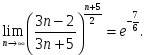
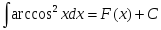 теңдігі
дұрыс болатындай F(x):
теңдігі
дұрыс болатындай F(x):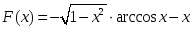
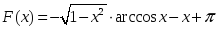
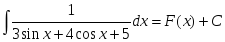 теңдігі
дұрыс болатындай F(x):
теңдігі
дұрыс болатындай F(x):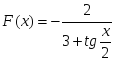
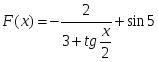
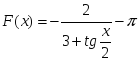
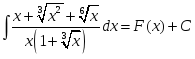 теңдігі
дұрыс болатындай F(x):
теңдігі
дұрыс болатындай F(x):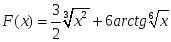
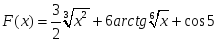
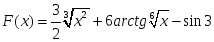

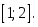
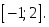
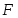 функциясы
берілген
функциясы
берілген
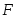 функциясы
функциясы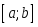 кесіндісінде
үзіліссіз болуы қажет
кесіндісінде
үзіліссіз болуы қажет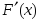 туындысы
бар болуы қажет
туындысы
бар болуы қажет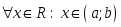 нүктелерінде
нүктелерінде
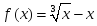 функциясы
үшін Ролль теоремасының шарты
орындалатын аралықтар:
функциясы
үшін Ролль теоремасының шарты
орындалатын аралықтар: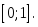
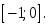
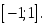
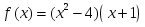 функциясы
үшін:
функциясы
үшін: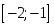 кесіндіде
Ролль теоремасының шарты орындалады
кесіндіде
Ролль теоремасының шарты орындалады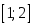 кесіндіде Лагранж теоремасының шарты
орындалады
кесіндіде Лагранж теоремасының шарты
орындалады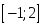 кесіндіде Ролль теоремасының шарты
орындалады
кесіндіде Ролль теоремасының шарты
орындалады функциясына
байланысты қасиеттер
функциясына
байланысты қасиеттер
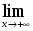
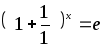
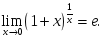

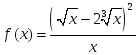 функциясының
алғашқы функциясы:
функциясының
алғашқы функциясы: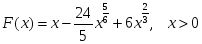 -
-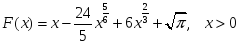
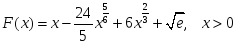
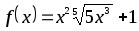 функциясының
алғашқы функциясы:
функциясының
алғашқы функциясы: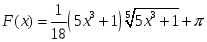


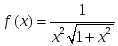 функциясының
алғашқы функциясы:
функциясының
алғашқы функциясы: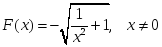
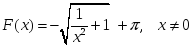
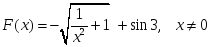
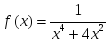 функциясының
алғашқы функциясы:
функциясының
алғашқы функциясы: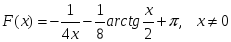
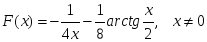

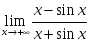 шегіне
қатысты
дұрыс
тұжырымдар:
шегіне
қатысты
дұрыс
тұжырымдар: шегі жоқ
шегі жоқ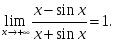
 шегіне
қатысты
орындалатын
тұжырым:
шегіне
қатысты
орындалатын
тұжырым: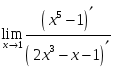 шегі бар
шегі бар
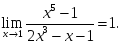
 шегіне
қатысты
орындалатын
тұжырымдар:
шегіне
қатысты
орындалатын
тұжырымдар: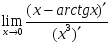 шегі бар
шегі бар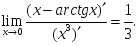
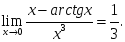
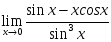 шегіне
қатысты
орындалатын
тұжырымдар:
шегіне
қатысты
орындалатын
тұжырымдар: шегі бар
шегі бар
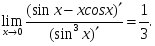
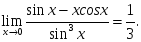
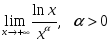 шегіне
қатысты
орындалатын
тұжырымдар:
шегіне
қатысты
орындалатын
тұжырымдар: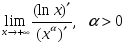 шегі жоқ.
шегі жоқ.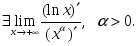
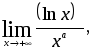
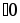
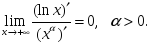
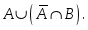

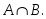
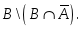
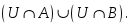
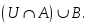
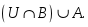
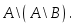
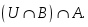
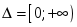 аралығында
берілген
аралығында
берілген
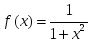
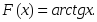
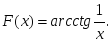
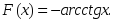
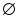
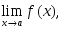
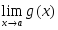 шектері бар және олар ақырлы
болса,
онда::
шектері бар және олар ақырлы
болса,
онда::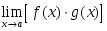 шегі де бар
шегі де бар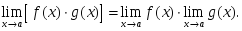
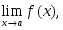
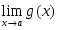 шектері бар және олар ақырлы болса,
онда::
шектері бар және олар ақырлы болса,
онда::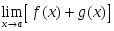 шегі де бар
шегі де бар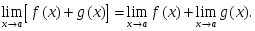
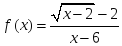 берілсе, онда:
берілсе, онда: нүктесінде
нүктесінде анықталмаған
анықталмаған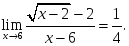
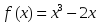 берілсе, онда:
берілсе, онда: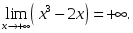
 тақ
функция
тақ
функция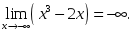
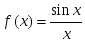 берілсе, онда:
берілсе, онда: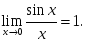
 жұп
функция.
жұп
функция.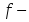 функциясы
функциясы
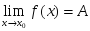 берілсе, онда:
берілсе, онда: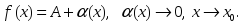
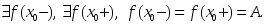
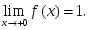
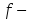 тақ функция
тақ функция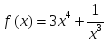 берілсе, онда:
берілсе, онда: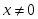 нүктелерінде функция үзіліссіз
нүктелерінде функция үзіліссіз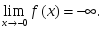
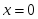 - функцияның 2 - текті үзіліс нүктесі
- функцияның 2 - текті үзіліс нүктесі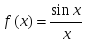 берілсе, онда:
берілсе, онда: - үзіліссіз функция
- үзіліссіз функция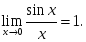
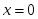 - функцияның жойылатын үзіліс нүктесі
- функцияның жойылатын үзіліс нүктесі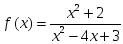 берілсе, онда:
берілсе, онда: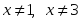 нүктелерде функция үзіліссіз
нүктелерде функция үзіліссіз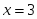 - функцияның 2 - текті үзіліс нүктесі
- функцияның 2 - текті үзіліс нүктесі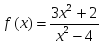 берілсе, онда:
берілсе, онда: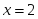 - функцияның 2 - текті үзіліс нүктесі
- функцияның 2 - текті үзіліс нүктесі жұп
функция
жұп
функция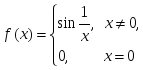 берілсе, онда:
берілсе, онда: - функцияның 2-текті үзіліс нүктесі
- функцияның 2-текті үзіліс нүктесі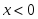 нүктелерінде функция үзіліссіз
нүктелерінде функция үзіліссіз нүктелерінде функция үзіліссіз
нүктелерінде функция үзіліссіз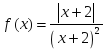 берілсе, онда:
берілсе, онда: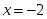 нүктеде функция анықталмаған
нүктеде функция анықталмаған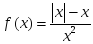 берілсе, онда:
берілсе, онда: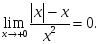
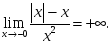
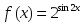 берілсе, онда:
берілсе, онда: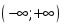 аралығында үзіліссіз
аралығында үзіліссіз
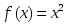 берілсе, онда:
берілсе, онда: нүктедегі жанамасы
нүктедегі жанамасы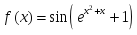 берілсе, онда:
берілсе, онда: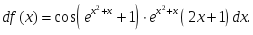
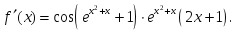
 аралығында үзіліссіз
аралығында үзіліссіз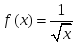 берілсе, онда:
берілсе, онда: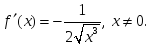
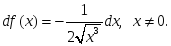
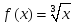 берілсе, онда:
берілсе, онда: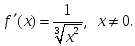
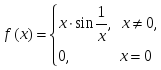 берілсе, онда:
берілсе, онда: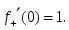
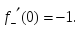
 тақ
функция
тақ
функция аралығында
фунция өседі
аралығында
фунция өседі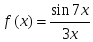 берілсе, онда::
берілсе, онда::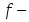 жұп
функция
жұп
функция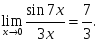
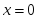 нүктеде анықталмаған
нүктеде анықталмаған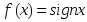 берілсе, онда::
берілсе, онда::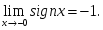
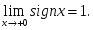
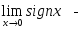 шегі жоқ
шегі жоқ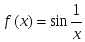 берілсе, онда::
берілсе, онда::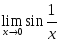 шегі жоқ
шегі жоқ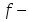 тақ
функция
тақ
функция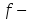 шенелген функция
шенелген функция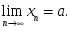
 -шенелген
тізбек
-шенелген
тізбек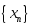 -
фундаментальды тізбек
-
фундаментальды тізбек функциясы
берілсе, онда:
функциясы
берілсе, онда: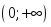 аралығында
өседі
аралығында
өседі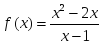 функциясы
берілсе, онда:
функциясы
берілсе, онда: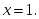
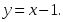
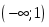 аралығында
ол өседі
аралығында
ол өседі
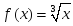 функциясы
берілсе, онда:
функциясы
берілсе, онда: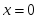 нүктесінде өседі
нүктесінде өседі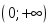 аралығында ол дөңес (график дөңестігі
аралығында ол дөңес (график дөңестігі
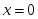 - оның иілу нүктесі
- оның иілу нүктесі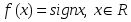 функциясы берілсе, онда:
функциясы берілсе, онда: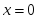 - оның үзіліс нүктесі
- оның үзіліс нүктесі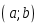 аралығында
кемімелі болса, онда:
аралығында
кемімелі болса, онда: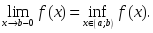
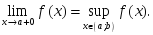

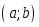 аралығында
өспелі болса, онда:
аралығында
өспелі болса, онда: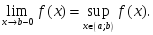
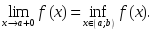
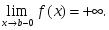
 сандық
тізбектің жоғарғы шегі болса, онда:
сандық
тізбектің жоғарғы шегі болса, онда: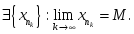
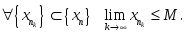

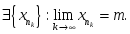
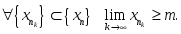

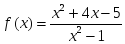 берілсе, онда:
берілсе, онда: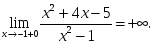
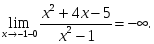
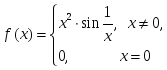 берілсе, онда:
берілсе, онда: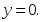
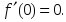
 аралығында
дифференциалданады
аралығында
дифференциалданады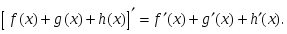

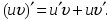
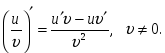
 және
және
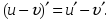
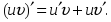

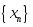 сандық
тізбектің шегі а
болса, онда:
сандық
тізбектің шегі а
болса, онда: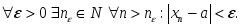

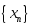 -
фундаментальды тізбек
-
фундаментальды тізбек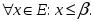
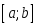 кесіндісінде үзіліссіз болса, онда:
кесіндісінде үзіліссіз болса, онда: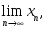
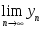 шектері
бар болса, онда:
шектері
бар болса, онда: шегі
бар
шегі
бар -шенелген
тізбек
-шенелген
тізбек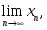
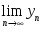 шектері
бар болса, онда:
шектері
бар болса, онда: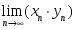 шегі
бар
шегі
бар -шенелген
тізбек
-шенелген
тізбек
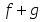 функциясы
функциясы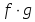 функциясы
функциясы
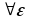
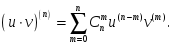
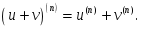
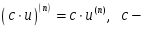 тұрақты
тұрақты
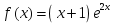 функциясы
берілсе, онда:
функциясы
берілсе, онда: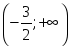 аралығында өседі
аралығында өседі аралығында,
ал
аралығында,
ал
 нүктесінде
дифференциалданса, онда:
нүктесінде
дифференциалданса, онда:
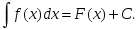
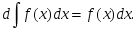
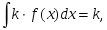
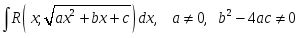 нтегралына
Эйлер
нтегралына
Эйлер
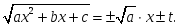
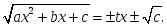
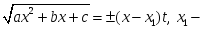 квадрат үшмүшеліктің нақты түбірі
квадрат үшмүшеліктің нақты түбірі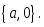
 мен
мен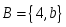 жиындарының
қиылысуын көрсететін өрнек:
жиындарының
қиылысуын көрсететін өрнек: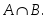

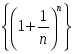 сандық
тізбегі үшін келесі пікірлер орындалады:
сандық
тізбегі үшін келесі пікірлер орындалады: