
Методичка по сопромату (I семестр)
.pdf
70
J z = 201233 + 20 3 3.32 + 2 12163 + 2 16 6.22 = 2611 см4.
Відстань від нейтральної лінії до найбільш віддаленого розтягнутого волокна h1=4.8 см, а до стиснутого - h2=14.2 см. При цьому осьові моменти опору перерізу для крайніх розтягнутих та стиснутих волокон будуть дорівнювати
W = |
J z |
|
= 2611 = 544 см3 |
, W = |
J z |
= 2611 =183.9 см3. |
|
|
|||||
1 |
h1 |
4.8 |
2 |
h2 |
14.2 |
|
|
|
|||||
Далі за |
формулою |
(3.6) |
|
обчислюємо найбільші |
||
розтягуючі та стискаючі напруження
σmax = |
|
M max |
= |
|
21.33 103 |
|
= 39.2 10 |
6 |
Н |
= 39.2 МПа <[σ+ ], |
|
|
W1 |
|
544 10−6 |
|
м2 |
||||||
σmin = |
M max |
|
= |
|
21.33 103 |
=116 10 |
6 |
Н |
=116 МПа. >[σ− ]. |
||
|
W2 |
183.9 10−6 |
|
м2 |
|||||||
|
|
|
|
|
|
||||||
Перенапруження за стискаючими напруженнями складає
ε = 6110100 = 5.45% > 5%, що недопустимо.
Перевірку міцності балки за дотичними напруженнями виконаємо за першою формулою (3.13) в небезпечному перерізі над лівою опорою, де діє Qmax=32 кН. Обчислюємо
|
|
|
|
|
Sz =14.2 |
2 7.1 = 201.6 |
см3, |
|
|
|
|
Q |
S |
z |
|
32 103 201.6 |
10−6 |
|
106 |
Н |
|
τmax = |
max |
|
= |
|
|
=12.35 |
|
=12.35 МПа <[τ]. |
||
d J z |
|
20 10−3 2611 10−8 |
м2 |
|||||||
|
|
|
|
|
|
|||||
Отже, міцність за дотичними напруженнями забезпечена. Приклад 3.6. Для дерев’яної балки (рис. 3.6) визначити
розміри круглого (d) та прямокутного (h і b) поперечних

71
перерізів і побудувати епюри нормальних і дотичних напружень, якщо [σ]=10 МПа, [τ]=2 МПа, K=h/b=2.4.
Розв’язання виконуємо у такому порядку.
1. Визначити опорні реакції та побудувати епюри Q і M.
∑M A =q 3 1.5 − M + F 5 −VB 4 = 0
VB = 14 (20 3 1.5 − 40 + 20 5) = 1504 = 37.5 кН,
∑M B =F 1+VA 4 − q 3 2.5 − M = 0
VA = 14 (−20 1+ 20 3 2.5 + 40) = 1704 = 42.5 кН.
Перевірка: ∑Y =VA +VB − q 3 − F = 42.5 +37.5 − 20 3 − 20 = 80 −80 = 0.
Отже, реакції визначені правильно.
Для побудови епюр Q і M виділимо на балці три ділянки І, ІІ і ІІІ (рис.3.6).
Ділянка І (0 ≤ х ≤ 3 м)
Q(x) =VA − qx - л.ф.; Q x=0 = 42.5 кН, Q x=3м = 42.5 − 20 3 = −17.5кН.
Так як Q змінює знак на ділянці, знаходимо точку екстремуму функції М
|
Q(x) =VA − qx0 |
= 0 x0 =VA q = 42.5 / 20 = 2.13 м. |
|||||||||
|
|
|
|
|
M (x) =VAx −qx2 2 - парабола; |
||||||
|
M |
x=0 |
= 0, |
M |
x=3м |
= 42.5 3 − 20 32 2 = 37.5 кНм, |
|||||
|
|
|
|
|
|
|
|
|
|||
M |
max |
= M |
x=x0 =2.13 |
м |
= 42.5 2.13 − 20 2.132 2 = 45.16 кНм. |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Ділянка ІІ (0 ≤ х ≤ 1 м) |
|||||
Q(x) = −VB + F = −37.5 |
+ 20 = −17.5 кН = const; M(x) =VB x − F(1+ x) − л.ф.; |
||||||||||
|
M |
|
x=0 = −20 кНм; M |
|
x=1 м = 37.5 1−20 2 = −2.5 кНм. |
||||||
|
|
|
|||||||||
|
|
|
|||||||||
Ділянка ІІІ (0 ≤ х ≤ 1 м)
72
Q(x) = F = 20 кН = const; M (x) = −Fx − л.ф.;
M x=0 = 0 кНм; M x=1 м = −20 1 = −20 кНм.
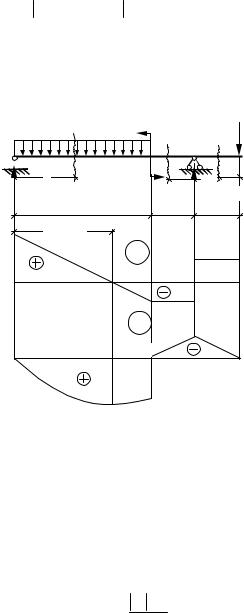
За обчисленими значеннями Q і M на рис. 3.6 побудовані епюри поперечних сил та згинальних моментів, з яких знаходимо: Qmax =42.5 кН; Mmax =42.16 кНм.
q=20кН/м I
 A x
A x
VА=42.5кН
3м x0=2.13м
42.5
M=40кНм |
F=20кН |
|
|
II |
III |
|
|
|
B |
|
|
x |
x |
|
|
|
VB=37.5кН |
|
|
1м |
1м |
|
Q |
кН |
|
|
|
|
20 |
|
|
|
17.5 |
45.16 |
M |
кНм |
20 |
2.5 |
|
||
|
|
37.5 |
|
Рис. 3.6
2. Виконати розрахунок на міцність балки круглого поперечного перерізу.
Запишемо умову міцності балки за нормальними напруженнями
M
W ≥ [σmax] ,
73
але для круглого поперечного перерізу W =πd 3 32 , тому
32 , тому
|
|
|
|
|
|
|
|
πd 3 |
≥ |
|
M |
|
max |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
[σ] |
|
|
|
|
|
||||
звідки знаходимо d ≥ |
3 32 M max |
= 3 32 45.16 103 |
= 0.3584 м. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
π[σ] |
|
|
|
|
3.14 10 106 |
|
|
||||
|
Приймаємо |
|
d=36 см. |
|
|
|
При |
цьому |
|||||||||||
W = |
3.14 0.353 |
= 4.21 10−3 м3 , а |
|
|
|
|
|
|
|
|
|
|
|
||||||
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σmax = |
|
M |
|
max |
= |
45.16 103 |
= 9.86 10 |
6 |
Н |
= 9.86 МПа <[σ] |
|
|||||||
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
W |
4.58 10−3 |
|
м2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
на ε = 0.14 100 =1.4% < 5%, що дозволяється.
10
З формули (3.1) видно, що нормальні напруження розподіляються за висотою перерізу лінійно.
σy=0 = 0 - на нейтральній лінії,
σmax = ±9.86 МПа - в крайніх волокнах балки.
min
За цими значеннями на рис. 3.7, а побудовано епюру нормальних напружень у небезпечному перерізі балки.
Перевіримо умову міцності балки за дотичними напруженнями
τmax = |
4 |
|
|
Q |
max |
= |
4 42.5 103 |
4 |
= 0.56 106 |
Н |
= 0.56 |
МПа <[τ]. |
||
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
A |
3 |
3.14 |
0.362 |
м2 |
||||||
|
|
|
|
|
|
|
|
|||||||
Отже, міцність балки за дотичними напруженнями також забезпечена.

74
В довільній точці круглого поперечного перерізу, яка лежить на відстані y від нейтральної лінії, дотичні напруження визначаються за формулою
|
4 |
|
|
Q |
|
|
|
y2 |
|
|
τ = |
|
|
|
|
max |
1 |
− |
|
|
. |
|
|
|
|
|
|
2 |
||||
|
3 |
|
|
|
A |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|||
Функція τ=f(y) – парабола, тому для побудови її графіка обчислюємо три значення τ y=0 =τmax = 0.56 МПа, τ y=±r = 0 .
Відповідно до цих значень на рис. 3.7, б побудована епюра дотичних напружень в небезпечному перерізі балки.
3. Виконати розрахунок на міцність балки прямокутного поперечного перерізу.
Осьовий момент опору прямокутного поперечного
перерізу визначається |
за |
формулою |
W = |
bh2 |
. Якщо відоме |
|||||||||||||||
6 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
співвідношення |
|
h |
|
= K , |
то |
|
b = |
|
h |
і умова |
міцності |
балки за |
||||||||
|
b |
|
K |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нормальними напруженнями набуває вигляду |
|
|
|
|||||||||||||||||
|
|
|
|
|
W = |
|
h3 |
|
≥ |
|
M |
|
max |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
6K |
|
[σ] |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
звідки знаходимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
h ≥ 3 6K M max |
= 3 |
6 2.4 45.16 103 |
= 0.403 м і |
b = |
|
0.403 |
= |
0.168 м. |
||||||||||||
|
10 106 |
|
|
|
|
2.4 |
||||||||||||||
[σ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Приймаємо h=40 см, b=17 см. При таких розмірах поперечного перерізу

75
|
|
|
|
|
W = |
bh2 |
= |
0.17 0.42 |
= 4.53 10−3 м3 , |
||||||
|
|
|
|
|
6 |
|
|||||||||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
||
σmax = |
|
M |
|
max |
= |
|
45.16 103 |
= 9.97 10 |
6 |
Н |
= 9.97 МПа <[σ] |
||||
|
|
|
|||||||||||||
|
|
|
|||||||||||||
|
W |
|
|
4.53 10−3 |
|
м2 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
на ε = 0.03 100 = 0.3% < 5%, що дозволяється.
10
По висоті балки нормальні напруження змінюються лінійно. В крайніх волокнах, що найбільш віддалені від нейтральної лінії, вони мають найбільше значення
σmax = ±9.97 МПа,
min
ана нейтральній лінії – дорівнюють нулю. Епюра нормальних напружень зображена на рис. 3.8, а.
Перевіримо міцність балки за дотичними напруженнями
τmax = |
3 |
|
|
Q |
max |
= |
3 42.5 103 |
= 0.94 106 |
Н |
= 0.94 МПа <[τ] , |
|
|
|
|
|
|
|||||
2 |
|
|
|
|
2 0.4 0.17 |
м2 |
||||
|
|
|
|
A |
|
|
||||
тобто міцність балки за дотичними напруженнями забезпечена. Для побудови епюри дотичних напружень використаємо
формулу (3.9)
|
3 |
|
Q |
|
|
|
4y2 |
|
, |
|
|
|
|
|
|||||||
τ = |
|
|
|
max |
1 |
− |
|
|
|
|
|
|
|
|
|
2 |
|||||
|
2 |
|
|
A |
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|||
з якої витікає, що функція τ=f(y) – парабола.
τ y =±r = 0, а τmax =τ y =0 = 32 QAmax = 0.94 МПа.
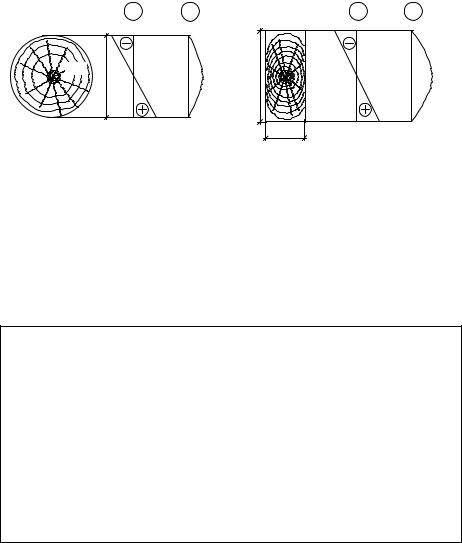
За цими значеннями на рис. 3.8, б побудовано епюру дотичних напружень у небезпечному перерізі балки.
 н.л.
н.л.
76
а |
б |
а |
б |
σ МП |
τ МП |
σ МП |
τ МП |
|
9.86 |
|
|
9.97 |
|
|
|
|
|
м |
|
|
н.л. |
|
d=36с |
|
0.56 |
0.94 |
|
|
|
|||
|
h=40мс |
|
|
|
|
9.86 |
b=17с |
|
9.97 |
|
|
|
Рис. 3.7 |
Рис. 3.8 |
4. Виконати контроль обчислень на ПЕОМ згідно з інструкцією до програми ”PROCH” (див. додаток 5). Усі необхідні для вводу в ПЕОМ дані наведені нижче
Робота №3 з опору матеріалів (задача 1)
Іванов І.І., гр.M-21, |
|
|
||||
сх.-вар., par |
|
|
1 7 0 |
|
||
Число ділянок |
|
3 |
|
|||
Номери опорних точок |
1 3 |
|
||||
Співвідношення розмірів перерізу |
2.4 |
|||||
----------------------------------------- |
|
|||||
№ т.| Xi[м] |
Mi[кнм] Fi[кн] qi[кн/м] |
|
||||
----------------------------------------- |
|
|||||
1 |
| |
0.00 |
0.00 |
0.00 |
-20.00 |
|
2 |
| |
3.00 -40.00 |
0.00 |
0.00 |
|
|
3 |
| |
4.00 |
0.00 |
0.00 |
0.00 |
|
4 |
| |
5.00 |
0.00 |
-20.00 |
0.00 |
|
Контрольні дані |
h, b, d |
0.402 0.168 0.358 |
||||
Максимальні зусилля |M|max, |Q|max |
45.16 42.50 |
|||||
77
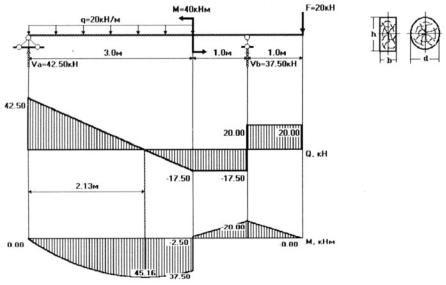
Результати обчислень на ПЕОМ за програмою ”PROCH”, що виконані згідно з інструкцією (див. додаток 5), наведені на рис.3.9.
78
Задача 1. Розрахунок дерев’яної балки. h/b=2.4
Результати розрахунку
Опорні реакції Va=42.50кН Vb=37.50кН
|M|max=45.16кНм при Х=2.13м |Q|max=42.50кН при Х=0.00м
Розміри прямокутного і круглого перерізів h=0.402м b=0.168м d=0.358м
Максимальні напруження для прямокутного і круглого перерізів
Smax_pr=10.009МПа Tmax_pr= 0.947МПа
Smax_cr=10.025МПа Tmax_cr= 0.563МПа
Виконав на ПЕОМ ст. Іванов І.І., гр.M-21, сх.-вар. 1 7
Рис. 3.9
79
Дерев’яну балку, показану на рис. 3.6, розрахувати методом граничного стану. Розрахункові опори деревини згинанню R=15МПа, сколюванню Rск=2.2МПа, коефіцієнт надійності за навантаженням n=1.1, коефіцієнт умов роботи балки m=0.8, h/b=2.
1. З епюр Q і M знаходимо: Qmax =42.5 кН; Mmax
=42.16 кНм.
2. Виконати розрахунок на міцність балки круглого поперечного перерізу.
Запишемо умову міцності за нормальними напруженнями
σmax = M max n ≤ mR.
W
Виходячи з умови міцності, маємо
|
|
|
|
|
|
|
|
|
|
W ≥ |
|
|
M |
|
max n |
, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mR |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
але для круглого поперечного перерізу |
|
W = |
πd 3 |
, тому |
|
|
|||||||||||||||||||||||
|
|
32 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
πd 3 |
|
≥ |
|
M |
|
max n |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
mR |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
звідки знаходимо |
d |
32 M max n |
|
= 3 |
32 45.16 10 |
3 1.1 |
= 0.3485 м. |
|
|||||||||||||||||||||
≥ 3 |
|
|
|
|
3.14 |
0.8 15 106 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
πmR |
|
|
|
|
|
|
|
|
|
|||||||||||
|
Приймаємо |
d=35 см. |
|
|
|
|
|
При |
цьому |
||||||||||||||||||||
W = |
3.14 0.353 |
= 4.58 10−3 м3 , а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
σmax = |
|
|
M |
|
max n |
= |
45.16 103 |
1.1 |
=11.8 10 |
6 |
|
Н |
=11.8 МПа < mR =12МПа |
||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
W |
4.21 10 |
−3 |
|
|
|
м2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
