
Методичка по сопромату (I семестр)
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
110 |
τmax = |
|
Q |
|
max n Sz |
= |
107.5 103 |
708 10−6 |
= 30.5 10 |
6 |
Н |
= 30.5МПа < mRзс. |
||
|
|
||||||||||||
|
|
||||||||||||
|
|
|
d J z |
|
9 |
10−3 27696 10−8 |
|
м2 |
|||||
|
|
|
|
|
|
|
|
||||||
Тобто, умова міцності балки за дотичними напруженнями виконується.
4. Перевірити балку на міцність за головними напруженнями за IV теорією міцності.
З епюр Q і M видно (рис. 3.20, б ,в), що небезпечним перерізом балки за головними напруженнями може бути тільки переріз D, де діють M=257.5 кНм та Qmax =92.5 кН.
Побудуємо епюри нормальних σ та дотичних τ напружень в цьому перерізі. Для цього обчислимо нормальні і дотичні напруження в характерних точках перерізу (рис. 3.21, а).
Так як σ = |
M y |
= f ( y) - лінійна функція, то для побудови |
|||||||||||||||||||||
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
J z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
її графіка достатньо знати два значення |
|
|
|
|
|
|
|
|
|
||||||||||||||
σ(1) |
=σ |
|
y=h / 2 |
=σmax = |
|
M |
= |
257.5 103 |
= 209.2 10 |
6 |
Н |
|
= 209.2 МПа, |
|
|||||||||
|
|
|
|||||||||||||||||||||
|
Wz |
1231 10−6 |
|
м2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
σ(2) = |
σ |
|
y=h / 2−t |
= |
M (h / 2 |
−t) |
= |
257.5 103 (0.45 / 2 −0.0142) |
=196 |
10 |
6 Н |
= |
|||||||||||
|
|||||||||||||||||||||||
|
|
J z |
|
|
27696 10−6 |
|
|
|
|
|
м2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
=196 МПа,
σ(4) =σ y=0 = 0 - на нейтральній лінії.
У верхній частині поперечного перерізу (рис. 3.21, а) діють такі ж самі стискаючі напруження, так як М>0. Епюру напружень σ побудовано на рис. 3.21, б.
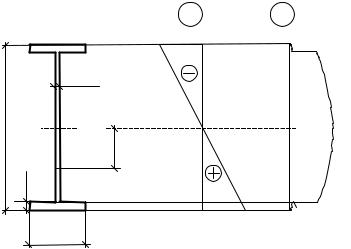
а
h=450
111
|
1’ |
б |
σ МПа в |
τ МПа |
|
|
|
|
|
|
2’ |
|
|
|
|
d=9 |
|
|
|
|
3’ |
|
|
|
|
4 |
н.л. |
|
26.3 |
t=14,2 |
2 |
-t)/2 |
196 |
|
(h/2 |
|
|||
|
3 |
|
|
25.8 |
|
|
|
|
18.4 |
|
1 |
|
209.2 |
1.03 |
b=160
Рис. 3.21
Дотичні напруження в характерних точках поперечного перерізу обчислюємо за формулою Журавського
|
|
|
|
|
|
|
|
|
|
|
|
|
τ = |
Q Sz ( y) |
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b J z |
|
|
|
|
|
|
|
|
|
Sz(1) |
= 0; Sz(2) |
= |
bt |
(h −t) = |
0.16 0.0142 |
(0.45 −0.0142) = 4.95 10−4 м3; |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
Sz(3) |
= |
bh |
(h −t) + |
3 |
d(h |
/ 2 −t)2 |
= 4.95 10 |
−4 + |
3 |
0.009(0.45 / 2 −0.0142)2 = |
||||||||||||||
|
|
|
||||||||||||||||||||||
|
2 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
||||
|
|
|
|
|
= 6.45 10−4 м3; |
Sz(4) = Sz |
|
= 7.08 10−4 м3. |
|
|||||||||||||||
|
|
|
п |
Q Sz (2) |
|
|
92.5 103 4.95 10−4 |
|
|
|
6 Н |
=1.03 МПа; |
||||||||||||
τ1 = |
0; τ |
2 = |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
=1.03 10 |
|
|
||||
|
b J z |
|
0.16 |
27696 10−8 |
|
м2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
112
c |
= |
|
Q Sz (2) |
= |
|
92.5 103 |
4.95 10−4 |
=18.37 |
10 |
6 |
|
Н |
|
=18.37 МПа; |
||||
τ2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
d J z |
|
0.009 27696 10−8 |
|
|
|
м2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
τ3 |
= |
Q Sz (3) |
= |
92.5 103 |
6.95 10−4 |
|
= 25.79 |
10 |
6 |
|
Н |
|
= 25.79 МПа; |
|||||
|
d J z |
|
0.009 27696 10−8 |
|
|
м2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
τ4 |
= |
|
Q Sz (4) |
|
= |
|
92.5 103 |
7.08 10−4 |
|
= 26.27 10 |
6 |
|
Н |
|
= 26.27 МПа |
|||
|
d J z |
|
|
0.009 27696 10−8 |
|
|
|
м2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
За обчисленими значеннями τ на рис. 3.21, в побудовано епюру дотичних напружень.
З епюр σ і τ (рис. 3.21, б, в) видно, що небезпечною точкою поперечного перерізу при перевірці міцності за головними напруженнями є точка переходу від полиці до стінки
2(2′), де діють напруження σ=196 МПа і τ=18.37 МПа. В цій точці обчислимо еквівалентне напруження за IV теорією міцності (3.16).
σекв =  σ 2 +3τ 2 =
σ 2 +3τ 2 =  1962 +3 18.372 =198.6 МПа < mRзг = 215 МПа.
1962 +3 18.372 =198.6 МПа < mRзг = 215 МПа.
Тобто, двотавр №45 задовольняє усім умовам міцності за нормальними, дотичними і головними напруженнями.
5. Визначити методом початкових параметрів прогини і кути повороту на межах усіх ділянок балки.
Приймаємо початок координат в крайній лівій точці балки і позначимо ділянки (рис. 3.20, г). При такому початку координат рівномірно розподілене навантаження q1 не задовольняє умові безперервності. Тому продовжуємо її до
113
кінця балки і прикладаємо додатне навантаження, що компенсує q1 і починає діяти в точці D (рис. 3.20, г).
Запишемо універсальне рівняння пружної лінії балки для прогинів на усіх ділянках
|
|
EJy = EJy0 + EJθ0 x− |
M (x −0)2 |
|
|
+ |
|
VA (x −2.5)3 |
|
|
+ |
q1(x −2.5)4 |
|
|
|
− |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
4! |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
← |
|
I |
|
|
|
|
|
|
|
|
← |
|
II |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0≤x≤2.5м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5м≤x≤7.5м |
|
|
|
|
|
|
|
|||||||||
|
|
− F(x −7.5)3 + q1(x −7.5)4 |
|
+VB (x −10.5)3 |
− |
|
|
q2 (x −10.5)4 |
|
|
|
|
|
. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
4! |
|
|
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
4! |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
← |
|
III |
|
|
|
|
← |
|
IV |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
7.5м≤x≤10.5м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10.5м≤x≤12.5м |
|
|
|
|
|
|
|
|||||||||||||
|
|
Невідомі початкові параметри EJy0 і EJθ0 визначимо з |
||||||||||||||||||||||||||||||||||||||||||||
умов закріплення балки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
EJy |
|
= EJy |
|
|
|
|
= EJy |
|
+ EJθ |
|
2.5 − |
30 |
2.5 |
2 |
= |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
A |
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
I |
x=2.5 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
10.52 |
|
|
107.5 103 |
20 8 |
4 |
|
100 33 |
|
|
|
|
20 34 |
|
||||||||||||||
EJyB |
= EJyIII |
|
|
= EJy0 + EJθ0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
10.5 − |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
− |
|
|
|
|
|
− |
|
|
+ |
|
|
|
= 0. |
|||||||||||||||||
|
|
|
|
|
|
x=10.5м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
6 |
|
|
24 |
|
|
6 |
|
|
|
|
|
|
24 |
|
|||||
|
|
Після обчислень одержимо таку систему рівнянь для визначення |
||||||||||||||||||||||||||||||||||||||||||||
початкових параметрів: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
EJyA = EJy0 + 2.5EJθ0 −93.75 = 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
EJy |
B |
= EJy +10.5EJθ |
0 |
+3723.75 = |
0 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
З розв'язування системи рівнянь отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
EJy0 =1286.64 кНм3; EJθ0 = −477.16 кНм2 , де |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
EJ = 2 105 106 27696 10−8 = 5.5392 107 Н м2 - |
|
|
|
|
жорсткість |
|
при |
|||||||||||||||||||||||||||||||||||||||
згинанні. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Обчислимо прогини балки на межах ділянок |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||

114
EJyС = EJyI |
|
x=0м = EJy0 yС = y0 = |
1286.64 |
|
= |
1286.64 103 |
= 0.0232м |
|
||||||||||||||||||||||||||
|
|
|
EJ |
|
|
|
|
5.5392 107 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
EJyD = EJyII |
|
|
|
|
|
|
|
|
|
|
30 |
7.52 |
107.5 53 |
|
|
20 |
5 |
4 |
|
|
||||||||||||||
|
|
|
=1286.64 −477.16 |
7.5 − |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
− |
|
|
|
= |
|
||||||||||
|
x |
=7.5м |
|
|
2 |
|
|
|
6 |
|
|
|
24 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
=1286.64 −3578.7 −843.75 + 2239.58 −520.83 = −1417.06 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
yD = − |
1417.06 |
= − |
1417.06 103 |
|
= −0.0256 м; |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
EJ |
5.5392 107 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
EJyB = EJyIII |
|
|
|
|
|
=1286.64 −477.16 10.5 − |
30 10.52 |
+ |
|
107.5 83 |
− |
20 84 |
− |
100 33 |
+ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
x=10.5м |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
6 |
|
|
|
24 |
|
6 |
|
|||||||||
+202434 =1286.64 −5010.18 −1653.75 +9173.33 −3413.33 −450 +67.5 =
=10527.47 −10527.26 = 0.21 ≈ 0
EJyE = EJyIV |
|
|
|
=1286.64 −477.16 12.5 − |
30 |
12.52 |
+ |
107.5 |
103 |
− |
20 10 |
4 |
− |
||||||||||||||
|
x=12.5м |
|
|
2 |
|
6 |
|
24 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
100 53 |
|
|
20 54 |
|
112.5 23 |
|
10 2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
− |
|
|
+ |
|
|
+ |
|
|
|
|
− |
|
|
=1286.64 −5964.5 −2343.75 + |
|
|
|||||||||||
6 |
|
24 |
|
6 |
|
|
24 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
+17916.67 −8333.33 −2083.33 +520.83 +150 −6.67 =1142.56 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
yE |
= |
1142.56 |
= |
1142.56 103 |
|
= 0.0206 м. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
5.5392 107 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
|
|
|
|
||||||||
Отримаємо універсальне рівняння пружної лінії для кутів повороту. Для цього продиференцюємо універсальне рівняння пружної лінії для прогинів.
|
|
VA (x −2.5)2 |
|
q1(x −2.5)3 |
|
|
|
F(x −7.5)2 |
|
||
EJy′ = EJθ = EJθ0 |
− M (x −0) |
|
+ |
− |
|
|
− |
+ |
|||
|
|
|
|||||||||
|
2! |
|
2! |
||||||||
|
|
|
|
3! |
|
|
|
|
|||
|
← |
|
I |
|
← |
|
II |
|
|
||
|
|
|
|
|
|
||||||
|
0≤x≤2.5м |
|
|
3м≤x≤5.5м |
|
|
|
|
|
||

115
|
|
+ |
q1(x −7.5)3 |
|
|
+ VB (x −10.5)2 |
− q2 (x −10.5)3 |
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
← |
|
|
|
|
|
|
|
|
|
|
III← |
|
|
IV |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
7.5м≤x≤10.5м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10.5м≤x≤12.5м |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Обчислюємо кути повороту на межах ділянок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
θC |
|
=θ0 |
= − |
477.16 |
|
= − |
477.16 103 |
|
= −0.0086 рад. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
EJ |
|
|
|
|
5.5392 |
107 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
′ |
|
|
|
′ |
|
|
|
|
|
= −477.16 −30 2.5 = −477.16 −75 = −522.16 |
|
|
|||||||||||||||||||||||||||||||||||
|
EJyA |
= EJyI |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x=2.5м |
|
|
|
|
|
|
|
|
522.16 103 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
θA = − |
522.16 |
= − |
= −0.01рад. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
5.5392 107 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
′ |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
107.5 52 |
|
|
20 53 |
|
|
|
|
|
|
|||||||||||
|
EJyD = EJyII |
|
|
|
|
|
|
|
= −477.16 −30 7.5 + |
|
|
|
|
2 |
|
− |
|
|
|
6 |
|
= |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x=7.5м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
= −477.16 −225 +1343.75 −416.67 = 224.92 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
θD |
= |
|
|
224.92 |
|
= |
|
224.92 103 |
|
= 0.0041рад. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
5.5392 107 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
′ |
′ |
|
|
|
|
= −477.16 −30 10.5 + |
107.5 82 |
− |
|
20 83 |
|
− |
|
|
100 32 |
|
+ |
20 33 |
= |
|||||||||||||||||||||||||||||
EJyB = EJyIII |
x=10.5м |
|
2 |
|
|
|
|
|
6 |
|
|
|
|
|
2 |
|
|
6 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
= −477.16 −315 +3440 −1706 −450 +90 = 581.17 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
θB |
= |
|
581.17 |
= |
|
581.17 104 |
|
= 0.0105 рад. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
5.5392 104 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
′ |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
107.5 102 |
|
|
20 103 |
|
|
|
|
100 52 |
|
20 53 |
|
|
||||||||||||||
EJyE = EJyIV |
x=12.5м |
= −477.16 −30 |
12.5 + |
|
|
2 |
|
|
|
|
|
|
− |
6 |
|
|
− |
|
2 |
|
|
+ |
6 |
+ |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
112.5 22 |
10 23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
+ |
|
|
− |
|
|
|
|
|
|
= −477.16 −375 +5375 −3333.33 −1250 + 416.67 + |
|
|
||||||||||||||||||||||||||||||||||||
2 |
|
|
|
6 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ − = θ = 567.85 = 567.85 103 =
225 13.33 567.85 E 0.0103 рад. EJ 5.5392 107
6. Побудувати пружну лінію балки і перевірити умову
жорсткості.

116
За обчисленими значеннями прогинів і кутів повороту на рис. 3.20, д побудовано пружну лінію балки. Для наочності масштаб прогинів збільшено у порівнянні з масштабом довжин у сто разів. Тому відкласти кути повороту у масштабі неможливо. При побудові пружної лінії балки необхідно враховувати такі закономірності. Опуклість пружної лінії балки завжди направлена у той бік, де розташована епюра згинальних моментів. Нульова точка епюри М є точкою перегину пружної лінії балки. В цій точці кривизна її змінює знак на протилежний.
З рис. 3.20, д видно, що стріла прогину балки f=2.56 см. Допустима стріла прогину, за умовою, складає 1/250 прольоту балки, тобто
[ f ] = |
l |
= |
8 10 |
2 |
= 3.2 см. |
|
250 |
250 |
|||||
|
|
|
||||
Так як f=2.56 см<[f]=3.2 см, то жорсткість балки забезпечена.
7. Виконати контроль обчислень на ПЕОМ згідно з інструкцією до програми ”PROCH” (див. додаток 5). Усі необхідні для вводу в ПЕОМ дані наведені нижче.
Робота 3 з опору матеріалів (задача 2)
Іванов І.І., гр.Д-21, |
|
||||
сх.-вар., par |
|
1 7 0 |
|||
Число ділянок |
|
4 |
|||
Номери опорних точок |
2 4 |
||||
----------------------------------------- |
|||||
N в.| Xi[м] |
Mi[кнм] Fі[кн] qi[кн/м] |
||||
----------------------------------------- |
|||||
1 |
| |
0.00 |
-30.00 |
0.00 |
0.00 |
2 |
| |
2.50 |
0.00 |
0.00 |
-20.00 |
3 |
| |
7.50 |
0.00 |
-100.00 |
0.00 |

117
4 |
| 10.50 |
0.00 |
0.00 |
-10.00 |
|
5 |
| 12.50 |
0.00 |
0.00 |
|
0.00 |
Контрольні дані |
h, y5, t5 |
0.450 0.0206 0.0102 |
|||
Максимальні зусилля Mmax, Qmax 257.50 107.50
Результати обчислень на ПЕОМ за програмою ”PROCH”, що виконані згідно з інструкцією (див. додаток 5), наведені на рис. 3.22.
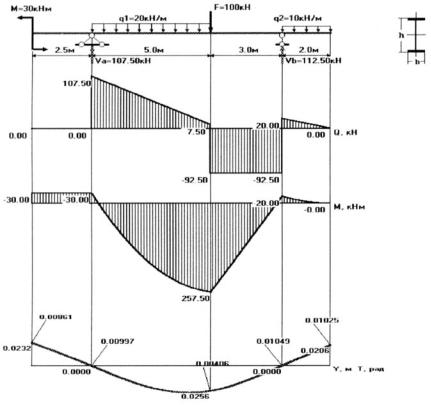
118
Задача 2. Розрахунок сталевої двотаврової балки
Результати розрахунку
Опорні реакції Va=107.50кН Vb=112.50кН
|M|max=257.50кНм при Х=7.50м |Q|max=107.50кН при Х=2.50м
Розміри двотаврового перерізу
W=0.001197м3=1197см3 I№45 Ц*=1231см3 J*=27696см4 h=0.45м b=0.160м d=0.009м t=0.0142м
Максимальні напруження для перерізу Smax=209.18МПа не перевищує допустимі напруження Tmax= 30.53МПа не перевищує допустимі напруження Небезпечні і еквівалентні напруження для перерізу
Sнеб=195.99МПа Топ= 18.37МПа Sекв=198.55МПа
Початкові параметри EIY0=1286.72кНм3 EIT0=-477.19кНм2
Жорсткість при згині EJ=55392кНм2 Стріла прогину f=0.02738м при Х=6.60м Умова жорсткості виконується f<[f]=0.0320м
Виконав на ПЕОМ ст. Іванов І.І., гр.Д-21, сх.-вар. 1 7
Рис. 3.22
119
3.5. Приклади для самостійного розв’язання
Приклад 3.13. У поперечному перерізі балки (рис. 3.23) діють згинальний момент Mz=-30 кНм і поперечна сила Qy=70 кН. Визначити нормальні і дотичні напруження в точках А і В.
100 |
15 |
|
|
|
|
|
|
A |
|
F=30кН |
q=12кН/м |
|
A |
|
B |
|
|
|
|
|
200 |
|
|
B |
2м |
1м |
0.75м |
50 |
|
|
|
10 |
|
|
|
Рис. 3.23 |
|
Рис. 3.24 |
|
Приклад 3.14. Для балки (рис. 3.24) підібрати двотавровий поперечний переріз при [σ]=140 МПа, [τ]=100 МПа.
Приклад 3.15. Для балки (рис. 3.25) підібрати прямокутний поперечний переріз зі співвідношенням сторін h/b=3, якщо [σ]=140 МПа, [τ]=100 МПа.
Приклад 3.16. Для балки (рис. 3.26) підібрати круглий поперечний переріз, якщо Rзг=14 МПа, Rск=2.2 МПа, n=1.1, m=0.9.
q=6кН/м q=6кН/м q=4кН/м
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5м |
1.5м |
||||||||||||||||||||||
|
2м |
|
|
|
|
|
|
4м |
|
|
|
|
2м |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.25 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.26 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Приклад 3.17. Визначити прогин і кут повороту кінцевого перерізу В консолі (рис. 3.27).
Приклад 3.18. Визначити прогин перерізу С балки (рис. 3.28). Приклад 3.19. Визначити прогин перерізу С і кут повороту перерізу D
балки (рис. 3.29).
