
- •4.1. Просторове та косе згинання. Основні відомості з теорії
- •Далі обчислюємо за формулою (5.2) гнучкість стійки
- •Рис. 6.3. Ефективний коефіцієнт концентрації напружень:
- •1 – при згинанні; 2 – при крученні
- •Рис. 6.15. Коефіцієнт якості поверхні при:
- •Далі визначимо
- •Таблиця 6.3
- •ДОДАТКИ
- •ДОДАТОК 1
- •Відповідальний за випуск В.В. Буланов
- •Редактор О.Ю. Цигіпова
K` |
|
|
|
|
|
|
|
r |
t |
|
|
|
|
|
|
|
D |
|
d |
2.0 |
|
1 |
|
|
|
|
|
t/r=1 |
|
|
|
|
|
|
1.5 |
2 |
|
|
|
|
|
|
|
|
1.0 |
|
|
|
r/d |
0 |
0.1 |
0.2 |
|
0.3 |
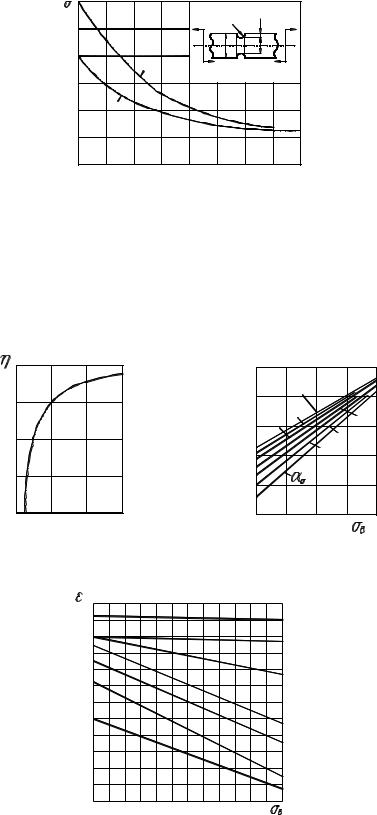
Рис. 6.12. Ефективний коефіцієнт концентрації напружень при: 1 – σ = 1000 МПа; 2 – σ = 500МПа
Вплив чистоти оброблення поверхні деталі на межу витривалості оцінюється в практичних розрахунках на витривалість коефіцієнтом якості поверхні εп . Для його визначення можна скористатися графіками, наведеними
на рис. 6.15.
1.00 |
|
|
|
0.75 |
|
|
|
0.50 |
|
|
|
0.250 |
1 |
2 |
t/r |
q |
|
|
|
0.8 |
1.8; 1.9; 2.0 |
|
|
|
|
|
|
|
1.7 |
|
1.5 |
0.6 |
1.6 |
|
|
1.4 |
|
||
|
|
||
|
|
|
|
0.4 |
|
1.3 |
|
|
|
|
|
0.2 |
|
=1.2 |
|
|
|
|
|
0 |
|
|
|
400 |
600 |
800 |
, МПа |
Рис. 6.13. Поправковий коефіцієнт на |
Рис. 6.14. Коефіцієнт чутливості матеріалу |
відношення t/r до рис. 6.12 напружень |
до концентрації |
п |
|
|
2 |
1.0 |
1 |
0.8 |
3 |
|
|
0.6 |
4 |
0.4 |
5 |
|
6
0.2 |
7 |
|
0300 500 700 900 1100 1300 , МПа
Рис. 6.15. Коефіцієнт якості поверхні при:
1 – шліфованій; 2 – полірованій; 3 – після чистової обробки; 4 – грубо обточеній; 5 – після прокатки; 6 – кородованій в прісній воді;
7 – кородованій в морський воді поверхні
150
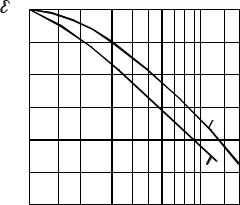
Межа витривалості матеріалу в значній мірі залежить від абсолютних розмірів деталі. Зі збільшенням розмірів деталі межа витривалості матеріалу зменшується. Це враховується в практичних розрахунках на витривалість спеціальним коефіцієнтом εМ , що називається масштабним фактором. Його
значення можна визначити за графіками, наведеними на рис. 6.16.
м |
|
|
|
|
|
0.9 |
|
|
|
|
|
0.8 |
|
|
|
|
|
0.9 |
|
|
|
1 |
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
0.5 |
|
|
|
2 |
|
|
|
|
|
|
|
0.410 |
15 |
20 |
30 |
40 506070 80100150 |
d, мм |
Рис. 6.16. Масштабний фактор для: 1 – вуглецевих сталей; 2 – легованих сталей
Графіками, наведеними на рис. 6.15 і рис. 6.16, можна користуватися як при згинанні, так і при крученні.
Вплив усіх факторів, що знижують межу витривалості матеріалу, враховується загальним коефіцієнтом зниження межі витривалості при симетричному циклі
K |
σд |
= |
Kσ |
або K |
τд |
= |
Kτ |
. |
(6.13) |
εnεM |
|
||||||||
|
|
|
|
εnεM |
|
||||
Усі розрахунки на міцність при дії повторно-змінних напружень виконуються як перевірочні. Спочатку при знижених допустимих напруженнях визначають з умов міцності розміри поперечних перерізів елементів без урахування циклічної дії напружень. Потім визначають усі коефіцієнти зниження міцності при втомленості й обчислюють фактичний коефіцієнт запасу міцності n. Міцність вважається забезпеченою, якщо виконується умова міцності
n ≥[n], |
(6.14) |
де [n] – необхідний або нормативний коефіцієнт запасу міцності при втомленості. Він приймається в межах від 1,4 до 3.
Фактичний коефіцієнт запасу міцності при втомленості визначається в залежності від типу напруженого стану і асиметрії циклу за однієї з таких формул:
а) при лінійному напруженому стані і симетричному циклі
151

nσ = |
σ−1 |
; |
(6.15) |
|
Kσд σmax |
||||
|
|
|
б) при лінійному напруженому стані і асиметричному циклі
nσ = |
|
σ−1 |
– за втомленістю, |
(6.16) |
||
Kσд σα + ψσσc |
||||||
|
|
|
||||
n |
= |
σт |
– за текучістю, |
(6.17) |
||
|
||||||
σт |
|
σmax |
|
|
||
де ψσ = σ− 1 – коефіцієнт чутливості матеріалу до асиметрії циклу.
σв
При інших способах спрощення діаграми граничних напружень рекомендується приймати в залежності від σв значення коефіцієнтів ψσ і ψτ ,
що наведені нижче в табл. 6.1 [1].
Таблиця 6.1
σв, МПа |
ψσ |
ψτ |
350-550 |
0 |
0 |
520-750 |
0,05 |
0 |
700-1000 |
0,10 |
0,05 |
1000-1200 |
0,20 |
0,10 |
1200-1400 |
0,20 |
0,15 |
При σс <0 приймають ψσ =0.
При плоскому напруженому стані і асиметричному циклі зміни напружень коефіцієнт запасу міцності при втомленості визначається за формулою
n = |
nσnτ |
, |
(6.18) |
|
n2 |
+ n2 |
|||
|
σ |
τ |
|
|
де nσ і nτ – коефіцієнт запасу міцності при втомленості відповідно за
нормальними і дотичними напруженнями.
При синхронній зміні напружень σ і τ коефіцієнти nσ і nτ можна
визначити за формулами (6.15) – (6.17). Ці формули застосовують і при крученні, якщо в них замінити σ на τ.
152
6.2. Приклади розрахунків деталей машин на витривалість
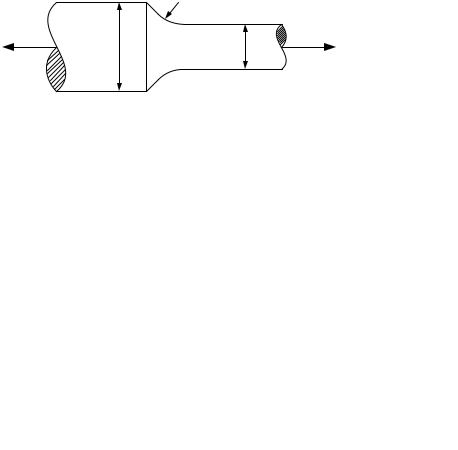
Приклад 6.1. Східчастий стержень (рис. 6.17) зі сталі 50Г2 (σв =750 МПа)
навантажений осьовою силою, що змінюється за симетричним циклом. Поверхня стержня шліфована. Визначити допустиме значення амплітуди осьової сили при [n]=2.
Рис. 6.17
За графіком на рис. 6.7 знаходимо ефективний коефіцієнт концентрації напруженьKσ ≈ 1,62 при r/d = 0,16 і σв = 750 МПа.
Коефіцієнти якості поверхні і масштабний фактор знаходимо за графіками на рис. 6.15 і рис. 6.16: εп =0,93 і εм =0,81.
Далі обчислюємо за формулою (6.13) загальний коефіцієнт зниження міцності при втомленості
K |
σд |
= |
Kσ |
= |
1,62 |
|
= 2,15 , |
|
0,93 0,81 |
||||||
|
|
εпεм |
|
||||
а за формулою (6.5) – межу витривалості при симетричному циклі при розтяганні-стисканні
σ−0 1 =0,28·σв = 0, 28 750 = 210 МПа.
Тепер, використовуючи формулу (6.15) і умову (6.14), одержимо
|
|
|
|
n = |
σ0 |
|
|
= |
|
σ0 |
|
|
≥ [n]. |
||
|
|
|
|
− 1 |
|
|
− 1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
σ |
Kσд σmax |
|
|
Fmax |
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Kσд A |
|
|
||
Звідси знаходимо |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
σ0 |
πd 2 |
|
|
= 210 10 |
6 |
3,14 |
0,05 |
2 |
|
|
|||
|
|
|
|
|
|
|
|||||||||
F |
≤ |
− 1 4 |
|
|
|
|
= 95843H ≈ 95,8кН. |
||||||||
|
|
|
|
|
|
|
|
|
|||||||
max |
|
Kσд [n] |
|
4 2,15 2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
Приймаємо [Fmax]=95,8 кН.
Приклад 6.2. Перевірити міцність на втомленість сталевого стержня круглого поперечного перерізу (рис. 6.18, а), якщо в небезпечному перерізі
153
