7 лаб / Где квадрат

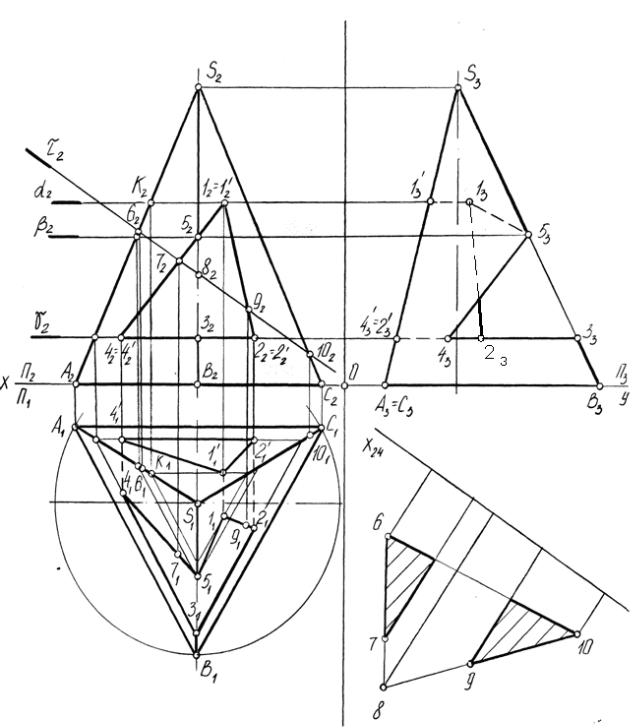
21

Z

Рис. 13. Взаимное пересечение многогранников (пирамиды с призматическим отверстием)

22

Опорные точки заданного призматического отверстия отмечены на фронтальной проекции пирамиды. Положение горизонтальных проекций этих точек определено с помощью вспомогательных секущих плоскостей , и .

Для построения точек 1 и 1' проведена вспомогательная горизонтальная плос-

кость , которая пересекла грани пирамиды по прямым, образующим тре-

угольник, подобный треугольнику АВС, лежащему в основании пирамиды.

Для построения треугольника использовали точку К – точку пересечения се-

кущей плоскости с ребром SА. На горизонтальной плоскости П1 проекция треугольника проходит через К1 параллельно сторонам основания пирамиды.

На пересечении линий связи, проведенных из 12 и 1'2, с горизонтальной проек-

цией найденного сечения получены 11 и 1'1.

Аналогично построены горизонтальные проекции остальных точек, что-

бы найти точки 2, 2', 3, 4 и 4' проведена вспомогательная секущая плоскость ,

а для точки 5 – плоскость . Полученные проекции точек соединены последо-

вательно в ломаную линию.

Профильные проекции 1'3, 2'3, 3'3 определены по их принадлежности гра-

ни ASC, проекции 33 и 53 лежат на проекции ребра S3В3, а проекции точек 13 и

43 построены с помощью ординат у или по линиям проекционной связи.

Натуральная величина фигуры сечения пирамиды фронтально проеци-

рующей плоскостью определена также способом замены плоскостей проекций,

но перенесена на свободное поле чертежа, используя правила параллельного переноса.

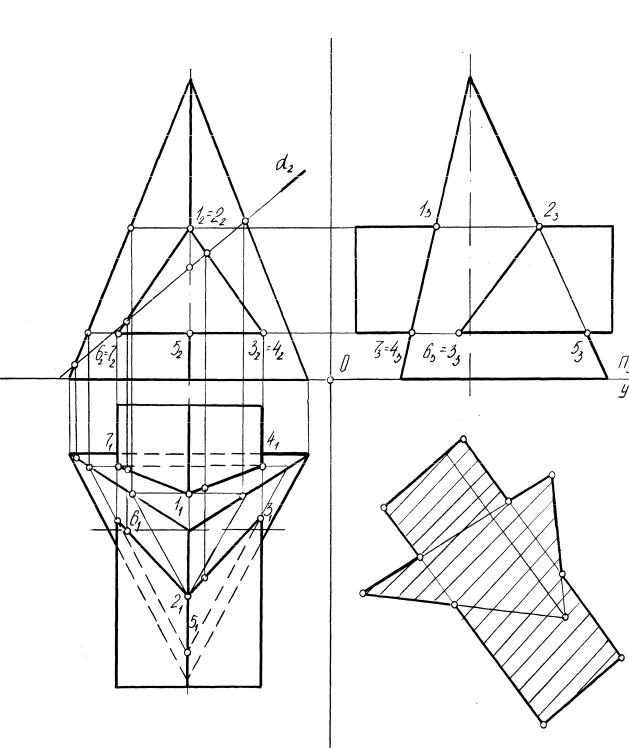
Пример построения линии пересечения прямой трехгранной призмы и прямой трехгранной пирамиды рассмотрен на рис. 14. Определены опорные точки пространственной линии пересечения как результат пересечения ребер призмы с ребрами и гранями пирамиды. Построения аналогичны предыдущим.

23

Z

Рис. 14. Взаимное пересечение многогранников (призмы и пирамиды)

24

6. Рекомендации по выполнению и оформлению графической работы теме "Взаимное пересечение многогранников"

Цель работы

Закрепление умений и навыков по выполнению на комплексном чертеже

следующих решений и построений:

1.Построение многогранника на комплексном чертеже по координатам его вершин.

2.Нахождение линии взаимного пересечения двух многогранников.

3.Определение натуральной величины фигуры сечения взаимно пересе-

кающихся многогранников.

Оформление работы

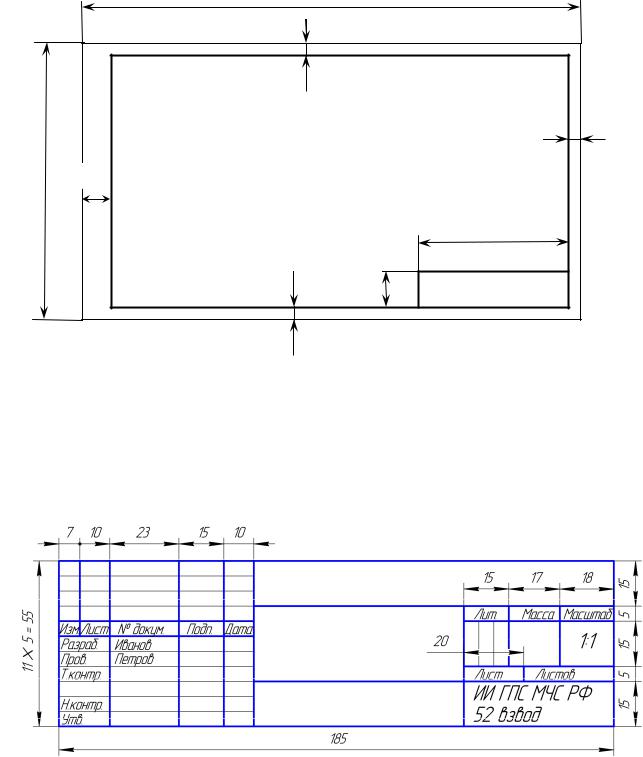
1.Работа выполняется на листе ватмана формата А3 (297 420 мм).

2.Согласно требованиям ГОСТ 2.301-68 лист ватмана оформляют рам-

кой на расстоянии от левой границы формата 20 мм, от трех других сторон на расстоянии 5 мм (рис. 15), а также сопровождают основной надписью по ГОСТ

2.104 – 68 (рис. 16).

3. Все изображения на чертеже выполняются только карандашом, ли-

ниями различного типа согласно ГОСТ 2.303-68; надписи на чертеже выпол-

няют чертежным шрифтом в соответствии с ГОСТ 2.304-81.

4.Варианты заданий выдаются преподавателем индивидуально.

5.В основной надписи указывают тему графической работы: "Взаимное пересечение многогранников".

26

Содержание графической работы по теме

"Взаимное пересечение многогранников"

1.В масштабе 1 : 1 согласно своего варианта перечертить две проекции двух взаимно пересекающихся многогранников. На фронтальной плоскости проекций П2 нанести линию секущей плоскости (А-А), как указано на задании.

2.По двум заданным проекциям многогранника построить третью про-

екцию. На трехкартинном комплексном чертеже найти линию взаимного пере-

сечения поверхностей двух многогранников, определить видимость этой линии

идругих элементов многогранников.

3.Определить натуральную величину фигуры сечения двух пересекаю-

щихся многогранников, полученную от фронтально-проецирующей плоскости А-А. Задачу решить методом замены плоскостей проекций.

Пример оформления графической работы "Взаимное пересечение много-

гранников" приведен на рис. 17.

28

7.СПИСОК ЛИТЕРАТУРЫ

1.Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геомет-

рии. – М.: Высшая школа, 2000. – 272 с.

2.Локтев О.В. Краткий курс начертательной геометрии. – М.: Высшая школа, 1999. – 136 с.

3.Крылов Н.Н. Начертательная геометрия. – М.: Высшая школа, 2000. –

224 с.

29

Легкова Ирина Анатольевна Никитина Светлана Александровна

МНОГОГРАННИКИ

Методические указания для курсантов и слушателей 1 курса специальности 280104.65

Редактор Ю.В. Шмелева

____________________________________________________________________

Подписано в печать

____________________________________________________________________

Отделение организации научных исследований Ивановского института ГПС МЧС России 153040, г. Иваново, пр. Строителей, 33