7 лаб / 376_Leksiya13

Л Е К Ц И Я 13

ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ ПЛОСКОСТЬЮ ЧАСТНОГО ПОЛОЖЕНИЯ И РАЗВЕРТКА ПОВЕРХНОСТИ

УСЕЧЕННОЙ ЧАСТИ

П л а н:

1. Общие сведения

2. Пересечение призмы плоскостью и развертка поверхности

3. Пересечение пирамиды плоскостью и развертка поверхности

1. Общие сведения

При пересечении многогранника плоскостью в сечении по­лучается плоский многоугольник. Число сторон и вершин мно­гоугольника равно соот­вет­ственно числу пересеченных плос­костью граней и ребер многогранника. Построение плоского се­чения многогранника сводится к нахождению точек пересечения ребер с секущей плоскостью. При этом очень важно опреде­лить заранее, какая фигура получится в сечении, тогда по­строение будет выполнено более верно.

Истинную величину фигуры сечения находят способом совме­щения или замены плоскостей проекций.

2. Пересечение призмы плоскостью

и развертка поверхности

В зависимости от положения плоскости, пересекающей призму, фигурой сечения может быть:

1) многоугольник, равный основанию призмы, если секущая плоскость параллельна основанию (рис. 80, а);

2) многоугольник, не равный основанию призмы, если секу­щая плоскость наклонена к основанию (рис. 80, б);

3) параллелограмм, если секущая плоскость параллельна боковым ребрам призмы. В сечении прямой призмы плоскостью, параллельной ее ребрам, полу­чается прямоугольник (рис. 80, в).

На рис. 81 показано пересечение прямой шестиугольной призмы фрон­таль­но-проецирующей плоскостью Р, построение проекций линии пересечения, нахож­дение натуральной величи­ны фигуры сечения, построение развертки и аксонометрической проекции усеченной части.

Для построения линии пересечения найдены точки пересече­ния ребер призмы с плоскостью Р (рис. 81, а). Так как плос­кость Р проецирующая, фрон­тальные проекции 1', 2', …, 6' этих точек совпадают со следом P_v, а фигура сечения изображается на плоскости V отрезком 1'-4'. Горизонтальные проекции этих точек совпадают с горизонтальными проекциями ребер (I ≡ а, 2≡b и т. д.). Следовательно, горизонтальная проекция фигуры сечения совпадает с одноименной проекцией основания призмы. Для построения профильной проекции фигуры сечения доста­точно найти профильные проекции 1", 2",… 6" ее точек и по­следовательно соединить их отрезками прямых.

Истинная величина фигуры сечения найдена способом заме­ны плоскостей проекций. Секущая плоскость Р принята за но­вую плоскость проекций Н₁, а след P_v – за новую ось проек­ций. Из точек 1' 2'…, 6' проведены перпендику-ляры к P_v, как линии связи в новой системе плоскостей проекций, и на них отложены ординаты точек I, II,…, VI, т. е. отрезки I'I₁, равный а'а, 2'2₁, равный b'b, и т. д. Полученный шестиугольник 1', 2', …, 6' определяет истинную величину фигуры сечения.

Развертка поверхности усеченной части призмы состоит из развертки боковой поверхности, основания и фигуры сечения (рис. 81, б). Вначале строят развертку поверхности целой приз­мы. Затем на ней находят точки I₀, 1I', …,..... VI₀, откладывая от­резки A_oI₀=a'l¹, В₀П₀=b'2' и т. д. Линия пересечения на раз­вертке изображается ломаной I ₀II_о ... IV_q. Фигуру сечения при­страивают к одному из отрезков этой ломаной линии, а основа­ние призмы – к основанию одной из граней.

Аксонометрическую проекцию усеченной части этой призмы можно по­строить по координатам. Для этого ось оz совмещают с осью симметрии призмы и строят аксонометрическую проек­цию основания (рис. 81, в). Из вер­шин шес­тиугольника про­водят прямые, параллельные оси оz, и откладывают на них ко­ординаты z точек пересечения ребер плоскостью Р (А1=а'1' ВП=b'2' и т. д.). Соединив полученные точки I, II,…, VI от­резками прямых, завершают построение.

3. Пересечение пирамиды плоскостью

и развертка поверхности

В зависимости от поло­жения секущей плоскости фигурой сечения пира­ми­ды может быть:

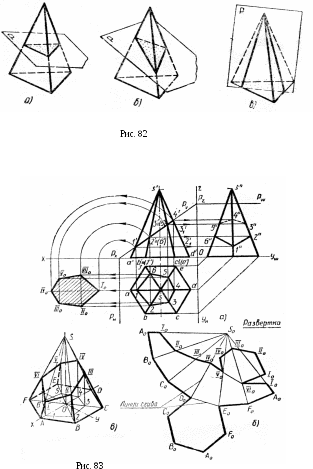
1) многоугольник, подобный основанию, если секущая плос­кость парал­лель­на основанию (рис. 82, а);

2) многоугольник, не подобный основанию, если секущая плоскость накло­не­на к основанию (рис. 82, б);

3) треугольник, если секущая плоскость проходит через вер­шину пира­миды (рис. 82, в).

На рис. 83 показано пересечение правильной шестиуголь­ной пирамиды фронтально-проецирующей плоскостью Р, по­строение проекций линии пересе­че­ния поверхности, нахождение истинной величины фигуры сечения, построе­ние развертки и ак­сонометрической проекции усеченной части.

Фронтальные проекции 1', 2', …, 6' точек I, II, …, VI пересе­чения ребер пирамиды плоскостью Р лежат на следе Pv, фигура сечения изображается на плоскости V отрезком 1'-4', совпада­ющим с этим следом. Горизонтальные проекции 1, 2, .... 6 этих точек находятся в пересечении линий связи, проведенных из фронтальных проекций 1', 2', …, 6', с горизонтальными про­екциями sa, sb, …, sf ребер пирамиды. Горизонтальной проек­цией фигуры сечения является неправильный шестиугольник 1-2-3- ... -6. Для построения профильной проекции сечения нахо­дят профильные проекции его точек 1", 2", 6", которые со­единяют отрезками прямых.

Истинная величина I_qII_qIII₀IV₀V_qVI₀ фигуры сечения найдена способом совмещения. Плоскость Р вместе с фигурой сечения совмещена с плоскостью Н вращением вокруг следа Р_Н.

Для построения развертки усеченной части вначале строят раз­вертку поверхности полной пирамиды (рис. 83, б). Так как пира­мида правильная, то ее боковыми гранями являются равнобедрен­ные треугольники, а основанием — правильный шестиугольник. Следовательно, развертка поверхности пирамиды будет фигурой, состоящей из шести треугольников и одного шестиугольника. Длина боковых ребер определяется по фронтальной проекции, т. е. SA=SB = ...=SF=s'a'=s'd'. Расстояния точек пересечения ребер пирамиды плоскостью Р от вершины S определяют враще­нием этих ребер вокруг оси симметрии пира­миды, располагая их параллельно плоскости V. Практически для этого доста­точно из фронтальных проекций 2'≡6' и 3'≡5' провести прямые па­раллельно оси ох до пересечения с проекцией s'd' в точках 2₁' и 3₁'. Тогда расстояния SII=SVI=s'2₁' и SIII=SV=s'3_l', а расстояния SI=s'1' и SIV=s'4' определяются без дополни­тельных построений. Найденные расстояния откладывают на изобра­же­ниях соответствующих ребер и соединяют полу­чен­ные точки I₀, П₀,…, VI₀ ло­ма­ной линией. Фигуру сечения пристраи­вают к од­но­му из отрезков этой ло­ма­ной линии.

Аксонометрическую проекцию усеченной части пирамиды, так же как и призмы, строят по координатам. Для этого ось оz совмещают с осью симметрии пирамиды и строят первичную аксонометрическую проекцию АВ... F основания и вторичную проекцию 1-2- ... -6 фигуры сечения (рис. 83, в). Из ее вер­шин 1, 2,…, 6 проводят прямые параллельно оси оz и на них от­кладывают координаты оz точек пересечения ребер плоскостью Р. Соединив найденные точки I, II, …, VI последовательно отрез­ками прямых, получают аксонометрическую проекцию фигуры сечения, а соединив их с точками А, В,…, F,– аксонометриче­скую про­ек­цию боковых ребер.