Метод моментов

Суть метода в том, что начальные и центральные эмпирические моменты являются состоятельными оценками соответственного начальных и центральных теоретических моментов того же порядка, например,

Учитывая, что теоретические моменты выражаются через параметры распределения, и используя равенство моментов, получим уравнения (системы уравнений), содержащих искомые параметры. Решение уравнений (систем уравнений) и будет оценками неизвестных параметров.

Если распределение определяется одним параметром, то достаточно составить одно уравнение, если двумя, то два уравнения и т.д. Сколько параметров, столько должно быть и уравнений.

Метод максимального правдоподобия

Метод опирается на использование условий экстремума функции одной или нескольких переменных.

В качестве такой функции принимают функцию правдоподобия.

Для ДСВ : гдеварианты выборки,параметр, для которого находится оценка,вероятность событиязависящая от параметра

Для НСВ : гдезаданная функция плотности вероятности в точках

Так как функция и достигают максимума при одном и том же значениито обычно точки экстремума находятся для

Чаще всего данный метод используется при биномиальном, пуассоновском и показательном распределениях случайной величины .

Если неизвестное распределение случайной величины имеет один параметр то функцияфункция одной переменной

Алгоритм нахождения точки максимума:

• вычислить производную

• найти критическую точку из условия

• определить знак на интервалах или найтии вычислить ее значение в точке

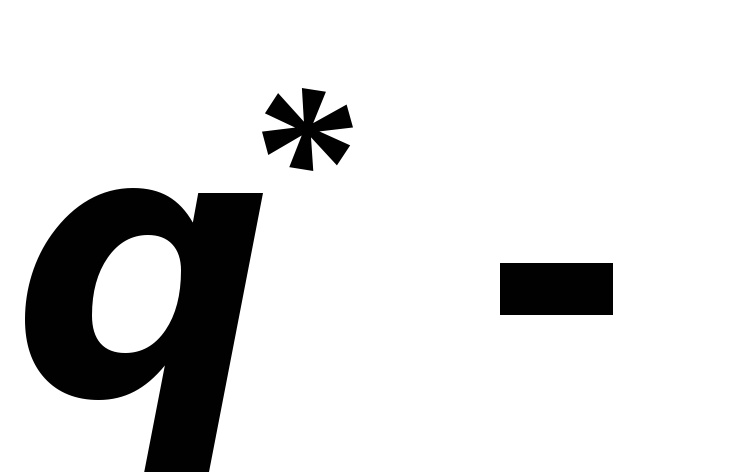• если значение в точкеотрицательное, тоточка максимума ипринимают в качестве оценки параметра

Если неизвестное распределение случайной величины содержит два параметра, то значения находят как экстремум функции двух переменных.

Интервальные оценки

Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.

Интервал, в который попадает оцениваемый параметр с заданной надежностью , называют, доверительным.

Примеры доверительных интервалов для параметров нормальной случайной величины .

1. Доверительный интервал для математического ожидания нормальной случайной величины Х при известном среднеквадратическом отклонении

где точность оценки числоопределяется из

равенства илипотаблице Лапласа (приложение 1).

2. Доверительный интервал для математического ожидания нормальной случайной величины при неизвестной дисперсии (среднеквадратическом отклонении), а известна исправленная дисперсия гденайдем по таблицераспределения Стьюдента (приложение 1) по заданным и

3. Доверительный интервал для среднего квадратического отклонения нормально распределенной случайной величины по исправленному выборочному отклонению :

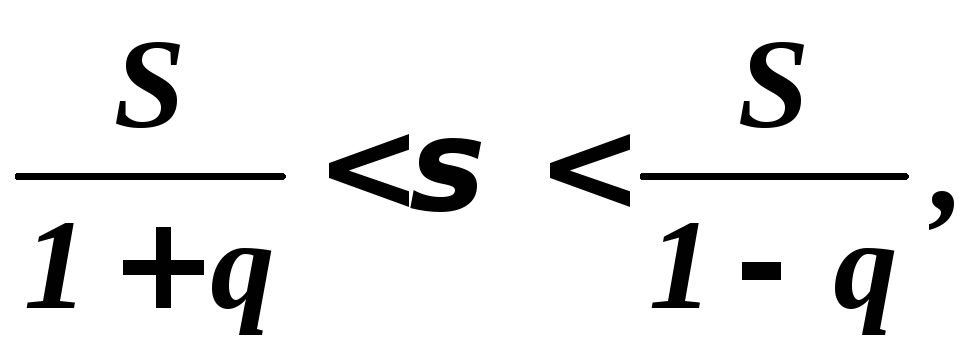
где – параметр, который находят по таблице значений(приложение 1).

4. Доверительный интервал для дисперсии нормально распределенной случайной величины при неизвестном :

где