Эмпирическая функция распределения

Функция илиназывается эмпирической функцией распределения.

								1

Функция неубывающая, ее график имеет ступенчатый вид, т.е. представляет собой отрезки прямых, параллельных оси абсцисс, длина отрезков:расстояние от отрезков до оси абсцисс:

Функция служит оценкой неизвестной функцией распределеният.е.

Оценкой для плотности распределения непрерывной случайной величины (признака ) служит гистограмма частот (частостей).

10. Выборочные характеристики статистических распределений

Для описания основных свойств статистических распределений используют выборочные характеристики двух видов: средние и вариации (рассеяния).

К средним относятся:

• средняя арифметическая:

(10.1)

Применяется к вариационному ряду с несгруппированными данными наблюдения;

• взвешенная средняя арифметическая (частоты и частостиназывают весами):

(10.2)

или

(10.3)

Применяется к ранжированному вариационному ряду дискретного признака Х.

• медиана – это серединное значение признака Х, по определению

	(10.4)
если четное;	(10.5)
если нечетное.	(10.6)

• мода – наиболее часто встречающееся значение признака .

если

Характеристики вариации

• Выборочная дисперсия:

(10.7)

Применяется к вариационному ряду с несгруппированными данными наблюдения.

• Выборочная взвешенная дисперсия:

(10.8)

Применяется к вариационному ряду со сгруппированными данными наблюдения.

• Средний квадрат – выборочная средняя арифметическая квадратов значений признака .

	(10.9)
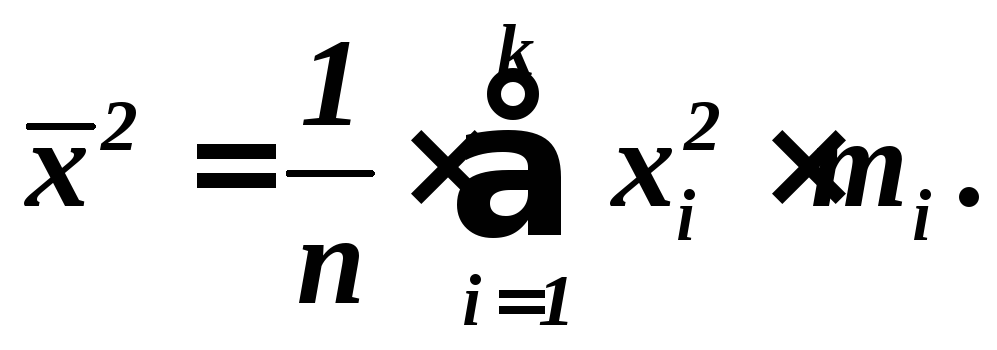
	(10.10)

Наиболее часто применимая формула для

(10.11)

• Выборочное среднее квадратическое отклонение:

  (10.12)

• Размах вариации:

  (10.13)

• Коэффициент вариации:

(10.14)

11. Оценивание параметров

Пусть оценка некоторого теоретического параметразакона распределения случайной величины .

Оценки параметров бывают точечные и интервальные.

Точечные оценки

Если статистическая оценка характеризуется одним числом, она называется точечной.

К числу точечных оценок относятся выборочная средняя и выборочная дисперсия.

Свойства оценок

1. Несмещенность. Если математическое ожидание статистической оценки равно оцениваемому параметру генеральной совокупности, то такая оценка называется несмещенной, если не равно, то смещенной.

2. Эффективность. Эффективной называется статистическая оценка, которая при одних и тех же объемах выборки имеет наименьшую дисперсию.

3. Состоятельность. Состоятельной называется статистическая оценка, которая при увеличении объема выборки стремится по вероятности к оцениваемому параметру

Точечной оценкой для математического ожидания случайной величины служит выборочное среднее.

Выборочное среднее является состоятельной, несмещенной и эффективной оценкой для:

(11.1)

Точечными оценками для дисперсии случайной величины Х являются выборочная дисперсия и исправленная выборочная дисперсия:

(11.2)

Состоятельные оценки дисперсии являются: смещенной, анесмещенной.

Для среднего квадратического отклонения существует две точечные оценки: смещенная –и несмещенная

(11.3)

Точечные оценки неизвестных параметров заданного распределения могут быть определены с помощью метода: моментов и метода максимального правдоподобия.