Закон распределения Пуассона

Дискретная случайная величина имеет закон распределения Пуассона, если она принимает значения (бесконечное, но счетное множество) с вероятностями

	(7.8)
	(7.9)
	(7.10)
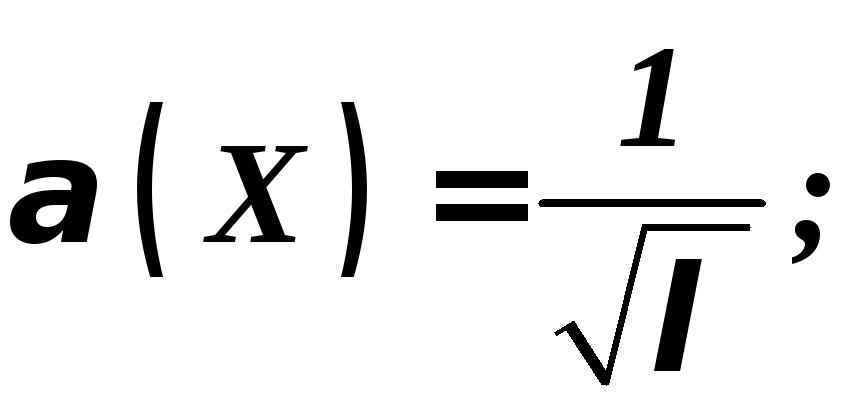
	(7.11)
	(7.12)

определить по таблице.

Геометрическое распределение

ДСВ имеет геометрическое распределение, если она принимает значения (бесконечное, но счетное множество) с вероятностями

(7.13)

Характеристики:

	(7.14)
	(7.15)

Гипергеометрическое распределение

ДСВ имеет гипергеометрическое распределение, если она принимает значения с вероятностями

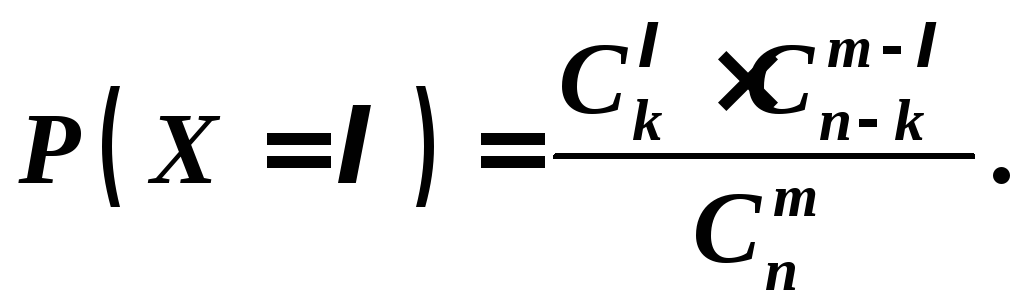
(7.16)

Характеристики:

	(7.17)
	(7.18)

8. Непрерывные распределения

Название распределения	Функция распределения (закон, график)	Плотность распределения (закон, график)	Параметр	Числовые характеристики
Равномерный закон			а, b
Показательный закон
Нормальный закон

9. Статистические распределения

Набор значений случайной величины , полученных в результате статистического наблюдения, называется выборкой объема и образует вариационный ряд, при этом называют вариантами.

Вариационный ряд с расположенными по возрастанию вариантами называют ранжированным вариационным рядом.

Если вариационный ряд содержит различных вариант, причем каждая варианта встречаетсяраз, то числоназывается частотойа отношениеназывается относительной частотой:.

Изучаемый признак может быть дискретным, т.е. его значения отличаются на конечную, заранее известную величину (год рождения, тарифный разряд, число предприятий), или непрерывным, т.е. его значения отличаются на сколь угодно малую величину (время, вес, стоимость).

Вариационный ряд для дискретного признака принято наглядно и компактно представлять в виде таблицы, в первой строке которой указаны различных значений изучаемого признака, а во второй строке – соответствующие этим значениям частоты

Статистическим (выборочным) распределением называется последовательность пар

			…
			…

Статистическое распределение для непрерывного признака принято представлять интервальным рядом – таблицей, в первой строке которой указаны интервалов значений изучаемого признака в виде , а во второй строке – соответствующие этим интервалам частоты.

Для непрерывного признака частота число различныхпопавших в соответствующий интервал:

Четыре возможные формы представления статистических распределений.

Дискретный ряд частот:

			…
			…

Интервальный ряд частот:

			…
			…

Дискретный ряд частостей:

			…
			…

Интервальный ряд частостей:

			…
			…

Графическое представление статистических распределений: полигон и гистограмма.

Дискретный ряд изображают в виде полигона.

Полигон частот (частостей) – ломаная линия, отрезки которой соединяют точки с координатами

Интервальный ряд изображают в виде гистограммы.

Гистограмма частот есть ступенчатая фигура, состоящая из прямоугольников, основания которых – интервалы длинной, а высоты – плотности частотГистограмма относительных частот – ступенчатая фигура, состоящая из прямоугольников с основаниямии высотамиНа практике чаще всего полагают величинуодинаковой для всех интервалов:где