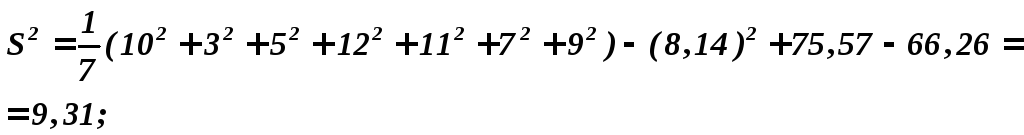- •Теория вероятностей и математическая статистика
- •1. Вычисление вероятности события по классической формуле .
- •2. Вычисление вероятности событий по известным вероятностям других событий, с ними связанных.
- •3. Вычисление вероятности события по формуле полной вероятности
- •4. Построение многоугольника распределения дискретной случайной величины по ее ряду распределения
- •5. Вычисление вероятности попадания случайных величин х подчиненной нормальному законуна заданный интервал
- •1.Решения задач, когда все элементарные события равновероятны:.
- •Решение
- •2. Подсчет геометрических вероятностей:
- •Решение
- •3. Вероятности, связанные с подсчетом числа перестановок:
- •Решение
- •4. Вероятности, связанные с подсчетом числа размещений: .
- •Решение
- •5. Вероятности, связанные с подсчетом числа сочетаний:
- •Решение
- •6. Независимые события .
- •Решение
- •7. Формула полной вероятности:
- •Решение
- •8. Формула Байеса:
- •Решение
- •9. Математическое ожидание , дисперсия, стандартное отклонениедискретной случайной величины.
- •Найти математическое ожидание , дисперсию ,, вероятности .
- •Решение
- •13. Математическое ожидание , дисперсия,стандартное отклонение, вероятностиравномерного распределения.
- •Решение
- •Решение
- •Решение
- •2. Вычисление точечных оценок параметров распределения по выборке
- •Решение
- •Решение
- •3. Вычисление доверительных интервалов для среднего
- •Решение
- •4. Вычисление доверительного интервала для вероятности наступления событияс помощью таблиц нормального распределения.
- •Решение
- •Решение
- •5. Проверка статистических гипотез
- •Решение
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму | ||||||||||||||||||||||||||||||||||
|
1 |
Упорядочить заданные значения по возрастанию, сосчитать их количество |
| ||||||||||||||||||||||||||||||||||
|
2 |
Сгруппировать значения, если надо; сосчитать число значений, попавших в интервалы разбиения; вычислить эмпирические частоты, составить таблицу эмпирического распределения |
Таблица частот появления значения
Таблица эмпирического распределения
| ||||||||||||||||||||||||||||||||||
|
3 |
По таблице эмпирического распределения нарисовать гистограмму и полигон, найти медиану |
Гистограмма и полигон Медиана 8,375 (делит площадь гистограммы пополам). |
2. Вычисление точечных оценок параметров распределения по выборке
|
Умения |
Алгоритм действий |
|
Вычисление точечных оценок параметров распределения по выборке |
1. Выписать заданные значения, объем выборки и нужную формулу для получения точечной оценки. Указание к шагу:
Вычисление
точечной оценки для среднего производится
по формуле: Вычисление смещенной точечной оценки для дисперсии производится по формуле:
- для выборки, заданной таблицей. Вычисление несмещенной точечной оценки для дисперсии производится по формуле:
2. Сосчитать значение оценки. |
Задание 2.1. Для случайно отобранных семи рабочих стаж работы оказался равным: 10,3,5,12,11,7,9. Чему равен для них средний стаж и чему равен разброс (среднеквадратическое отклонение)?
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Выписать заданные значения, объем выборки и нужную формулу для получения точечной оценки |
Задана выборка:
Формула для дисперсии
|
|
2 |
Сосчитать значение оценки |
|
Задание 2.2. При обследовании надоя коров случайным образом отобрали 307 коров, данные по ним сгруппировали и составили таблицу:
|
Надои |
3000-3400 |
3400-3800 |
3800-4200 |
4200-4800 |
4800-5000 |
|
Число коров |
43 |
71 |
102 |
64 |
27 |
Найти выборочное среднее, дисперсию и среднеквадратическое отклонение.

 - для выборки, заданной вариационным
рядом, и
- для выборки, заданной вариационным
рядом, и - для выборки, заданной таблицей.
- для выборки, заданной таблицей. - для выборки,
заданной вариационным рядом, и по
формуле:
- для выборки,
заданной вариационным рядом, и по
формуле:

 -формула
для среднего
-формула
для среднего -
-