
- •Теория вероятностей и математическая статистика
- •1. Вычисление вероятности события по классической формуле .
- •2. Вычисление вероятности событий по известным вероятностям других событий, с ними связанных.
- •3. Вычисление вероятности события по формуле полной вероятности
- •4. Построение многоугольника распределения дискретной случайной величины по ее ряду распределения
- •5. Вычисление вероятности попадания случайных величин х подчиненной нормальному законуна заданный интервал
- •1.Решения задач, когда все элементарные события равновероятны:.
- •Решение
- •2. Подсчет геометрических вероятностей:
- •Решение
- •3. Вероятности, связанные с подсчетом числа перестановок:
- •Решение
- •4. Вероятности, связанные с подсчетом числа размещений: .
- •Решение
- •5. Вероятности, связанные с подсчетом числа сочетаний:
- •Решение
- •6. Независимые события .
- •Решение
- •7. Формула полной вероятности:
- •Решение
- •8. Формула Байеса:
- •Решение
- •9. Математическое ожидание , дисперсия, стандартное отклонениедискретной случайной величины.
- •Найти математическое ожидание , дисперсию ,, вероятности .
- •Решение
- •13. Математическое ожидание , дисперсия,стандартное отклонение, вероятностиравномерного распределения.
- •Решение
- •Решение
- •Решение
- •2. Вычисление точечных оценок параметров распределения по выборке
- •Решение
- •Решение
- •3. Вычисление доверительных интервалов для среднего
- •Решение
- •4. Вычисление доверительного интервала для вероятности наступления событияс помощью таблиц нормального распределения.
- •Решение
- •Решение
- •5. Проверка статистических гипотез
- •Решение
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Записывается
функция плотности
|
|
|
2 |
Вычисляется
|
|
|
3 |
Вычисляется
|
|
13. Математическое ожидание , дисперсия,стандартное отклонение, вероятностиравномерного распределения.
|
Умения |
Алгоритм действий |
|
Математическое ожидание
|
1. Выписывается
функция распределения 2. Подсчитывается математическое ожидание
3. Подсчитывается дисперсия
4. Подсчитывается
стандартное отклонение
5.
Подсчитывается
|
Задание
13. Случайная величина
![]() –
время ожидания дождя в сутках - имеет
равномерное распределение на отрезке
–
время ожидания дождя в сутках - имеет
равномерное распределение на отрезке
![]() .
Найти математическое ожидание
.
Найти математическое ожидание
![]() ,
дисперсию
,
дисперсию![]() ,
вероятности
,
вероятности
![]() .
.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Записывается
функция плотности
|
|
|
2 |
Вычисляется математическое ожидание |
|
|
3 |
Вычисляется |
|
|
4 |
Вычисляется |
|
14.
Расчет наработки на отказ
![]() и вероятности
и вероятности
![]() .
.
|
Умения |
Алгоритм действий |
|
Расчет
наработки на отказ
|
1. Определяется
значение параметра
2.
Определяется наработка на отказ
|
Задание
14. Вероятность безотказной работы
прибора в течение
![]() часов равна
часов равна![]() .
.![]() -
момент отказа прибора. Найти математическое
ожидание
-
момент отказа прибора. Найти математическое
ожидание![]() - среднюю наработку на отказ
- среднюю наработку на отказ
![]() и вероятность безотказной работы прибора
в течение 500 ч.
и вероятность безотказной работы прибора
в течение 500 ч.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Записывается
функция плотности
|
|
|
2 |
Записывается
функция распределения
|
|
|
3 |
Вычисляется математическое ожидание. |
|
|
4 |
Вычисляется
|
|
15.
Нормальное распределение. Правило трех
сигм
![]() .
Правило двух сигм
.
Правило двух сигм
![]() .
.
Правило
одной сигмы
![]() .
.
|
Умения |
Алгоритм действий |
|
Нормальное распределение. Правило трех сигм:
Правило двух сигм:
Правило одной сигмы:
|
1. Определяются
значение параметров
2.Значения
3.Значения
4.Подсчитывается вероятности с помощью правил трех сигм, двух сигм и одной сигмы. |
Задание
15. Случайная величина
![]() имеет нормальное распределение
имеет нормальное распределение![]() ;
;![]() -
среднеквадратическое отклонение
-
среднеквадратическое отклонение
![]() .
Найти
.
Найти

Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Записывается
|
|
|
2 |
Вычисляется
|
|
|
3 |
Вычисляется
|
|
|
4 |
Вычисляется
|
|
|
5 |
Вычисляется
|
|
|
6 |
Вычисляется
|
|
16.
Неравенство Чебышева

|
Умения |
Алгоритм действий |
|
Неравенство Чебышева
|
1.Определяются
2.Значения
|
Задание 16. Все мужчины – случайная величина со средним 80 кг и дисперсией 50 кг2. Оценить с помощью неравенства Чебышева вероятность того, что вес случайно встреченного мужчины отличается от среднего на величину большую 10 кг.
Решение![]()
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Записываются
|
|
|
2 |
Подставляются
значения
|
Из неравенства Чебышева следует
|
17. Предельная формула Пуассона для последовательности независимых испытаний Бернулли.
|
Умения |
Алгоритм действий |
|
Предельная формула Пуассона для последовательности независимых испытаний Бернулли. |
1.Подсчитывается
значение
Если
|
Задание 17. Вероятность детали быть бракованной равна 0, 01. Произведено 300 деталей. Какова вероятность того, что в этой партии точно 4 бракованные детали? Более 4?
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Вычисляется
произведение
|
|
|
2 |
Подставляется
значение
|
|
18. Предельная интегральная теорема Муавра-Лапласа для последовательности независимых испытаний Бернулли.
|
Умения |
Алгоритм действий |
|
Предельная интегральная теорема Муавра-Лапласа для последовательности независимых испытаний Бернулли. |
1.Подсчитывается
значение
Если
2.Значения
|
Задание 18. Игральную кость бросают 600 раз. Какова вероятность того, что число выпадений шестерки будет между 90 и 105?
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Вычисляется
произведение
|
|
|
2 |
Вычисляется
значение
|
|
|
3 |
Вычисляются
значения
|
|
|
4 |
Значения
|
|
Теория вероятностей и математическая статистика.
1. Построение по выборке таблицы распределения, полигона и гистограммы.
|
Умения |
Алгоритм действий |
|
Построение по выборке таблицы распределения, полигона и гистограммы |
1. Упорядочить заданные значения по возрастанию, сосчитать их количество. 2. Если надо, сгруппировать значения; сосчитать число значений, попавших в интервалы разбиения; вычислить эмпирические частоты; составить таблицу эмпирического распределения. 3. По таблице эмпирического распределения нарисовать гистограмму и полигон, найти медиану. |
Задание 1.Построить гистограмму и полигон по заданной таблице: Распределение семей по размеру жилой площади, приходящейся на одного человека (цифры условные).
|
№/п |
Площадь, приходящаяся на одного человека |
Число семей с данным размером площади |
|
1 |
3-5 |
10 |
|
2 |
5-7 |
20 |
|
3 |
7-9 |
40 |
|
4 |
9-11 |
30 |
|
5 |
11-13 |
15 |
|
|
Всего |
115 |


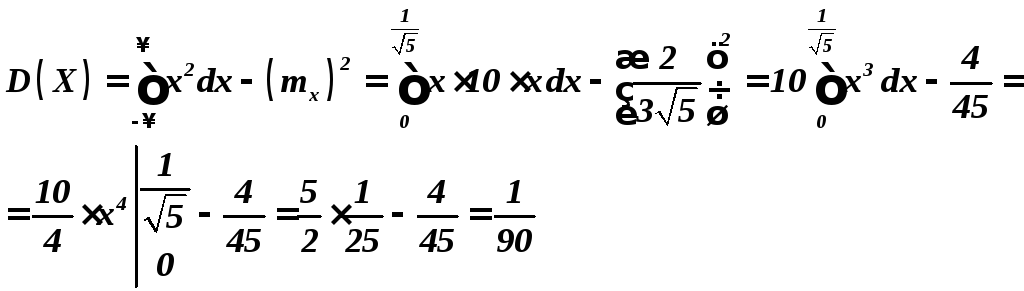

 .
.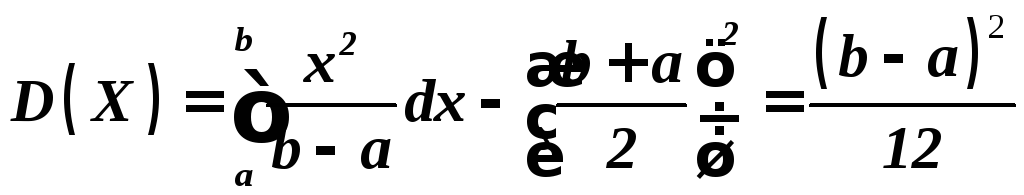


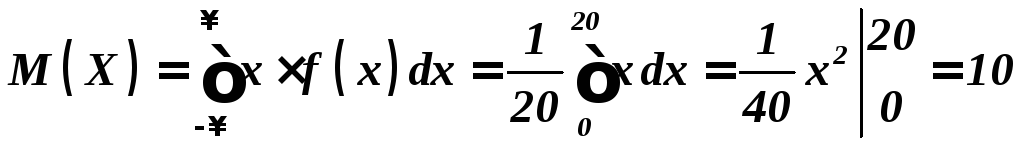






 и
и берутся из таблицы нормального
распределения.
берутся из таблицы нормального
распределения.







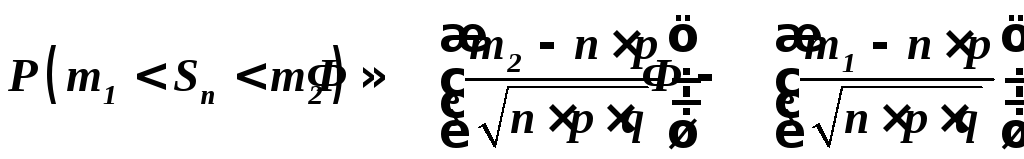
 находятся из таблиц нормального
распределения.
находятся из таблиц нормального
распределения.

