- •Теория вероятностей и математическая статистика
- •1. Вычисление вероятности события по классической формуле .
- •2. Вычисление вероятности событий по известным вероятностям других событий, с ними связанных.
- •3. Вычисление вероятности события по формуле полной вероятности
- •4. Построение многоугольника распределения дискретной случайной величины по ее ряду распределения
- •5. Вычисление вероятности попадания случайных величин х подчиненной нормальному законуна заданный интервал
- •1.Решения задач, когда все элементарные события равновероятны:.
- •Решение
- •2. Подсчет геометрических вероятностей:
- •Решение
- •3. Вероятности, связанные с подсчетом числа перестановок:
- •Решение
- •4. Вероятности, связанные с подсчетом числа размещений: .
- •Решение
- •5. Вероятности, связанные с подсчетом числа сочетаний:
- •Решение
- •6. Независимые события .
- •Решение
- •7. Формула полной вероятности:
- •Решение
- •8. Формула Байеса:
- •Решение
- •9. Математическое ожидание , дисперсия, стандартное отклонениедискретной случайной величины.
- •Найти математическое ожидание , дисперсию ,, вероятности .
- •Решение
- •13. Математическое ожидание , дисперсия,стандартное отклонение, вероятностиравномерного распределения.
- •Решение
- •Решение
- •Решение
- •2. Вычисление точечных оценок параметров распределения по выборке
- •Решение
- •Решение
- •3. Вычисление доверительных интервалов для среднего
- •Решение
- •4. Вычисление доверительного интервала для вероятности наступления событияс помощью таблиц нормального распределения.
- •Решение
- •Решение
- •5. Проверка статистических гипотез
- •Решение
8. Формула Байеса:
|
Умения |
Алгоритм действий |
|
Формула Байеса:
|
1.Выделяется
полная группа событий
2. Подсчитываются
условные вероятности
3.
Значения
|
Задание 8. 15% всех мужчин и 5% всех женщин – дальтоники. Наугад выбранное лицо оказалось дальтоником. Какова вероятность того, что это мужчина. Число мужчин и женщин считается одинаковым.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Выделяется
полная группа событий
|
|
|
2 |
Вычисляются
условные вероятности
|
|
|
3 |
Значения
|
|
9. Математическое ожидание , дисперсия, стандартное отклонениедискретной случайной величины.
|
Умения |
Алгоритм действий |
|
Математическое
ожидание
|
1. Составляется таблица распределения дискретной случайной величины.
2. Подсчитываются
математическое ожидание
3. Подсчитывается
дисперсия
4.
Подсчитывается стандартное отклонение
|
Задание
9. Случайная величина
![]() задана
рядом распределения:
задана
рядом распределения:
|
|
-3 |
0 |
1 |
4 |
|
|
0,1 |
0,3 |
0,4 |
0,2 |
|
|
9 |
0 |
1 |
16 |
Найти математическое ожидание , дисперсию ,, вероятности .
Найти
математическое ожидание
![]() ,
дисперсию
,
дисперсию![]() ,
,![]() .
.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Вычисляется
математическое ожидание
|
|
|
2 |
Вычисляется
дисперсия
|
|
|
3 |
Вычисляются
|
|
|
4 |
Вычисляются
|
|
10.
Биномиальное распределение:
![]()
|
Умения |
Алгоритм действий |
|
Биномиальное
распределение: |
1.Подсчитываются
нужные биномиальные коэффициенты 2.Значения
|
Задание
10. Футболист бьёт 5 раз пенальти.
Вероятность, забить при одном ударе –
0,8. какова вероятность того, что будет
забито ровно 3 мяча? Более 2? Найти
математическое ожидание
![]() ,
дисперсию
,
дисперсию
![]() .
.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Записываются
значения
|
|
|
2 |
Вычисляются
|
|
|
3 |
Вычисляется
математическое ожидание
|
|
|
4 |
Вычисляется
дисперсия
|
|
11.
Распределение Пуассона:
![]()
|
Умения |
Алгоритм действий |
|
Распределение Пуассона:
|
1. Определяется
значение параметра
2.Вероятности
|
Задание
11. Количество
![]() принимаемых за час звонков по домашнему
телефону имеет распределение Пуассона.
Среднее количество принимаемых за час
звонков
принимаемых за час звонков по домашнему
телефону имеет распределение Пуассона.
Среднее количество принимаемых за час
звонков![]() .
Какова вероятность того, что будет
принято за час точно 3 звонка? Более 2
звонков?
.
Какова вероятность того, что будет
принято за час точно 3 звонка? Более 2
звонков?
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие данной ситуации предложенному алгоритму |
|
1 |
Записывают
значения
|
|
|
2 |
Вычисляется
или берется из табл. 1
|
|
|
3 |
Вычисляется
или определяется с помощью табл. 2
|
|
12.
Математическое ожидание
![]() ,
дисперсия
,
дисперсия![]() ,
стандартное отклонение
,
стандартное отклонение![]() ,
вероятности
,
вероятности![]() непрерывной случайной величины.
непрерывной случайной величины.
|
Умения |
Алгоритм действий |
|
Математическое
ожидание
|
1. Выписывается
функция распределения
2. Подсчитывается
математическое ожидание
3. Подсчитывается
дисперсия
4. Подсчитывается
стандартное отклонение
5. Подсчитывается
|
Задание
12. Функция плотности случайной величины
![]() имеет вид:
имеет вид:
Найти
математическое ожидание
![]() ,
дисперсию
,
дисперсию
![]() ,
,
![]()


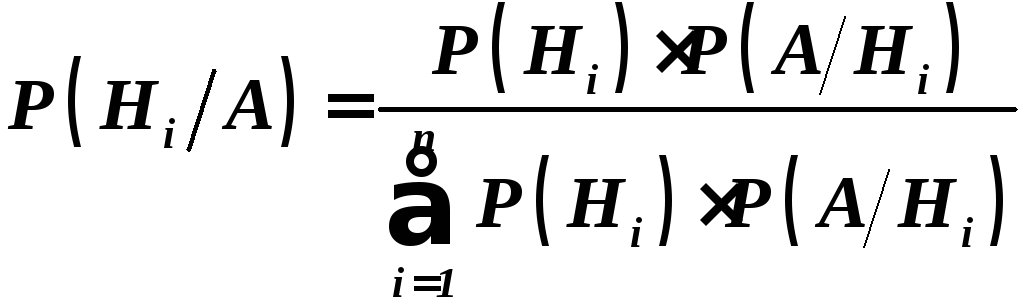



 .
.
 и
и