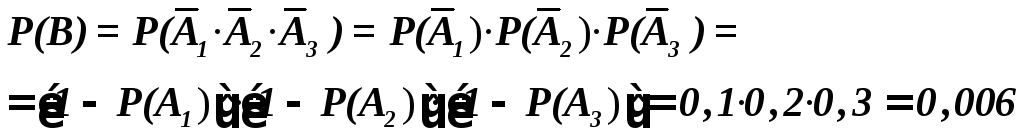Теория вероятностей и математическая статистика
1. Вычисление вероятности события по классической формуле .
|
№ п/п |
Умения |
Алгоритм действий |
|
1 |
Вычисление
вероятности события
|
1. Дать описание
стохастического эксперимента, в
результате которого может произойти
событие
2.Вычислить
общее число
3.Вычислить
число исходов
4.Вычислить
вероятность события
|
по классической формуле
.
исходов данного стохастического
эксперимента.
,
благоприятствующих событию
.
.
Задание 1. Студент знает ответ на 30 вопросов из 50. Какова вероятность ответить правильно на билет, состоящий из 3 вопросов?
Решение
|
№ п/п |
Алгоритм действий |
Конкретное соответствие задания предложенному алгоритму |
|
1. |
Дать
описание стохастического эксперимента,
в результате которого может произойти
событие
|
Студент вытаскивает билет, состоящий из трех вопросов.
|
|
2. |
Вычислить
общее число
|
|
|
3. |
Вычислить
число исходов
|
|
|
4. |
Вычислить вероятность события
|
|
исходов данного стохастического
эксперимента
-
число способов выбрать три вопроса
из исходных.
,
благоприятствующих событию
-
число способов выбрать три вопроса
из 30 известных студенту.
2. Вычисление вероятности событий по известным вероятностям других событий, с ними связанных.
|
№ п/п |
Умения |
Алгоритмы |
|
1 |
Вычисление вероятности событий по известным вероятностям других событий, с ними связанных. |
1.Обозначить все события, указанные в задаче, и известные вероятности. 2.Установить связи между событиями. 3.Используя теоремы сложения и умножения вероятностей, а также формулу для вычисления противоположного события, вероятности. |
Задание 2. Стрелок производит 3 выстрела по мишени. Вероятности попадания при первом, втором и третьем выстрелах соответственно равны 0,9;0,8 и 0,7. Найти вероятности того, что в результате этих выстрелов окажется
а) ни одного попадания;
б) хотя бы одно попадание;
в) ровно одно попадание;
г) ровно три попадания.
Считать, что выстрелы производятся независимо друг от друга.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие задания предложенному алгоритму |
|
1. |
Обозначить все события, указанные в задаче, и известные вероятности |
B - ни одного попадания C - хотя бы одно попадание D - ровно одно попадание E - ровно три попадания |
|
2. |
Установить связи между событиями |
|
|
3. |
Используя теоремы сложения и умножения вероятностей, а также формулу для вычисления противоположного события, вычислить требуемые вероятности. |
|
-
попал при 1-м выстреле;
-
попал при 2-м выстреле;
-
попал при 3-м выстреле;
3. Вычисление вероятности события по формуле полной вероятности
|
№ п/п |
Алгоритм действий |
|
1 |
Дать
описание всех гипотез |
|
2 |
Вычислить
вероятности каждой гипотезы
|
|
3 |
Вычислить
условную вероятность события А при
каждой гипотезе |
|
4 |
Вычислить
вероятность событий А:
|
,
на которые можно разбить пространство
элементарных исходов и события А.
.
,
вычислив их.
Задание 3. Специалист высшей квалификации собирает 40% приборов, надежность которых равна 0,95 приборов, надежность которых равна 0,75. Определить вероятность того, что случайно отобранный прибор будет работать безотказно.
Решение
|
№ п/п |
Алгоритм |
Конкретное соответствие задания предложенному алгоритму |
|
1. |
Дать
описание всех гипотез, на которые
можно разбить пространство элементарных
исходов и события
|
|
|
2. |
Вычислить вероятности каждой гипотезы |
|
|
3. |
Вычислить
условную вероятность события
|
|
|
4. |
Вычислить
вероятность события
|
|
.
-
прибор собран специалистом высшей
квалификации
-
прибор собран специалистом средней
квалификации
-
прибор работает безотказно.
при каждой гипотезе
по формуле полной вероятности