
- •Министерство образования и науки Российской Федерации Государственное образовательное учреждение высшего профессионального образования "поволжский государственный университет сервиса (пвгус)"
- •Учебно-методический комплекс дисциплины
- •Содержание
- •Введение
- •Рабочая учебная программа дисциплины
- •1.1. Цели и задачи дисциплины
- •1.2.Структура и объем дисциплины
- •1.3. Содержание дисциплины Распределение фонда времени по темам и видам занятий
- •1.4. Требования к уровню освоения дисциплины и формы текущего и промежуточного контроля
- •Перечень вопросов для подготовки к зачету по дисциплине «Информатика»
- •1.5. Содержание индивидуальной работы студента (под руководством преподавателя)
- •2. Учебно-методическое пособие
- •2.1. Конспект лекций
- •Тема 1. Информация и информационные процессы
- •1.1. Системы, образованные взаимодействующими элементами, состояния элементов, обмен информацией между элементами, сигналы
- •1.2 Меры и единицы представления, измерения и хранения информации
- •Синтаксическая мера информации
- •Семантическая мера информации
- •Прагматическая мера информации
- •Единицы измерения информации.
- •1.3 Системы счисления
- •Формы представления чисел
- •Двоичная система счисления
- •Правила выполнения простейших арифметических действий.
- •1.4. Основные понятия алгебры логики. Логические основы эвм.
- •Тема 2. Информационные модели и системы
- •2.1. Информационная модель объекта
- •2.2. Алгоритм и его свойства. Структура алгоритма.
- •Тема 3.Средства и технологии создания и преобразования информационных объектов
- •3.1. Текстовые процессоры
- •3.2. Электронные таблицы
- •3.3. Базы данных
- •Виды моделей данных
- •Классификация баз данных
- •Реляционные базы данных
- •Основные понятия реляционных баз данных
- •3.4. Графические редакторы
- •Тема 4. Компьютер как средство автоматизации информационных процессов
- •4.1. История развития эвм. Понятие и основные виды архитектуры эвм
- •4.2. Состав и назначение основных элементов персонального компьютера. Центральный процессор. Системные шины и слоты расширения
- •4.3. Запоминающие устройства: классификация, принцип работы, основные характеристики
- •4.4. Устройства ввода/вывода данных, их разновидности и основные характеристики
- •4.5. Классификация программного обеспечения. Виды программного обеспечения и их характеристики.
- •4.6. Системное программное обеспечение.
- •4.7. Защита информации.
- •Вредоносные программы
- •Классификация антивирусных программ
- •Тема 5. Средства и технологии обмена информацией с помощью компьютерных сетей (сетевые технологии)
- •5.1. Локальные компьютерныесети.
- •5.2. Базовые сетевые топологии
- •5.3. Сетевое оборудование
- •5.4. Глобальные сети эвм.
- •История
- •Адресация в Интернете
- •5.5. Поисковые информационные системы
- •Тема 6. Основы социальной информатики.
- •2.3. Лабораторный практикум по дисциплине Распределение тем лабораторных занятий по времени
- •Содержание лабораторных занятий лабораторная работа №1. « кодирование информации»
- •Кодирование символьной информации
- •Кодирование графических изображений
- •Лабораторная работа №2. «информация и энтропия»
- •Лабораторная работа №3. «позиционные системы счисления»
- •Краткие теоретические сведения:
- •Формы представления чисел
- •Двоичная система счисления
- •Восьмеричная и шестнадцатеричная системы счисления
- •Взаимное преобразование двоичных, восьмеричных и шестнадцатеричных чисел
- •Двоично-десятичная система счисления
- •Лабораторная работа №4. «проектирование алгоритмов. Блок-схема алгоритма»
- •Лабораторная работа №5. «основные приемы работы в microsoft word»
- •Интересное предложение
- •Образец формул
- •Лабораторная работа №6. «Технология создания электронных таблиц в ms Excel»
- •Функции ms Excel
- •Задания для выполнения:
- •Лабораторная работа №7. «основы обработки реляционных баз данных средствами
- •1. 2. Задания для самостоятельной работы
- •Лабораторная работа №8. «Логические основы функционирование эвм»
- •Логические элементы
- •Лабораторная работа №9. «Основы работы с MathCad»
- •Лабораторная работа №10. «информационная безопасность. Основы криптографии»
- •Тулыио целзио тсдизло
- •Современные алгоритмы шифрования
- •Лабораторная работа №11. «Создание одноранговой сети»
- •Требования к оформлению и защите лабораторных работ
- •3. Учебно-методическое обеспечение дисциплины
- •3.1. Перечень основной и дополнительной литературы
- •3.2 Методические рекомендации для преподавателя
- •3.3. Методические указания студентам по изучению дисциплины
- •3.4. Методические указания для выполнения кОнтрольной работы
- •Варианты заданий для выполнения контрольной работы
- •3.5. Материально-техническое и программное обеспечение дисциплины
- •3.6. Программное обеспечение
- •Поволжский государственный университет сервиса
- •Поволжский государственный университет сервиса
- •Приложение 1
1.4. Основные понятия алгебры логики. Логические основы эвм.
При записи тех или иных логических выражений используется специальный язык, который принят в математической логике. Основоположником математической логики является великий немецкий математик Готфрид Вильгельм Лейбниц(1646 - 1716 гг.). Он сделал попытку построить универсальный язык, с помощью которого споры между людьми можно было бы разрешать посредством вычислений. На заложенном Лейбницем фундаменте ирландский математикДжордж Бульпостроил здание новой науки - математической логики, - которая в отличие от обычной алгебры оперирует не числами, а высказываниями. В честь Д.Буля логические переменные в языке программирования Паскаль впоследствии назвалибулевскими.
Высказывание- это любое утверждение, относительно которого можно сказать истинно оно или ложно, т.е. соответствует оно действительности или нет. Таким образом по своей сути высказывания фактически являются двоичными объектами и поэтому часто истинному значению высказывания ставят в соответствие 1, а ложному - 0. Например, запись А = 1 означает, что высказывание А истинно.
Высказывания могут быть простымиисложными. Простые соответствуют алгебраическим переменным, а сложные являются аналогом алгебраических функций. Функции могут получаться путем объединения переменных с помощью логических действий.
Самой простой логической операцией
является операция НЕ(по-другому
ее часто называютотрицанием,дополнением или инверсиейи обозначаютNOTX или![]() .
Результат отрицания всегда противоположен
значению аргумента.
.
Результат отрицания всегда противоположен
значению аргумента.
Логическая операция НЕ является унарной, т.е. имеет всего один операнд. В отличие от нее, операции И (AND) и ИЛИ (OR) являются бинарными, так как представляют собой результаты действий над двумя логическими величинами.
Операцию НЕ можно задать в виде таблицы
|
X |
|
|
0 |
1 |
|
1 |
0 |
Логическое Иеще часто называютконъюнкцией, илилогическим умножением.
Операция И имеет результат «истина» только в том случае, если оба ее операнда истинны. Принято обозначать значком «&»либо «^»
Например, рассмотрим высказывание «Для остановки ОС «Windows'95» требуется процессор не ниже 80386 и не менее 4 Мбайт оперативной памяти». Из него следует, что установка будет успешной только при одновременном выполнении обоих условий: даже если у вас в машинеPentium, но мало ОЗУ (равно как и при 8 Мбайт ОЗУ процессор 80286), «Windows'95» работать откажется.
|
X |
Y |
XY |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Операция ИЛИ -дизъюнкцией,
илилогическим сложением. Она дает
«истину», если значение «истина» имеет
хотя бы один из операндов. Принято
обозначать значком «![]() »либо
«+». Разумеется, в случае, когда справедливы
оба аргумента одновременно, результат
по-прежнему истинный. Действительно,
когда студентка просит друга подарить
ей на день рождения букет цветов или
пригласить в кафе, можно без опасении
сделать и то, и другое одновременно
(впрочем, на практике в таком случае
можно ограничиться чем-то одним).
»либо
«+». Разумеется, в случае, когда справедливы
оба аргумента одновременно, результат
по-прежнему истинный. Действительно,
когда студентка просит друга подарить
ей на день рождения букет цветов или
пригласить в кафе, можно без опасении
сделать и то, и другое одновременно
(впрочем, на практике в таком случае
можно ограничиться чем-то одним).
|
X
|
Y
|
X
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
Приведенные выше таблицы значений переменных для логических операций называются таблицами истинности. В них указываются все возможные комбинации логических переменных Х и Y, а также соответствующие им результаты операций. Таблица истинности может рассматриваться в качестве одного из способов задания логической функции.
Операции И, ИЛИ, НЕ образуют полную систему логических операций, из которой можно построить сколь угодно сложное логическое выражение.
В вычислительной технике также часто используется операция исключающее ИЛИ (XOR), которая отличается от обыкновенного ИЛИ только при Х=1 иY=l.
Как видно из табл. 1.2, операция XORфактически сравнивает на совпадение два двоичных разряда. Хотя теоретически основными базовыми логическими операциями всегда называют именно И, ИЛИ, НЕ, на практике по технологическим причинам в качествеосновного логического элементаиспользуется элементИ-НЕ(последняя колонка в табл. 1.2).
Таблица 1.2. Дополнительные логические операции
|
Х
|
Y
|
X XORY
|
NOT(XANDY)
|
|
0
|
0
|
0
|
1
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
0
|
Можно проверить, что на базе элементов И-НЕ могут быть скомпонованы все базовые логические элементы (И, ИЛИ, НЕ), а значит и любые другие, более сложные.
Для упрощения логических выражений используют законы алгебры логики.
Таблица 1.3. Законы алгебры логики
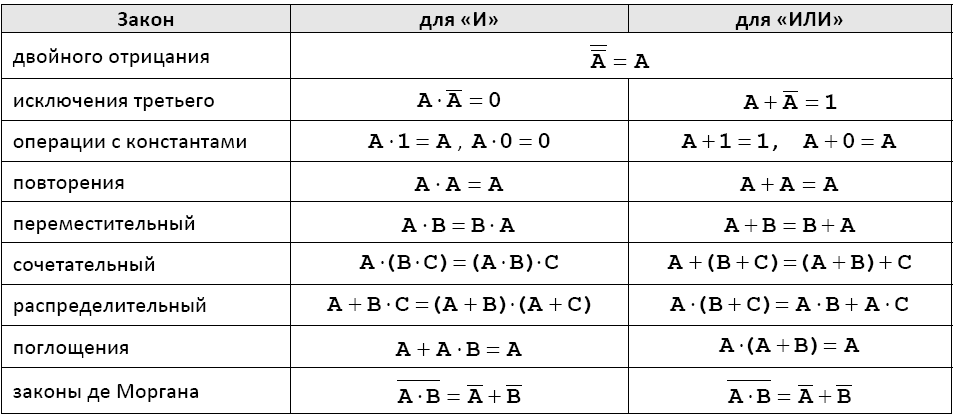
В компьютерах все вычисления выполняются с помощью логических элементов–электронных схем, выполняющих логические операции. Обозначения простейших элементов приводиться в таблице (ГОСТ 2.743-91). Обратите внимания, что небольшойкружок на выходе обозначает операцию НЕ(инверсию).

Если нужно составить схему по известному логическому выражению, ее начинают строить с конца. Находят операцию, которая будет выполняться последней, и ставят на выходе соответствующий логический элемент. Затем повторяют то же самое для сигналов, поступающих на вход этого элемента. В конце концов, должны остаться только исходные сигналы –переменные в логическом выражении.
Составим схему, соответствующую выражению
![]()

Добавляем элемент И:

Ставим элемент НЕ:

Аналогично разбираем вторую ветку:

Схема составлена, ее входами являются сигналы А, В и С, а выходом Х.
