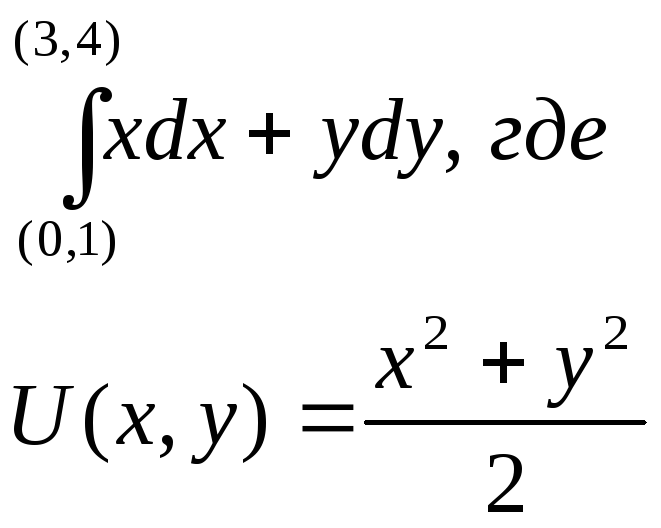Математика 2( русс.) 2 сем ПС,СТР,БЖЗО,ТМО,ПСМ
.doc
|
№ |
Уровень сложности |
Вопросы |
Тема |
Ответ A |
Ответ B |
Ответ C |
Ответ D |
Ответ E |
|
|
2 |
Найти частные
производные функции
|
1 |
|
|
|
|
|
|
|
2 |
Частная
производная первого порядка по
переменной х (
|
1 |
|
|
|
|
|
|
|
2 |
Частная
производная первого порядка по
переменной у (
|
1 |
|
|
|
|
|
|
|
2 |
Частная
производная первого порядка по
переменной х ( |
1 |
|
|
|
|
|
|
|
2 |
Частная
производная первого порядка по
переменной у ( |
1 |
|
|
|
|
|
|
|
1 |
Найти частные
производные функции
|
1 |
|
|
|
|
|
|
|
1 |
Частная
производная первого порядка по
переменной
|
1 |
|
|
|
|
0 |
|
|
1 |
Частная производная первого порядка
по переменной у (
|
1 |
-2у+2 |
|
|
|
|
|
|
1 |
Частная
производная первого порядка по
переменной
|
1 |
2х+2 |
|
|
|
0 |
|
|
1 |
Частная производная первого порядка по переменной
|
1 |
|
|
|
|
0 |
|
|
1 |
Частная
производная первого порядка по
переменной
|
1 |
10х-7 |
24х+24-7 |
24х |
24y |
0 |
|
|
1 |
Частная
производная первого порядка по
переменной
функции
|
1 |
9 |
2x |
2x+y |
2y |
X2+9 |
|
|
1 |
Найти
частные производные функции
|
1 |
|
|
|
|
|
|
|
2 |
Частная
производная первого порядка по
переменной
|
1 |
|
|
|
|
|
|
|
2 |
Частная
производная первого порядка по
переменной
функции
|
1 |
|
|
|
|
|
|
|
2 |
Найти
частные производные функции
|
1 |
|
|
|
|
|
|
|
2 |
Найти
частные производные функции
|
1 |
|
|
|
|
|
|
|
2 |
Найти
проекции градиента
|
1 |
|
|
|
|
|
|
|
1 |
Найти
проекции градиента
|
1 |
{9x2-7; 8y3+1} |
|
{9x2;8y3+1} |
{9x2 ; 8y3} |
{9x2-7; 8y3} |
|
|
1 |
Найти проекции
градиента
|
1 |
{3; -10y+7} |
{3; -24} |
{3х; -24y+7} |
{3х; -24y} |
{3; -24y-7} |
|
|
2 |
|
1 |
{-2;1} |
{-4;5} |
{-3;-4} |
{-1;4} |
{-2;4} |
|
|
2 |
|
1 |
{3,-1} |
{-4;5} |
{-2;1} |
{-3;-4} |
{-2;4} |
|
|
2 |
|
1 |
{4,4} |
{-2;1} |
{-3;-4} |
{-4;5} |
{-2;4} |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
1 |
Найти
производную функции
|
1 |
|
|
|
|
|
|
|
1 |
Найти
производную функции
|
1 |
0 |
1 |
-1 |
2 |
-2 |
|
|
1 |
Найти производную функции
|
1 |
- |
|
|
5 |
6 |
|
|
1 |
Какую замену надо использовать для решения однородного дифференциального уравнения первого порядка? |
2 |
|
|
|
|
|
|
|
1 |
Чтобы
понизить порядок дифференциального
уравнения
|
2 |
|
|
|
|
|
|
|
1 |
Укажите
общее решение однородного линейного
уравнения, соответствующего уравнению
|
2 |
|
|
|
|
|
|
|
1 |
Чтобы
понизить порядок дифференциального
уравнения
|
2 |
|
|
|
|
|
|
|
1 |
Найдите
частное решение дифференциального
уравнения
|
2 |
|
|
|
|
|
|
|
1 |
Какие из следующих дифференциальных уравнений первого порядка являются линейными: А)
|
2 |
А), Б), В) |
Б) |
В) |
А),Б) |
А),В) |
|
|
1 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
2 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
1 |
Решить дифференциальное
уравнение:
|
2 |
|
|
|
|
|
|
|
1 |
При каком значении
к функция
|
2 |
2 |
0 |
1 |
|
|
|
|
2 |
При каком значении
к функция
|
2 |
|
6 |
3 |
-3 |
|
|
|
1 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
2 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
2 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
2 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
3 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
2 |
Решить
дифференциальное уравнение:
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
1 |
2 |
0 |
3 |
5 |
|
|
3 |
Уравнение
|
2 |
Уравнение с разделяющимися переменными |
Дифференциальное уравнение в полных дифференциалах |
Уравнение Бернулли |
Квадратичным уравнением |
Уравнение Клеро |
|
|
2 |
|
2 |
однородное |
Дифференциальное уравнение с разделяющимися переменными |
Дифференциальное уравнение в полных дифференциалах |
Уравнение Бернулли |
линейное |
|
|
1 |
Определите
тип дифференциального уравнения
|
2 |
однородное |
Дифференциальное уравнение с разделяющимися переменными |
Дифференциальное уравнение в полных дифференциалах |
Уравнение Бернулли |
линейное |
|
|
1 |
Определите
тип дифференциального уравнения
|
2 |
однородное |
Дифференциальное уравнение с разделяющимися переменными |
Дифференциальное уравнение в полных дифференциалах |
Уравнение Бернулли |
линейное |
|
|
1 |
Определите
тип дифференциального уравнения |
2 |
линейное |
Дифференциальное уравнение с разделяющимися переменными |
Дифференциальное уравнение в полных дифференциалах |
Уравнение Бернулли |
Лагранжа |
|
|
2 |
Составить линейное однородное дифференциальное уравнение зная его фундаментальную систему решений
|
2 |
|
|
|
|
|
|
|
2 |
Составить линейное однородное дифференциальное уравнение зная его фундаментальную систему решений
|
2 |
|
|
|
|
|
|
|
1 |
Определить
степень однородности функции
|
2 |
2 |
1 |
0 |
3 |
|
|
|
1 |
Определить
степень однородности функции |
2 |
3 |
2 |
1 |
0 |
4 |
|
|
1 |
Определить
степень однородности функции |
2 |
0 |
1 |
2 |
-1 |
4 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
Решить
дифференциальное уравнение
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение
|
2 |
|
|
|
|
|
|
|
1 |
Решить
дифференциальное уравнение
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
1 |
Как определяется площадь плоской фигуры с помощью двойного интеграла? |
3 |
|
|
dxdydz |
x=0,y=0,z=0 |
|
|
|
2 |
Переход к полярной системе координат в двойном интеграле |
3 |
|
|
|
|
|
|
|
2 |
Как определяется объем тела с помощью двойного интеграла?
|
3 |
|
dxdydz |
|
|
|
|
|
1 |
Геометрический
смысл интеграла
|
3 |
|
|
|
|
|
|
|
1 |
|
3 |
8 |
1 |
4 |
5 |
2 |
|
|
1 |
|
3 |
|
3 |
4 |
8 |
10 |
|
|
2 |
|
3 |
|
5 |
2 |
8 |
1 |
|
|
1 |
|
3 |
|
5 |
2 |
8 |
1 |
|
|
2 |
|
3 |
1 |
|
5 |
2 |
8 |
|
|
2 |
|
3 |
|
8 |
1 |
4 |
5 |
|
|
1 |
|
3 |
|
|
3 |
4 |
8 |
|
|
1 |
|
3 |
ln2 |
1 |
|
|
|
|
|
1 |
|
3 |
|
5 |
2 |
8 |
1 |
|
|
1 |
|
3 |
|
1.5 |
2.3 |
5 |
1.1 |
|
|
1 |
|
3 |
|
5 |
9 |
11 |
17 |
|
|
1 |
|
3 |
9 |
1/9 |
1/80 |
1/4 |
1/7 |
|
|
1 |
|
3 |
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
2 |
|
3 |
0 |
|
-3 |
-7 |
1/5 |
|
|
2 |
|
3 |
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
1 |
|
3 |
9 |
0 |
-3 |
-7 |
1/5 |
|
|
2 |
D:
|
3 |
|
5 |
2 |
7 |
0 |
|
|
2 |
|
3 |
20 |
-10 |
0 |
1 |
-20 |
|
|
2 |
D:
|
3 |
8 |
-4 |
0 |
7/8 |
-9 |
|
|
3 |
|
3 |
|
|
|
|
|
|
|
3 |
|
3 |
|
e |
e-2 |
e2 |
e2-e-1 |
|
|
2 |
Изменить порядок интегрирования
|
3 |
|
|
|
|
|
|
|
2 |
Изменить порядок интегрирования
|
3 |
|
|
|
|
|
|
|
3 |
Изменить порядок интегрирования
|
3 |
|
|
|
|
|
|
|
3 |
Расставить
пределы интеграла:
|
3 |
|
|
|
|
|
|
|
3 |
Расставить
пределы интеграла
|
3 |
|
|
|
|
|
|
|
2 |
|
3 |
|
|
0 |
2 |
-1 |
|
|
2 |
|
3 |
|
1 |
3 |
2 |
4 |
|
|
3 |
|
3 |
|
|
0 |
2 |
-1 |
|
|
3 |
|
3 |
|
- |
|
|
100 |
|
|
3 |
Вычислить:
D: y=x, y=x2 |
3 |
|
6 |
-6 |
5 |
-5 |
|
|
3 |
|
3 |
|
|
- |
0 |
|
|
|
3 |
|
3 |
|
|
|
- |
0 |
|
|
3 |
|
3 |
|
|
|
|
|
|
|
3 |
D: І – четверть круга, где R=1, центр в точке (0,0) |
3 |
|
|
|
|
0 |
|
|
3 |
D: круг, где центр в точке О(0;0) с радиусом r |
3 |
|
|
|
|
|
|
|
2 |
Как выражаются точки М(x,y,z) в цилиндрической системе координат? |
3 |
x= |
x= |
x= |
x= |
x=
|
|
|
2 |
Как определяется объем тела с помощью тройного интеграла? |
3 |
|
|
|
|
|
|
|
2 |
Как выражаются точки М(x,y,z) в сферической системе координат? |
3 |
x= |
x= |
x= |
x= |
x= |
|
|
1 |
Геометрический
смысл интеграла
|
3 |
|
|
|
S |
Момент инерции |
|
|
2 |
Элемент объема в цилиндрической системе координат |
3 |
dV= |
dV= |
dV=4 |
dV= |
dV= |
|
|
2 |
Элемент объема в сферической системе координат. |
3 |
dV= |
dV= |
dV= |
dV= |
dV= |
|
|
2 |
Как определяется обьем тела с помощью тройного интеграла. |
3 |
|
|
|
|
|
|
|
1 |
Геометрический смысл
интеграла
|
3 |
Обьем тела |
Масса тела |
Площадь фигуры |
Момент инерции |
Координаты центра тяжести пластинки |
|
|
1 |
|
4 |
4 |
-1/5 |
4/9 |
1,8 |
9/10 |
|
|
1 |
|
4 |
|
-1/5 |
4/9 |
1,8 |
9/10 |
|
|
3 |
T: |
4 |
|
15 |
4,8 |
1/78 |
114 |
|
|
1 |
|
4 |
|
|
|
|
|
|
|
1 |
|
4 |
2 |
3 |
1 |
4 |
5 |
|
|
2 |
|
4 |
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
1 |
|
|
1 |
|
4 |
3 |
|
|
|
|
|
|
1 |
|
4 |
|
25 |
75 |
27 |
81 |
|
|
1 |
|
4 |
|
75 |
27 |
81 |
0 |
|
|
1 |
|
4 |
|
|
|
|
|
|
|
1 |
|
4 |
6 abc |
|
|
|
|
|
|
1 |
|
4 |
48 |
|
|
|
|
|
|
1 |
|
4 |
abc |
8 |
92 |
105 |
94 |
|
|
2 |
|
4 |
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
1 |
|
|
2 |
|
4 |
16 |
8 |
4 |
|
|
|
|
1 |
|
4 |
6 |
2 |
4 |
5 |
3 |
|
|
1 |
|
4 |
|
|
|
|
|
|
|
1 |
|
4 |
|
|
|
|
|
|
|
1 |
|
4 |
|
|
|
|
|
|
|
1 |
|
4 |
2 |
1 |
3 |
4 |
5 |
|
|
2 |
|
4 |
|
|
|
|
|
|
|
2 |
|
4 |
|
4 |
5,8 |
9,2 |
1,7 |
|
|
2 |
|
4 |
1 |
|
|
|
|
|
|
2 |
|
4 |
4 |
|
|
|
|
|
|
1 |
Расставить пределы
интегрирования в тройном интеграле
|
4 |
|
|
|
|
|
|
|
2 |
Расставить пределы
интегрирования
|
4 |
|
|
|
|
|
|
|
1 |
Расставить пределы
интегрирования в тройном интеграле
|
4 |
|
|
|
|
|
|
|
3 |
|
4 |
|
|
0 |
1 |
- |
|
|
3 |
Переходя к сферическим
координатам вычислить
|
4 |
|
|
1 |
|
|
|
|
3 |
Криволинейный интеграл
второго рода (вычисление в декартовой
системе координат):
|
5 |
|
|
|
|
|
|
|
3 |
Длина дуги L на плоскости ХОУ |
5 |
|
|
|
|
|
|
|
3 |
|
5 |
|
1 |
|
0 |
2 |
|
|
2 |
|
5 |
1/3 |
2 |
1 |
0 |
3 |
|
|
1 |
|
5 |
2/3 |
0 |
1/3 |
2 |
3 |
|
|
3 |
|
5 |
-1 |
|
4 |
0 |
3 |
|
|
1 |
|
5 |
1 |
0 |
4 |
3 |
1/2 |
|
|
1 |
|
5 |
1 |
11 |
0 |
-1/2 |
-2/3 |
|
|
1 |
|
5 |
1 |
1/2 |
-1/2 |
0 |
3 |
|
|
1 |
|
5 |
1 |
4 |
2 |
3 |
-2 |
|
|
1 |
|
5 |
0 |
1 |
2 |
5 |
8/9 |
|
|
1 |
|
5 |
-9/2 |
4/5 |
6/8 |
0 |
3 |
|
|
1 |
|
5 |
1/2 |
1/6 |
1 |
0 |
2 |
|
|
3 |
Как
вычисляется криволинейный интеграл
первого рода
|
5 |
|
|
|
|
|
|
|
3 |
Формула Грина |
5 |
|
|
|
|
|
|
|
3 |
Условие независимости криволинейноого интеграла от пути интегрирования. |
5 |
|
|
|
|
|
|
|
3 |
Как определяется работа при движении точки в силовом поле? |
5 |
|
|
|
|
|
|
|
3 |
Какое силовое поле называется потенциальным? |
5 |
|
|
|
|
|
|
|
3 |
|
5 |
|
|
|
1 |
|
|
|
1 |
|
5 |
|
10 |
5 |
4 |
1 |
|
|
1 |
|
5 |
|
|
|
|
|
|
|
1 |
|
5 |
0 |
1 |
2 |
3 |
4 |
|
|
1 |
|
5 |
|
|
|
|
0 |
|
|
2 |
|
5 |
|
|
|
|
1 |
|
|
2 |
|
5 |
|
10 |
5 |
0 |
7 |
|
|
1 |
|
5 |
0 |
1 |
2 |
3 |
4 |
|
|
1 |
|
5 |
|
|
|
|
|
|
|
1 |
|
5 |
|
|
|
|
|
|
|
1 |
|
5 |
0 |
|
|
|
|
|
|
3 |
Найти массу четверти
окружности х2+у2=1,
расположенной в первом квадранте если
плотность
|
5 |
|
0 |
1 |
2 |
3 |
|
|
3 |
Дивергенция векторного поля
|
6 |
|
|
|
|
0 |
|
|
2 |
Определить поверхности уровня скалярного поля
|
6 |
сферы |
цилиндры |
конусы |
параллелепипеды |
параболоиды |
|
|
2 |
Определить поверхности уровня скалярного поля
|
6 |
конусы |
цилиндры |
сферы |
окружности |
параболоиды |
|
|
3 |
Вычислить поверхность
куба
|
6 |
3а4 |
|
10 |
|
|
|
|
3 |
|
6 |
|
|
|
0 |
1 |
|
|
3 |
|
6 |
0 |
1 |
6а |
3а2 |
6а3 |
|
|
3 |
По формуле Стокса преобразовать интеграл
|
6 |
|
|
|
|
|
|
|
2 |
|
6 |
|
|
|
1 |
х2+у2 |
|
|
2 |
|
6 |
|
|
|
|
|
|
|
2 |
Применяя формулу Грина преобразовать интеграл
|
6 |
|
|
|
|
|
|
|
2 |
|
6 |
3 |
1/4 |
2/5 |
1 |
9 |
|
|
1 |
АВ-прямая |
6 |
0 |
1/4 |
2/5 |
1 |
9 |
|
|
1 |
|
6 |
8 |
2 |
9 |
7 |
3 |
|
|
1 |
|
6 |
4 |
2 |
8 |
3 |
5 |
|
|
1 |
|
6 |
2/3 |
1/4 |
2/5 |
1 |
9 |
|
|
2 |
Вычислить интеграл от полного дифференциала
|
6 |
|
2/3 |
1/4 |
2/5 |
1 |
|
|
1 |
|
6 |
|
58 |
-12 |
56 |
14 |
|
|
1 |
|
6 |
|
6 |
1 |
9 |
7 |
|
|
1 |
|
6 |
8 |
2 |
3 |
4 |
9 |
|
|
1 |
|
6 |
8 |
0 |
1 |
-4 |
2,4 |
|
|
1 |
|
6 |
12 |
|
4 |
|
1 |
|
|
3 |
|
6 |
|
|
4 |
|
1 |
|
|
1 |
|
6 |
|
|
3 |
1/5 |
2 |
|
|
2 |
Преобразовать по
формуле Грина
|
6 |
|
|
|
|
|
|
|
1 |
Преобразовать по
формуле Грина |
6 |
|
|
|
|
|
|
|
1 |
|
6 |
|
|
10 |
11/12 |
5 |
|
|
1 |
|
6 |
|
5 |
2 |
3 |
-2 |
|
|
1 |
L-окружность
|
6 |
|
0 |
|
|
|
|
|
1 |
Площадь фигуры через криволинейный интеграл |
6 |
|
|
|
|
|
|
|
3 |
Что называется интегралом по поверхности второго рода |
6 |
|
|
|
|
|
|
|
2 |
Как определяется
нормаль
|
6 |
|
|
|
|
|
|
|
2 |
Как определяют
направляющие косинусы
нормали |
6 |
|
|
|
|
|
|
|
2 |
Чему
равняется
|
6 |
|
|
|
|
|
|
|
2 |
Чему
равняется
|
6 |
|
|
|
|
|
|
|
2 |
Чему
равняется
|
6 |
|
|
|
|
|
|
|
2 |
Формула Остроградского-Гаусса |
6 |
|
|
|
|
|
|
|
2 |
Что
называется дивергенцией вектора
|
6 |
|
|
|
|
|
|
|
1 |
Как вычисляется
|
6 |
|
|
|
|
|
|
|
2 |
Какое
поле |
6 |
|
|
|
|
|
|
|
2 |
Что означает
|
6 |
Поле свободно от источников и стоков |
Существует источник |
Поле свободно от источников |
Существует сток |
Существует и сток, и источник |
|
|
2 |
Что означает
|
6 |
Существует сток |
Существует источник |
Поле свободно от источников и стоков |
Существует и сток, и источник |
Поле свободно от источников |
|
|
2 |
Что означает
|
6 |
Существует источник |
Существует сток |
Поле свободно от источников и стоков |
Существует и сток, и источник |
Поле потенциально |
|
|
2 |
Чему
равняется поток ротора
|
6 |
Циркуляции
вектора
|
|
|
|
|
|
|
2 |
Какое поле называется потенциальным? |
6 |
Если
|
Если
|
Если
|
Если
|
Если
|
|
|
1 |
Чему
равняется
|
6 |
0 |
1 |
-1 |
2 |
|
|
|
2 |
Найти
градиент скалярного поля
|
6 |
|
|
|
0 |
1 |
|
|
2 |
Найти
дивергенцию векторного поля
|
6 |
1 |
0 |
6 |
3 |
7 |
|
|
2 |
Найти
дивергенцию вектора
|
6 |
0 |
5 |
-1 |
1 |
|
|
|
2 |
Найти
|
6 |
0 |
5 |
-2 |
-1 |
|
|
|
3 |
Найти
|
6 |
5ху |
0 |
1 |
2ху |
5 |
|
|
3 |
|
6 |
|
|
4/3 |
4 |
3 |
|
|
2 |
|
6 |
|
|
0 |
1 |
3xy+C |
|
|
2 |
|
6 |
2 |
1 |
0 |
3 |
4 |
|
|
2 |
Найти
|
6 |
0 |
-1 |
2 |
3 |
(1,1,1) |
|
|
2 |
Найти
|
6 |
6 |
-6 |
2 |
3 |
(0,0) |
|
|
2 |
Найти
|
6 |
0 |
6 |
2 |
3 |
(1,1,1) |
|
|
2 |
Дивергенция
векторного поля
|
6 |
0 |
1 |
2 |
-1 |
(0,0) |
|
|
1 |
|
6 |
(0;0) |
1 |
(1,1) |
(0,1) |
(-1,-1) |
|
|
2 |
Найти
потенциал поля
|
6 |
|
0 |
1 |
-1 |
|
|
|
3 |
Общий член числового
ряда
|
7 |
|
|
|
|
|
|
|
3 |
Необходимое условие сходимости выполнено для ряда: |
7 |
|
|
|
|
|
|
|
3 |
Первые три члена
ряда
|
7 |
|
|
|
|
|
|
|
3 |
Общий член числового
ряда
|
7 |
|
|
|
|
|
|
|
3 |
Исследовать на сходимость по признаку Даламбера
|
7 |
Сходится |
условно сходится |
0 |
расходится |
абсолютно сходится |
|
|
2 |
Исследовать на сходимость по признаку Даламбера
|
7 |
Сходится |
абсолютно сходится |
расходится |
Сходится
при
|
условно сходится |
|
|
1 |
Вычислить первые
пять членов ряда
|
7 |
|
|
|
|
|
|
|
1 |
Вычислить первые
пять членов ряда
|
7 |
|
|
|
|
|
|
|
1 |
Вычислить первые
пять членов ряда
|
7 |
|
|
|
|
|
|
|
2 |
Исследовать на
сходимость по радикальному признаку
Коши
|
7 |
сходится |
абсолютно сходится |
расходится |
Сходится
при
|
условно сходится |
|
|
3 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
7 |
условно сходится |
абсолютно сходится |
расходится |
Сходится
при
|
сходится |
|
|
3 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
7 |
условно сходится |
Сходится
при
|
абсолютно сходится |
расходится |
сходится |
|
|
1 |
Под событием понимают такой результат эксперимента или наблюдения, который при реализации данного комплекса условий может: |
|
Произойти или не произойти |
Произойти |
не произойти |
Обязательно произойти |
Неизбежно произойти |
|
|
1 |
Какое событие называют достоверным? |
8 |
Которое неизбежно произойдет при определенном комплексе условий |
Которое не может произойти при определенном комплексе условий |
Которое может либо произойти, либо нет |
Это результат эксперимента… |
Любое событие |
|
|
1 |
Какое событие называют невозможным? |
8 |
Которое не может произойти при определенном комплексе условий |
Которое неизбежно произойдет при определенном комплексе условий |
Которое может либо произойти, либо нет |
Это результат эксперимента… |
Любое событие |
|
|
1 |
Какое событие называют случайным? |
8 |
Которое при испытании может либо произойти, либо нет |
Которое не может произойти при определенном комплексе условий |
Которое неизбежно произойдет при определенном комплексе условий |
Это результат эксперимента… |
Любое событие |
|
|
1 |
Укажите формулу классического определения вероятности |
8 |
Р(А)=m/n |
W(A)=m/n |
A |
C |
P |
|
|
1 |
Укажите формулу по которой вычисляется относительная частота |
8 |
W(A)=m/n |
Р(А)=m/n |
A |
C |
P |
|
|
1 |
Вероятность достоверного события равна: |
8 |
1 |
0 |
|
2 |
0,1 |
|
|
1 |
Вероятность невозможного события равна: |
8 |
0 |
1 |
|
2 |
0,1 |
|
|
1 |
Вероятность случайного события Р(А) удовлетворяет неравенствам…: |
8 |
|
|
|
|
|
|
|
1 |
Найдите формулу с помощью которой находятся перестановки из n различных элементов: |
8 |
P |
A |
C |
C |
P |
|
|
1 |
Найдите формулу с помощью которой находится число размещений из n элементов по k элементов : |
8 |
A |
C |
C |
P |
A |

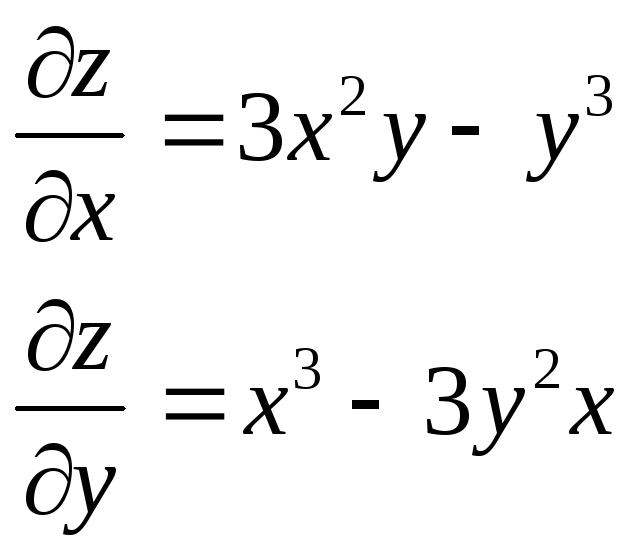

















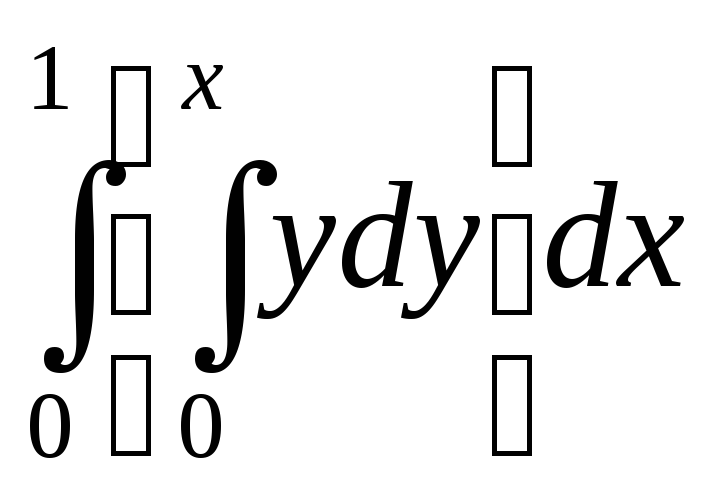







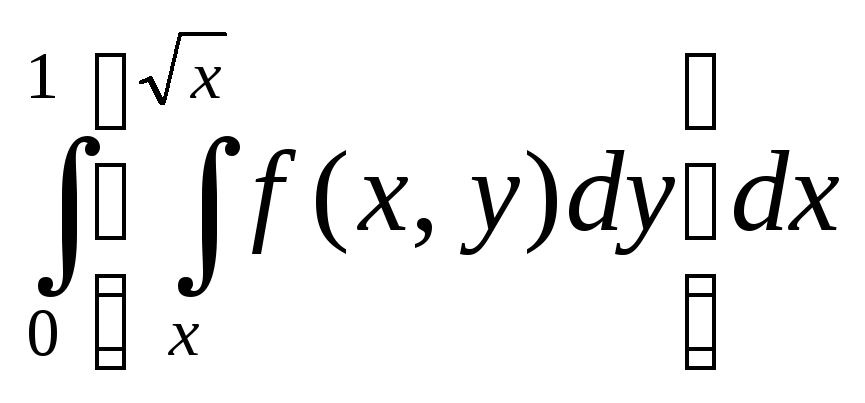

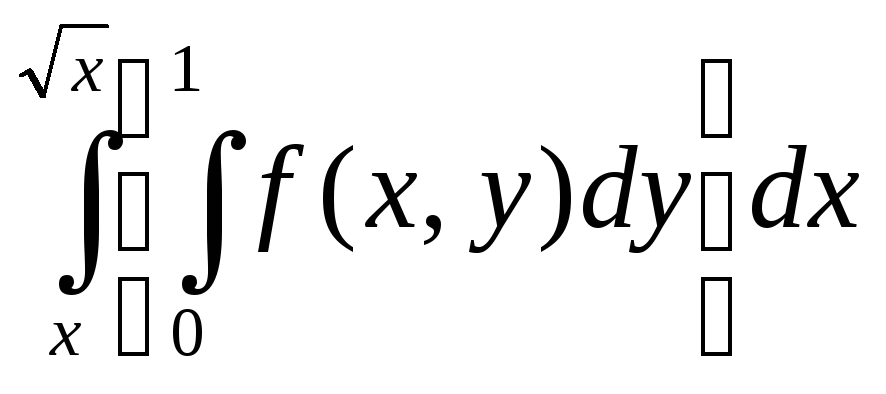




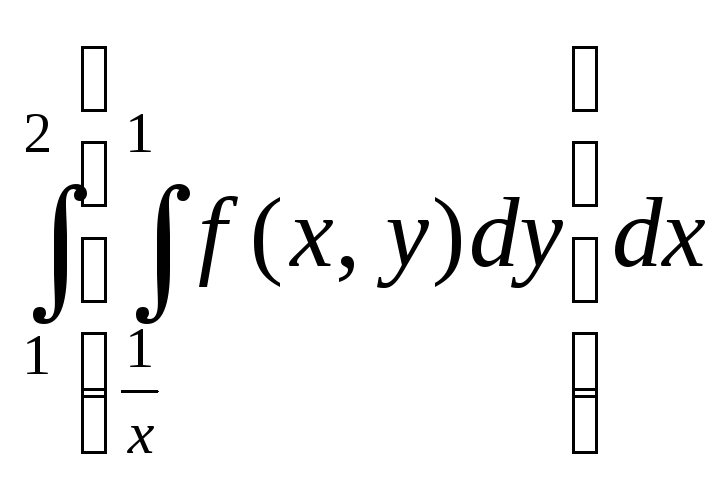







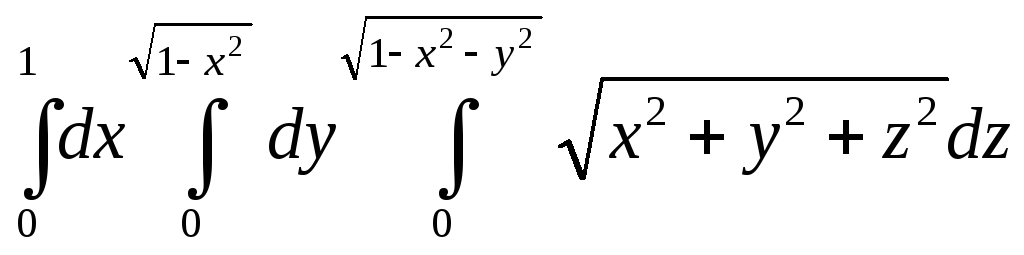







 по пути
по пути
 по
пути
по
пути
 по
пути
по
пути
 по пути
по пути
 по пути у=х-3
по пути у=х-3
 по пути
по пути
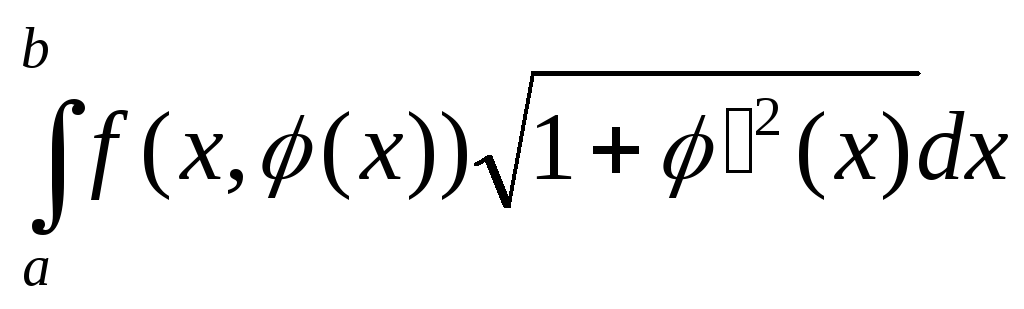
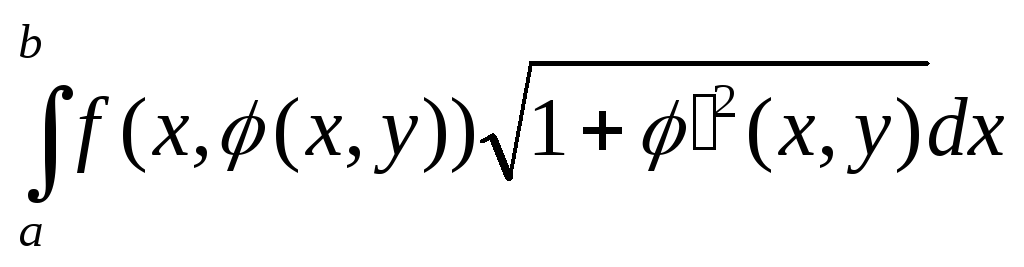
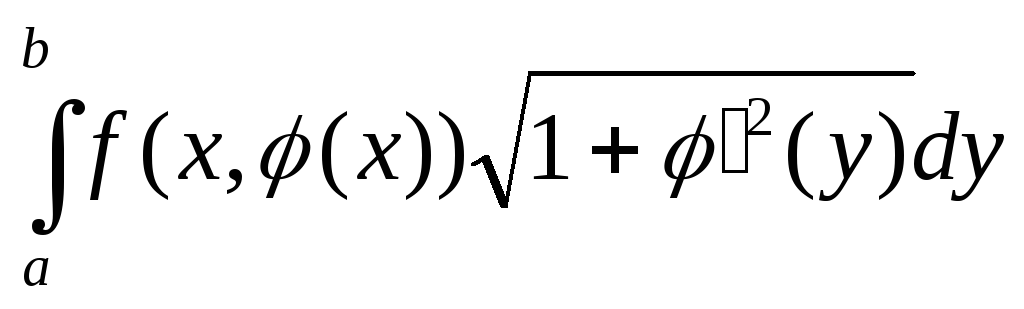


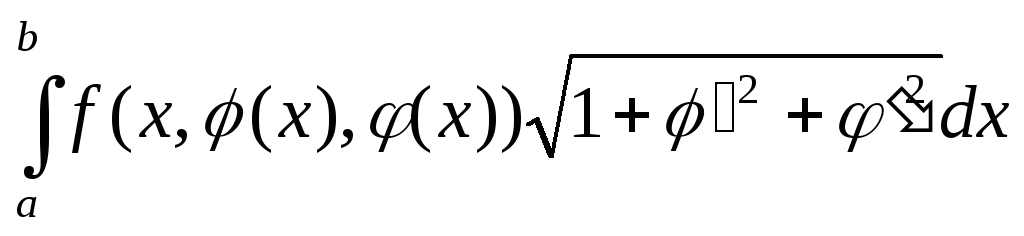


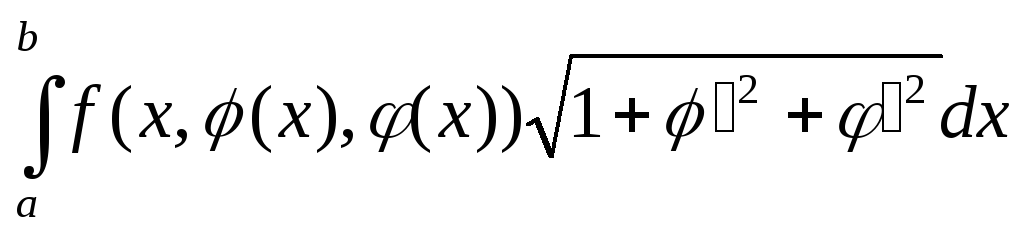
 -окружность
-окружность х=у
х=у -
окружность
-
окружность

 у=х3
у=х3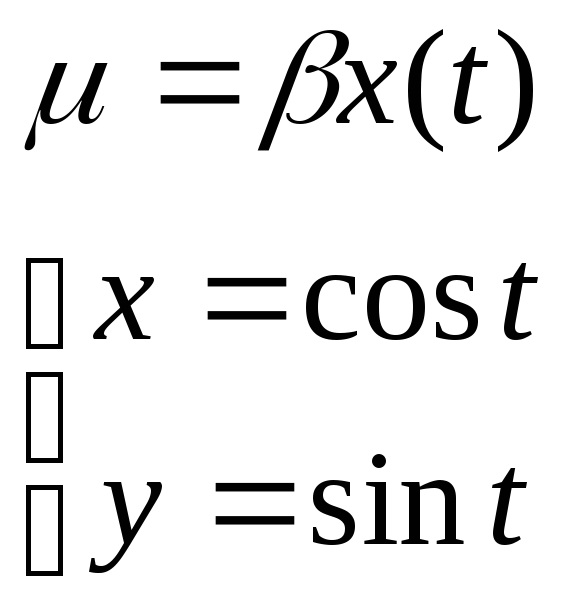






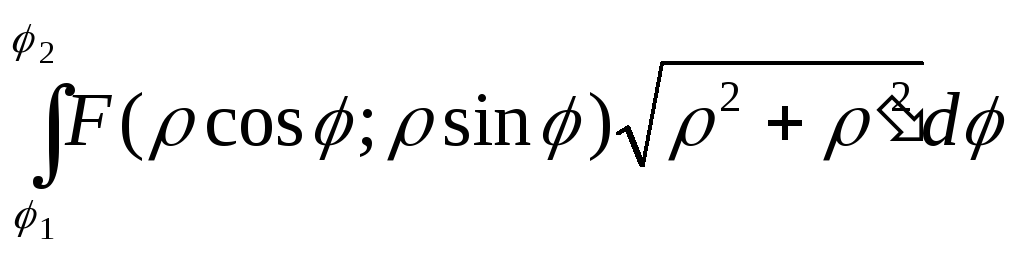




 U=xy
U=xy U=x2y
U=x2y y=x
y=x
 х=0
х=0
 ,
где U(x,y)=xy
,
где U(x,y)=xy