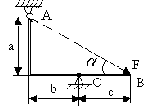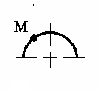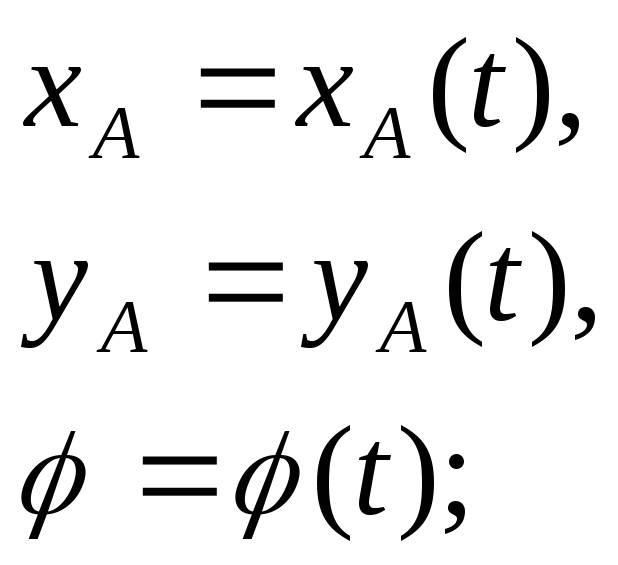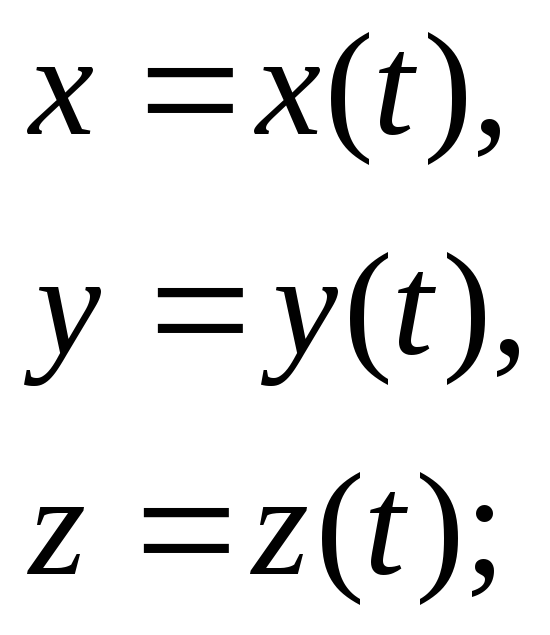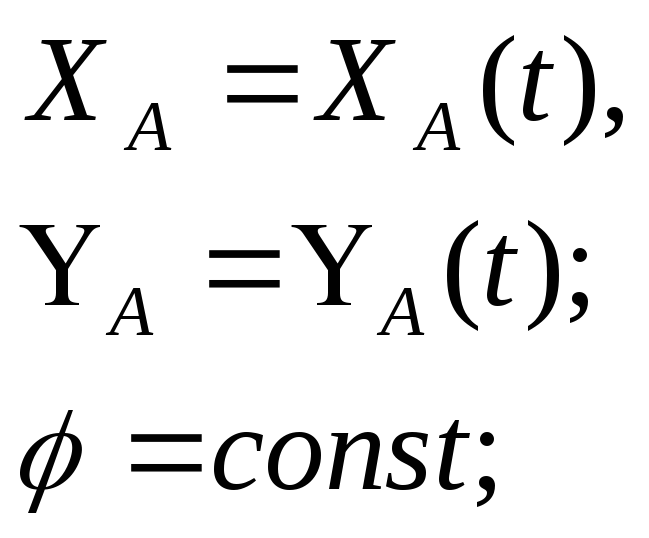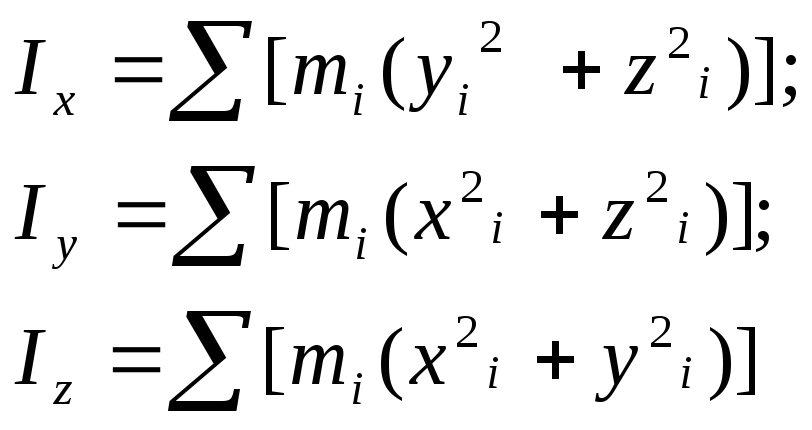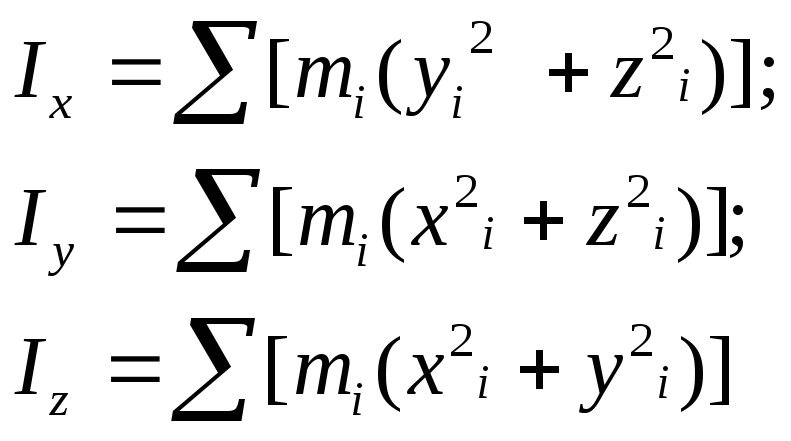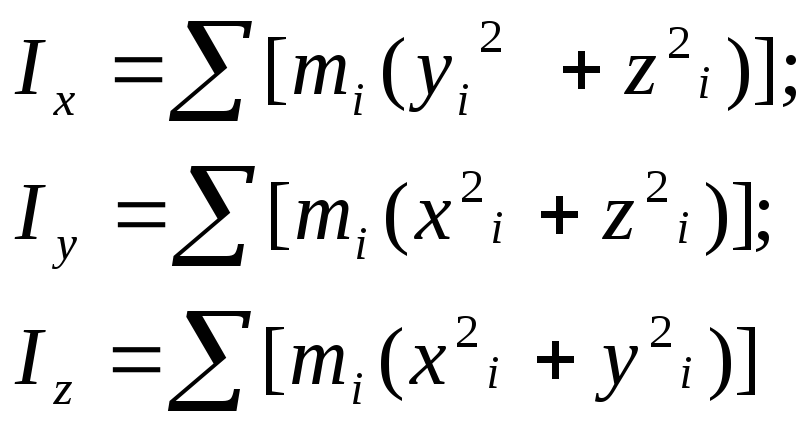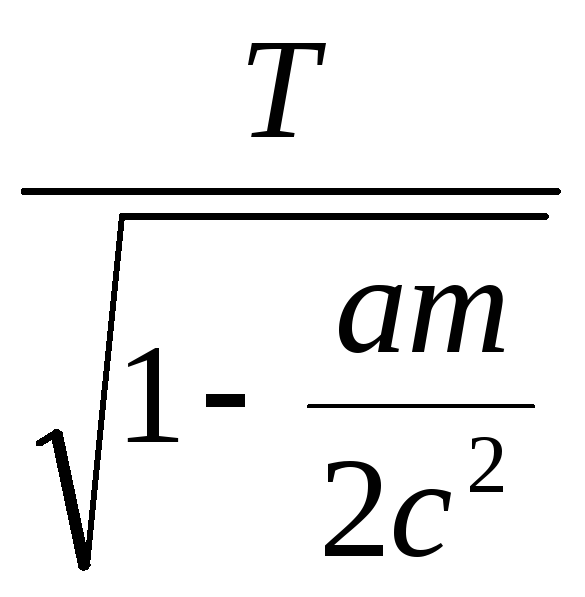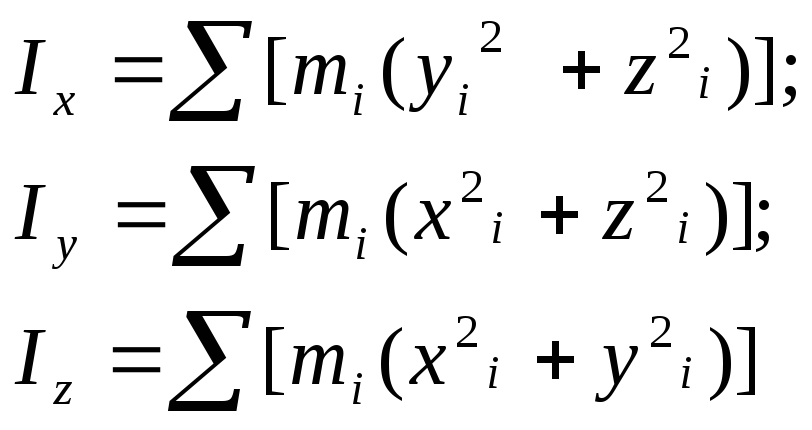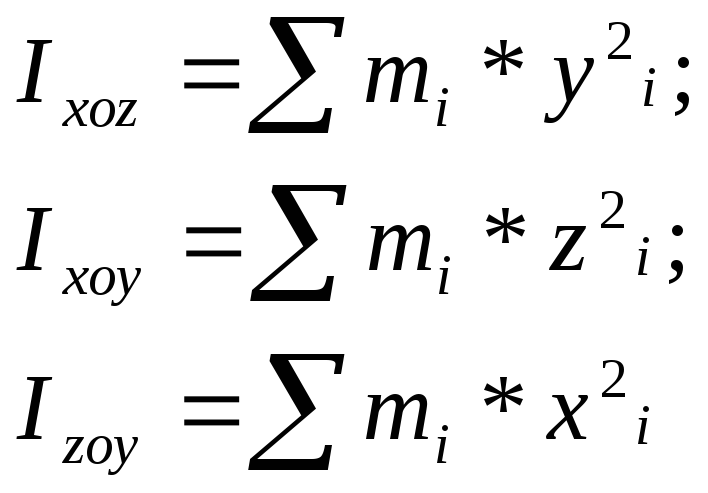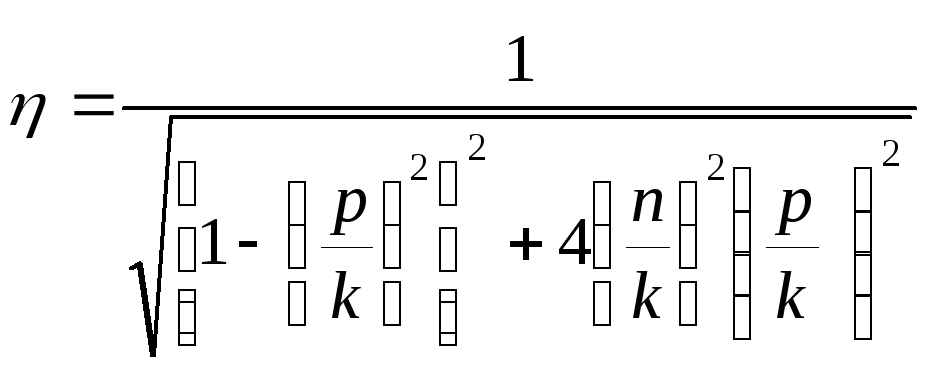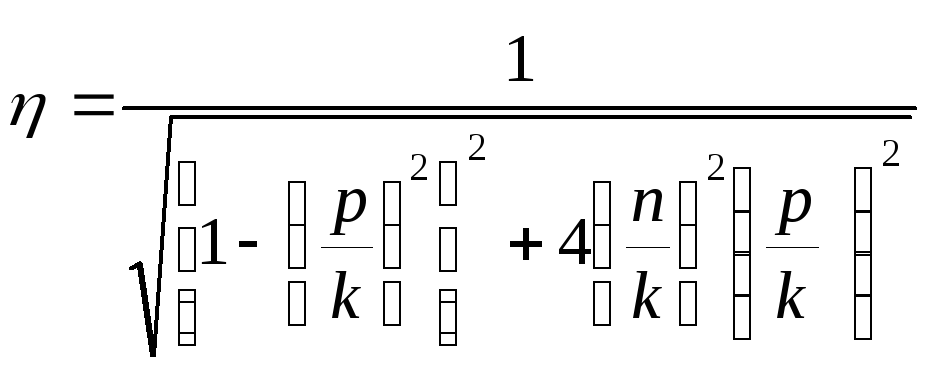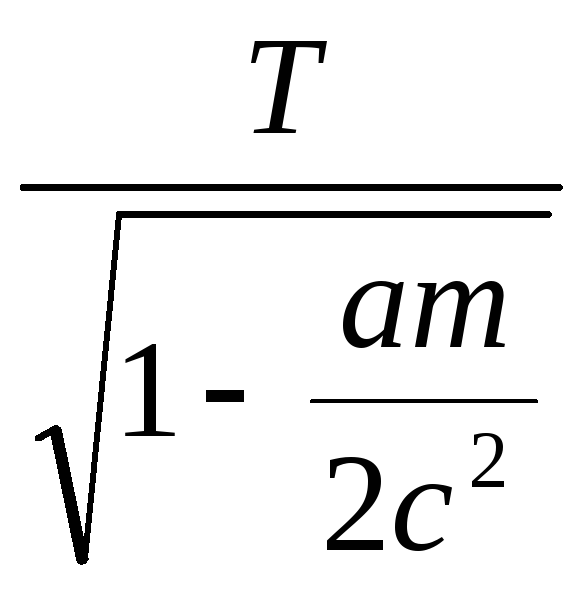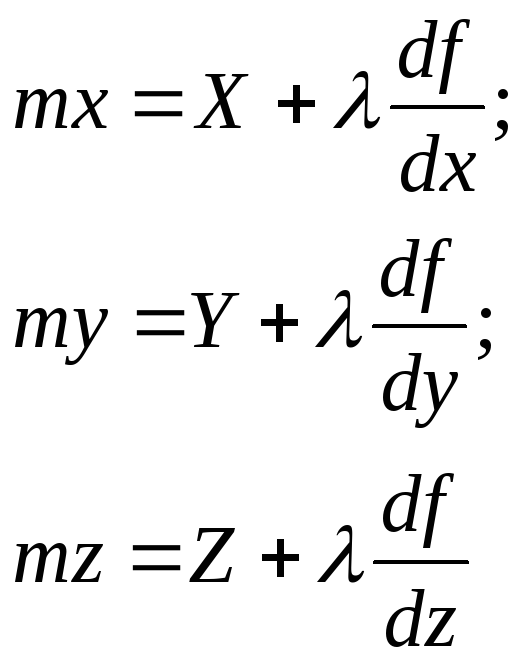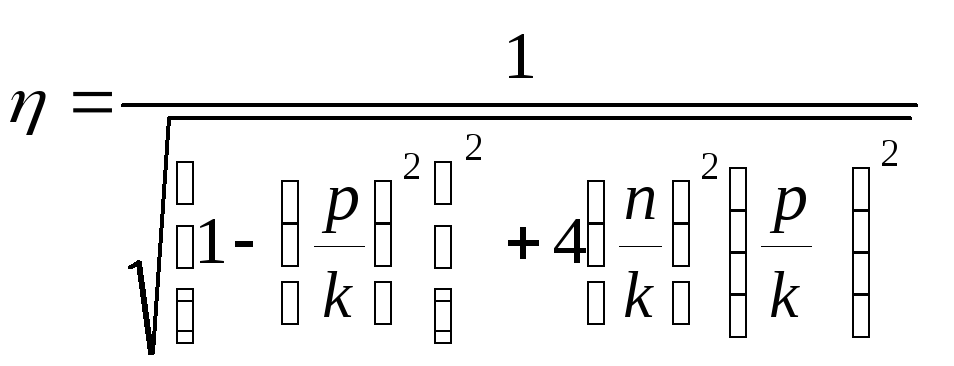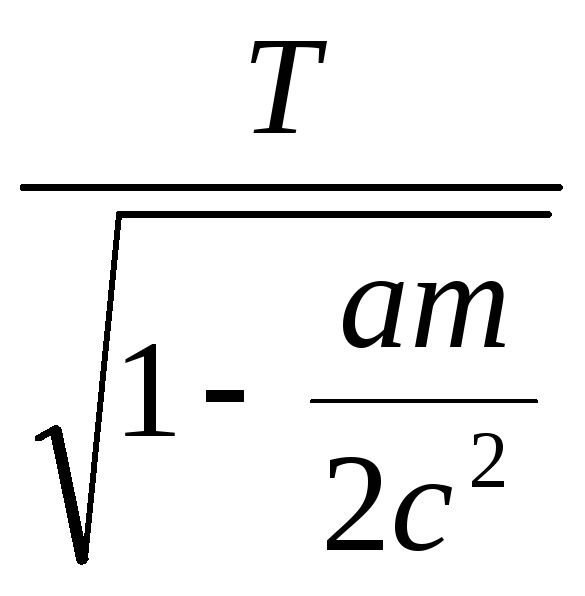Теоретическая Механика Сессия
.doc
3. Перечень экзаменационных вопросов и тестовых заданий
Тестовые вопросы по «Теоретической механике» на 2012-2013 учебный год.
Специальность 5B072400 – «Технологические машины и оборудование»,
5B071200– Машиностроение», 5B09 0100 - «Транспорт, транспортная техника и технологии»
Язык обучения – русский
1 курс семестр 2 группа ТМО-12, МС-12, ТТТ-12
Ответственный за разработку тестов – к.т.н., и.о. доцента Омарова Н.И.
|
№ |
Уровень сложности |
Вопрос |
Раздел, тема |
Ответ А
|
Ответ В |
Ответ С |
Ответ Д |
Ответ Е |
|
|
1 |
1 |
Какие тела абсолютно свободные? |
1.1 |
Которые могут совершать любые перемещения в пространстве. |
Которые вращаются |
Которые не деформируются |
Перемещения которых в каких-либо направлениях ограничены |
Которые могут перемещаться по горизонтали |
|
|
2 |
2 |
В каком случае две силы находятся в равновесии? |
1.2 |
Если они равны по модулю и действуют по одной линии действия в противоположные стороны |
Если они будут равны по модулю |
Если они противоположны по направлению |
Если они направлены по одной линии действия |
Если они действуют по одной линии действия в противоположные стороны |
|
|
3 |
2 |
Какие характерные точки имеет сила на чертеже? |
1.2 |
Начало и конец силы |
Начало силы |
Модуль силы |
Направление силы |
Линию дейс-твия силы
|
|
|
4 |
2 |
Какие системы сил являются эквивалентными? |
1.2 |
При замене одной системой сил другой системой – состояние тела не изменяется
|
Равные по модулю |
Уравновешенные |
Противоположные по направлению |
Направленные под углом 450 друг к другу |
|
|
5 |
2 |
Что значит сила – равнодействующая? |
1.2 |
Сила – эквивалентная системе сил |
Сила инерции |
Центробежная сила |
Уравновешивающая сила |
Реактивная сила |
|
|
6 |
2 |
Чему равна уравновешивающая сила? |
1.2 |
Равная по модулю равнодействующей но направлена в противоположную сторону по линии действия |
Сумме всех сил, действующих на тело |
Разности сил, действующих на тело |
Равна равнодействующей и направлена в ту же сторону |
Диагонали параллелограмма построенного на этих силах |
|
|
7 |
2 |
Измениться ли состояние тела если к нему добавить или отнять уравновешенную систему сил? |
1.2 |
Согласно 3 аксиоме статики – нет |
Согласно закону динамики – измениться |
Тело будет двигаться уравновешивающую |
Тело будет вращаться |
Тело будет перемещаться равно-ускоренно |
|
|
8 |
2 |
Как определить равнодействующую двух сил, направленных под углом к друг другу? |
1.2 |
Изображается диагональю параллелограмма, построенного на этих силах |
Нужно построить силовой треугольник из этих сил |
Нужно построить прямоугольник из этих сил |
Силовой треугольник должен быть замкнут |
Параллелограмм разомкнут |
|
|
9 |
2 |
В чем сущность принципа отвердения? |
1.2 |
Равновесие сохраняется и после того как система отвердеет или станет абсолютно твёрдой |
Равновесие нарушается если система отвердеет |
Равновесие на нарушается если тело остановится |
Равновесие нарушается если только остановиться |
Вращение тела прекратиться |
|
|
10 |
2 |
Как определить графически равнодействующую пучка сил на плоскости? |
1.3 |
Нужно построить силовой ногоугольник из этих сил |
Построить параллелограмм |
Построить силовой треугольник |
Построить силовой четырёх угольник |
Построить ромб |
|
|
11 |
2 |
В чём заключается графическое условие равновесия пучка сил на плоскости? |
1.3 |
Силовой многоугольник построенный из этих сил -замкнут |
Силовой треугольник не замкнут |
Равнодействующая равна нулю |
Силовой многоугольник разомкнут |
1.∑xi = 0 2.∑yi = 0 |
|
|
12 |
2 |
В чём заключается аналитические условия равновесия пучка сил на плоскости? |
1.3 |
1.∑xi = 0 2. ∑yi = 0 |
R = 0 |
1. ∑Mx = 0 |
1.∑MA = 0 2.∑MB = 0 |
1.∑MA = 0 2.∑Mi = 0 |
|
|
13 |
2 |
Чему равна проекция равнодействующей силы пучка сил на оси координат? |
1.3 |
Rx = ∑xi Ry = ∑yi |
Rx = Ry = ∑xi |
Rx = Ry = ∑yi |
Rx = Rcos α |
Ry = Rsin α |
|
|
14 |
2 |
Чему равна равнодействующая сила R пучка сил, находящегося в равновесии? |
1.3
|
R = 0 |
R = √Rx2 + Ry2 |
R = √(∑xi)2 + (∑yi)2
|
R = Rα + Ry |
R = Rysinα |
|
|
15 |
2 |
На каком из рисунков правильно построен силовой четырёхугольник трёх сил?
|
1.4 |
b F3 F1 R d a
|
b F d
|
c R d F1 a |
F1
R F2 d |
a F2 b
c |
|
|
16 |
2 |
Какие силы параллельны? |
1.4 |
Направленные в одну сторону, линии действия которых параллельны между собой |
Равные по модулю |
Противоположные по направлению |
Которые на пересекаются |
Которые лежат в одной плоскости |
|
|
17 |
2 |
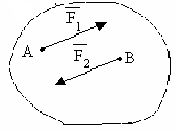
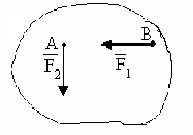
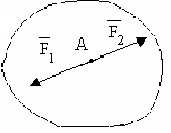
Какие силы антипараллельные? |
1.4 |
Направленые в противоположные стороны, линии действия которых параллельны |
Равные по модулю |
Противоположные по направлению |
Которые лежат в одной плоскости |
Которые не пересекаются |
|
|
18 |
2 |
Что такое пара сил? |
1.4 |
Две равные по модулю антипараллельные силы, приложенные к твёрдому телу |
Две равные по модулю параллельные силы |
Две антипараллельные силы |
Которые не имеют равнодействующей |
Которые не равны по модулю |
|
|
19 |
2 |
Какие две пары будут статистически эквивалентные. |
1.4 |
У которых моменты равные |
У которых моменты разные |
Момент одной пары в два ра-за больше момента второй пары |
У которых плечи равные |
У которых силы равные по модулю
|
|
|
20 |
3 |
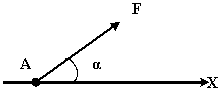
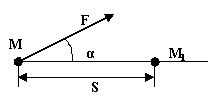
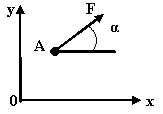
Определить проекции силы на оси х и у
|
1.4 |
X = Fcosα Y = Fsinα |
X = Y= sinα |
Y = tgα |
X = ctgα |
X + Y = F |
|
|
21 |
3 |
В каком случае пары сил находятся в равновесии? |
1.4 |
Если алгебраическая сумма моментов равна нулю |
Если 1.∑xi = 0 2. ∑yi = 0 |
Если МА = 0 |
Если M = Fh |
Если сила параллельна оси |
|
|
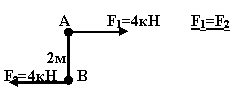
22 |
3 |
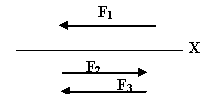
Чему равен момент равнодейс-твующей паре? М1=40кН М2=20кН М3=20кН
|
1.4 |
MR = M1 – M2 – M3 = 40 – 20 – 20 = 0 Пары сил находятся в равновесии
|
MR = M1 = 40 кН |
MR = M1 – M2 = 40 – 20 = 20 кН |
MR = M1 - M3 = 40 – 20 = 20 кН
|
MR = 2M1 = 2 *40 = 80кН |
|
|
23 |
3 |
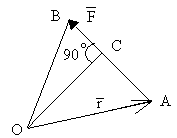
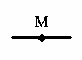
Чему равен момент силы, относительно точки, показанной на рисунке
|
1.4 |
Нулю, так как плечо силы равно нулю |
2F |
F |
3F |
M0 = 2Fl |
|
|
24 |
3 |
Можно ли силу перенести параллельно самой себе в любую точку твёрдого тела? |
1.4 |
Можно, но при этом добавится пара сил |
Нельзя, нарушится равновесие |
Можно, не нарушая равновесия |
Нельзя, при этом тело начнёт пере-мещаться |
Можно, но при этом добавиться две пары сил |
|
|
25 |
3 |
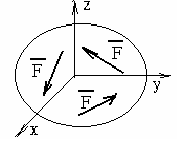
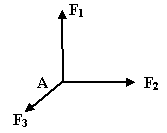
Что необходимо для того чтобы пространственная система сходящихся сил находилась в равновесии? |
1.4 |
Чтобы
|
Чтобы
|
Чтобы
|
Чтобы
|
Чтобы
2. ∑yi = 0
|
|
|
26 |
3 |
Укажите какой вид имеет 1ая форма аналитических условий равновесия плоской системы произвольно расположенных сил? |
1.4 |
|
1. ∑xi = 0 2. ∑МА = 0
|
|
1. ∑МА = 0 2.∑МВ=0
|
|
|
|
27 |
3 |
Укажите какой вид имеет 2ая форма аналитических условий равновесия плоской системы произвольно расположенных сил? |
1.4 |
1. ∑МА = 0 2.∑МВ=0 3. ∑xi = 0
|
1. ∑МА = 0 2. ∑xi = 0
|
1. ∑МА = 0 2.∑МВ=0 3.∑МС=0
|
1.∑МВ=0 2.∑xi = 0 3.∑yi = 0
|
1.∑МА = 0 2.∑yi = 0 3.∑МВ=0
|
|
|
28 |
3 |
Укажите какой вид имеет 3 форма аналитических условий равновесия плоской системы произвольно расположенных сил? |
1.4 |
1. ∑МА = 0 2.∑МВ=0 3.∑МС=0
|
1.∑МА=0 2.∑xi = 0 3.∑yi = 0
|
1. ∑МА = 0 2.∑МВ=0 3. ∑xi = 0
|
1.∑МВ=0 2.∑МС=0 3.∑yi = 0
|
1. ∑МА = 0 2. ∑xi = 0 3.∑МС=0
|
|
|
29 |
3 |
Что необходимо чтобы пучок сил находился в равновесии? |
1.4 |
Силовой многоуголь-ник построенный из этих сил должен быть замкнут |
Необходимо чтобы R = 10F |
Необходимо чтобы R = 2F |
Необходимо чтобы R = 4F |
Необходимо чтобы R = -2F |
|
|
30 |
4 |
Сколько аналитических условий равновесия имеет пространственная система произвольно расположенных сил? |
1.5 |
1. ∑xi = 0 2.∑yi = 0 3.∑zi = 0 4. ∑МX = 0 5. ∑МY=0 6.∑МZ=0 |
1. ∑xi = 0 2.∑МZ=0 3. ∑МY=0
|
1.∑yi = 0 2.∑МZ=0 3. ∑МX = 0
|
1.∑МZ=0 2. ∑МX = 0 3. ∑МY=0
|
1. ∑МX = 0 2. ∑МY=0 3.∑МZ=0
|
|
|
31 |
4 |
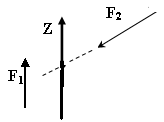
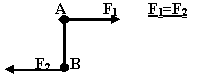
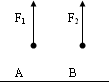
Чему равны моменты изображённых на рисунке сил, относительно оси Z?
|
1.5 |
Нулю, т.к. одна из сил F1, параллельна оси, а вторая F2 её пере-секает в пространстве |
МZ=2F1 |
МZ=2F2 |
МZ=F1 + F2 |
MZ = -(F1/F2) |
|
|
32 |
4 |
Какие аналитические условия равновесия пространственой системы параллельных оси Z сил применимы при решении задач?
|
1.5 |
1.∑Zi=0 2. ∑МX = 0 3. ∑МY=0
|
1. ∑xi = 0 2.∑yi = 0 3.∑МX = 0
|
1. ∑xi = 0 2. ∑МX = 0 3. ∑МY=0
|
1. ∑МX = 0 2. ∑МY=0 3.∑МZ=0
|
1. ∑МX = 0 2.∑МZ=0 3. ∑xi = 0
|
|
|
33 |
4 |
Если силы параллельны оси X в пространстве, то какие условия равновесия применимы?
|
1.5 |
1. ∑XI = 0 2. ∑МY=0 3.∑МZ=0
|
1. ∑xi = 0 2.∑yi = 0 3.∑МX = 0
|
1. ∑xi = 0 2.∑zi = 0 3.∑МY = 0
|
1. ∑xi = 0 2. ∑МX = 0 3.∑МZ=0
|
1. ∑xi = 0 2. ∑МX = 0 3. ∑МZ=0
|
|
|
34 |
4 |
Если силы параллельны оси Y в пространстве, то какие условия равновесия применимы? |
1.5 |
1. ∑yi = 0 2. ∑МX = 0 3.∑МZ=0
|
1. ∑xi = 0 2.∑zi = 0 3.∑yi = 0
|
1. ∑yi = 0 2. ∑МY = 0 3.∑МZ=0
|
1. ∑МX = 0 2.∑МZ=0 3. ∑МY=0
|
1.∑МY = 0 2. ∑xi = 0 3. ∑yi = 0
|
|
|
35 |
4 |
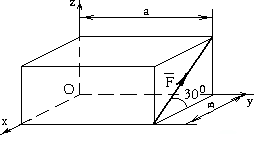
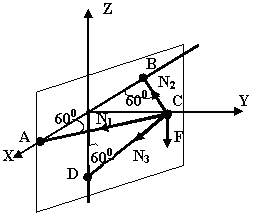
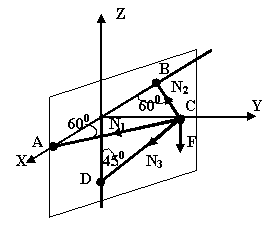
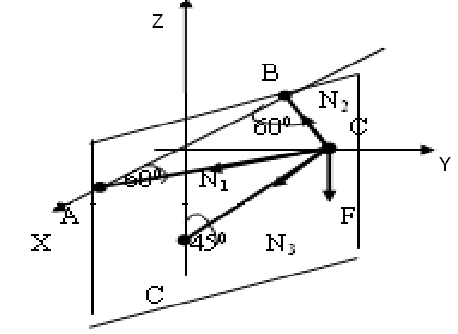
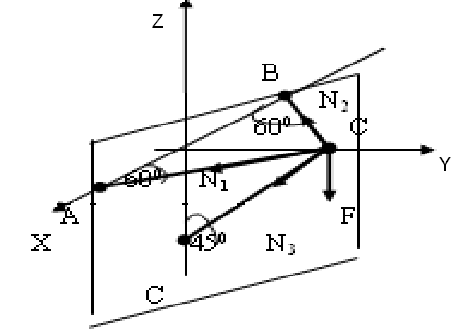
Составить уравнение проекций заданных сил на ось Z
|
1.6 |
∑Zi =0 -F-N3cos450=0 |
∑Zi =0 -F-N3sin650=0 |
∑Zi =0 -2N1-N3cos450=0 |
∑Zi =0 N1-N2- N3=0 |
∑Zi =0 F-N3- N2=0 |
|
|
36 |
3 |
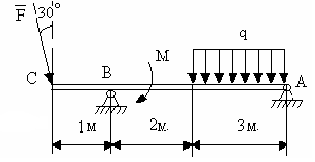
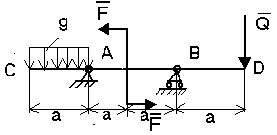
Составить уравнение моментов относительно точки с левой части рамы
|
1.3 |
∑МСЛЕВ= - HA*6 + υA*2 – F*3 – g*2*1=0 |
МС=υA*2
|
МС=υA*2
|
МС=g*2*1+HA*3
|
МС=–F*3 + HA*6
|
|
|
37 |
3 |
Определить уравнение проекций заданных сил на ось Y
|
1.3 |
∑Yi=-N3sin450-N1sin600-N2sin600 |
∑Yi=0 |
∑Yi=-F |
∑Yi= -2N2sin600 |
∑Yi=-2F-N3 |
|
|
38 |
3 |
Определить
уравнение проекций заданных сил на
ось X
|
1.3 |
∑Хi= N1cos600- N2cos600
|
∑Хi=0
|
∑Хi=-F |
∑Хi=-N3cos600-2F |
∑ХC= -2N2cos600-N3 |
|
|
39 |
3 |
Определить
проекции заданных сил на ось Z |
1.3 |
∑ZI=-F-N3*cos450 |
∑ZI=0 |
∑ZI=-2F |
∑ZI= -N3*cos600
|
∑ZI=-F-2N3 |
|
|
40 |
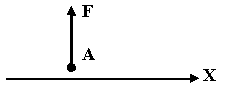
2 |
Что такое центр параллельных сил?
|
1.3 |
Точка через которую проходит линия действия равнодей-ствующей этой системы |
Центр тяжести |
Центр окружности |
Центр шара |
Центр масс |
|
|
41 |
2 |
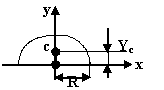
По каким формулам определяется координаты центра параллельных сил на плоскости?
|
1.3 |
|
|
XC=2R YC= 0 |
XC=0.424R YC=0 |
|
|
|
42 |
2 |
Что такое центр тяжести тела? |
1.3 |
Точка, неизменно связанная с телом, через которую проходит линия действия веса тела |
Центр окружности |
Центр шара |
Центр масс |
Центр параллельных сил |
|
|
43 |
2 |
Если сечение имеет две или более осей симметрии, о где находиться её центр тяжести? |
1.4 |
На пересечении этих осей |
В центре |
На расстояние
|
XC=0.424R |
YC=2R/2 |
|
|
44 |
2 |
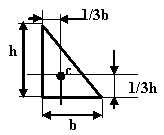
Правильно ли указано на рисунке положение центра тяжести прямоугольного треугольника?
|
1.4 |
Находиться на пересечении двух прямых параллельных катетам, как указанно на рисунке |
Нет |
XC=1/4b YC=1/4h |
XC=0,42h YC=0,2b |
XC=YC=h/2 |
|
|
45 |
3 |
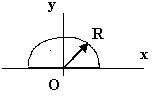
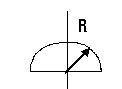
Чему равно расстояние YC у полукруга
|
1.4 |
YC=0,424R |
YC=2R |
YC=D/2 |
YC=R |
YC=R/2 |
|
|
46 |
3 |
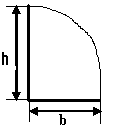
Чему равна площадь параболического треугольника?
|
1.4 |
А=2/3bh
|
А=1/2bh |
А=1/3bh
|
A=bh |
A=2bh |
|
|
47 |
3 |
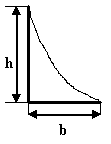
Чему равна площадь параболического треугольника, указанного на рисунке?
|
1.4 |
А=1/3bh
|
А=1/2bh |
А=2/3bh
|
A=bh |
A=2bh |
|
|
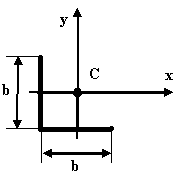
48 |
2 |
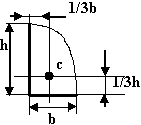
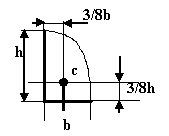
Правильно ли показанно положение центра тяжести фигуры на чертеже?
|
1.4 |
Да XC=3/8b YC=3/8h |
Нет XC=1/2b YC=h |
Нет XC=h/2 YC=b |
Нет XC=h/2 YC=b/2 |
Нет XC=h YC=b |
|
|
49 |
2 |
Как определить площадь полукруга радиуса R? |
1.4 |
А=Пd2/8 |
А=Пd2/4 |
А=Пd2/12 |
А=2Пd2 |
А=4/3ПR2 |
|
|
50 |
2 |
Где находиться центр тяжести у полукруга?
|
1.4 |
На оси симметрии, на расстоянии YC=0,424R от горизонтального диаметра |
YC=2R |
YC=XC=R/2 |
YC=XC=D/2 |
XC=R YC=2R |
|
|
51 |
2 |
Укажите по каким формулам определяются координаты центра тяжести плоской фигуры?
|
1.4 |
|
|
|
|
|
|
|
52 |
3 |
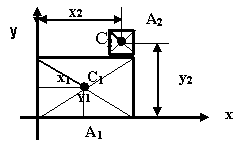
Укажите правильно составленные уравнения для нахождения координат центра тяжести изображённой на чертеже фигуры.
|
1.4 |
|
|
|
|
|
|
|
53 |
3 |
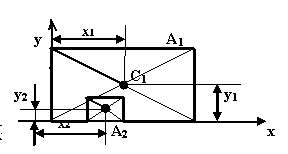
Укажите правильно составленные уравнения координат центра тяжести изображённой на чертеже фигуры
|
1.4 |
|
|
|
|
|
|
|
54 |
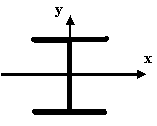
2 |
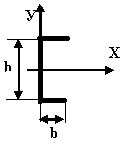
Где находится центр тяжести у двутавра?
|
1.4 |
На пересечении осей симметрии
|
В середине полки |
На вертикальной стенке |
На верхней полке |
На нижней полке |
|
|
55 |
2 |
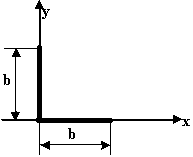
Где находится центр тяжести у равнополочного уголка?
|
1.4 |
На расстояниях ХС=УС от горизонтальной и вертикальной полок |
На расстоянии Z0 от вертикальной полки |
На расстоянии Х0 от стенки |
На оси симметрии |
На бесконечно малом расстоянии от горизонтальной полки |
|
|
56 |
2 |
Где находится центр тяжести у неравнополочного уголка?
|
1.4 |
На расстояниях ХС и УС от вертикальной и горизонтальной полок |
На расстоянии Z0 от вертикальной полки |
На расстояниях Х0=У0 от полок |
На расстоянии ХС=b/2 Y0=b/2 |
На расстоянии ХС=b/2 Y0=b/3 |
|
|
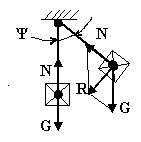
57 |
2 |
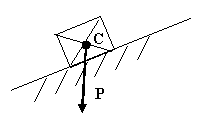
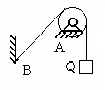
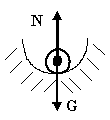
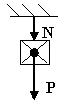
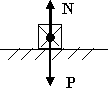
Какое равновесие твёрдого тела имеющего точку подвеса, изображённого на рисунке?
|
1.5 |
Устойчивое, которое восстанавливается после удаления внешних сил силами самой системы
|
Не устойчивое |
Безразличное |
Уравновешенное |
Постоянное |
|
|
58 |
2 |
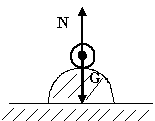
Каким равновесием обозначается тело, изображённое на рисунке?
|
1.5 |
Устойчивым |
Не устойчивым |
Безразличным |
Постоянным |
Уравновешенным |
|
|
59 |
2 |
Каким равновесием обладает тело, изображённое на рисунке
|
1.5 |
Не устойчивым |
Устойчивым |
Постоянным |
Безразличным |
Уравновешенным
|
|
|
60 |
2 |
Каким равновесием обладает тело, изображённое на рисунке
|
1.5 |
Безразличным |
Не устойчивым |
Устойчивым |
Уравновешенным |
Постоянное |
|
|
61 |
3 |
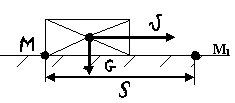
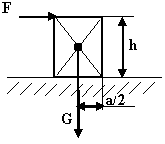
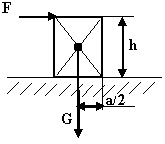
Чему равен опрокидывающий момент?
|
1.5 |
Moн=Fh |
Moн=G(a/2) |
Moн=F(a/2) |
Moн=Gh |
Moн=(F+G)a/2 |
|
|
62 |
3 |
Чему равен удерживающий момент?
|
1.5 |
MY=G(a/2) |
MY=Fh |
MY=Gh |
MY=F(a/2) |
MY=(F+G)a/2 |
|
|
63 |
3 |
Как определяется коэффициент запаса устойчивости? |
1.5 |
KY=MY/Mно |
KY= Mно /MY |
KY= 2Mно |
KY=2MY |
KY=2MY/Mно |
|
|
64 |
2 |
Какие деформации остаточные? |
1.3 |
Которые не исчезают после снятия нагрузки |
Вогнутые |
Выпуклые |
Кручения |
Изгиба |
|
|
65 |
2 |
До каких пор тело будет сохранять состояние покоя? |
1.3 |
Пока другие силы или тела не выведут его из этого состояния |
Постоянно |
Временно |
Пока сохраняется равновесие |
Пока не изменит направление |
|
|
66 |
3 |
Укажите по какой формуле определяется момент силы относительно точки |
1.2 |
MC=±Fh |
MC=F+h |
MC=Fl3 |
MC=2Fb |
MC=F1+F2 |
|
|
67 |
3 |
Что такое центр параллельных сил? |
1.3 |
Точка через которую проходит линия равнодействующей системе параллельных сил |
Точка равновесия тела |
Точка вращения тела |
Точка устойчивости тела |
Точка опрокидывания тела |
|
|
68 |
2 |
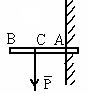
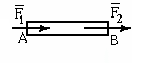
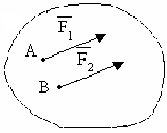
В каком состоянии находяться две равные по модулю силы, изображённые на рисунке?
|
1.2 |
В равновесии |
В движении |
В вращательном движении |
В состоянии несовместимости |
В переносном движении |
|
|
69 |
2 |
Если деформации тела полностью исчезают после снятия нагрузки, то как они называются? |
1.2 |
Упругие |
Остаточные |
Изгиба |
Кручение |
Не восстанавливающиеся. |
|
|
70 |
3 |
Если сила заменяет действие целой системы сил, то как она называется? |
1.2 |
Равнодействующая сила |
Уравновешивающая сила |
Вращательная сила |
Центробежная сила |
Сила инерции |
|
|
71 |
3 |
Связь гибкая нить, может ли реакция связи направлена так, как показанно на рисунке?
|
1.2 |
Нет, реакция может быть направлена только от тела к связи по связи |
Может, если нить отвердеет |
Не, реакция связи должна действовать вне связи |
Силы равны по модулю |
Противоположны по направлению |
|
|
72 |
2 |
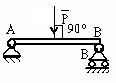
Изменяется ли состояние тела, если силу, показанную на рисунке перенести в точку В?
|
1.2 |
Нет, на основании следствия из 2 и 3 аксиом статики |
Тело начнёт вращаться |
Сила- вектор скользящий |
Сила величина скалярная |
Силу можно заменить системой сил. |
|
|
73 |
3 |
Если сила эквивалентна равнодействующей системе сил, на направление в противоположную сторону по линии действия, то как она называется? |
1.2 |
Уравновешивающей силой |
Противодействующей силой |
Главным вектором |
Главным моментом |
Вектором момента пары сил |
|
|
74 |
2 |
Если линии действия всех сил, действующих на твёрдое тело пересекаются в одной точке, то как называется такая система сил? |
1.2 |
Система сходящихся сил или пучок сил |
Система параллельных сил |
Система произвольно расположенных сил |
Система пространственных сил |
Система сил, лежащих в одной плоскости |
|
|
75 |
3 |
Какая система сил изображаена на рисунке?
|
1.3 |
Пара сил. Две равные по модулю антипараллельные силы |
Две параллельные силы |
Две антипараллельные силы |
Плоская система сил |
Плоская система параллельных сил
|
|
|
76 |
3 |
Как называется тела, препятствующие перемещению абсолютного свободных тел, превращая их в несвободные? |
1.2 |
Называются связями |
Ограничители |
Препятствиями |
Упорами |
Выступами
|
|
|
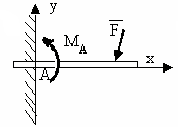
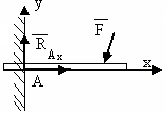
77 |
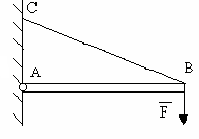
3 |
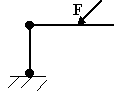
Сколько реакций связей возникает в изображённом виде связи?
|
|
Две, вертикальная υа и горизонтальная На |
Одна, вертикальная υа |
Одна горизонтальная НА |
Одна реактивный момент |
Две, вертикальные υА и реактивный момент МА |
|
|
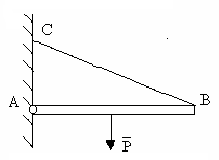
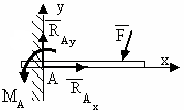
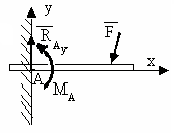
78 |
3 |
Сколько реакций связей возникает в изображённом виде связи?
|
1.2 |
Три – вертикальная υА, горизонтальная НА и реактивный момент в защемлении МА |
Одна – реактивный момент в защемлении МА |
Две – вертикальная υА и горизонтальная НА |
Две, вертикальная υА и реактивный момент в защемлении МА |
Одна вертикальная υА |
|
|
79 |
3 |
Если силовой многоугольник построенный из пучка сил замкнуть то в каком состоянии будет находиться система сил? |
1.2 |
Равнодействующая система сил равна нулю, система сил находиться в равновесии |
Уровновешивающая сила равна нулю |
Равнодействующая сила отрицательна |
Тело движется равномерно |
Тело вращается |
|
|
80 |
2 |
Пары сил, моменты которых равны как называются |
1.3 |
Статический эквивалентны |
Уровновешенные |
Одинаковые |
Вращающие тело по часовой стрелке |
Вращающие тело против часовой стрелки |
|
|
81 |
3 |
Чему равен момент заданной пары сил
|
1.2 |
M=F1*2=4*2 =8кНм |
M=2F1=2*4 =8кН |
M=2F1*2= 2*4*2=16кН |
M=-F2*2=4*2 =8кН |
M=2F2*F1= 2*4*4=32кН2 |
|
|
82 |
4 |
В каком состоянии находиться система пар сил, указанных на рисунке? Чему равен момент равнодействующей паре? М1=20кН М2=20кН М3=40кН
|
1.3 |
В равновесии т.к МR=-М1-М2+М3= -20-20+40=0 |
Вращается по часовой стрелке |
Вращается против часовой стрелки |
Движутся поступательно |
Находится в неопределённом состоянии |
|
|
83 |
2 |
Тела, препятствующие перемещению абсолютно свободных тел, преврая их в несвободные, называются
|
1.2 |
Связями. Горизонтальная опорная поверхность |
Стержнями |
Гибкой нитью |
Шарнирно подвижной опорой |
Жёсткий защемлением |
|
|
84 |
3 |
Сколько реакций возникает в указанном на рисунке виде связи?
|
1.2 |
Одна,перпендикулярна к опорной по-сти и проходящая через центр верхнего, шарнира |
Две –вертикальная и горизонтальная |
Две – вертикальная и реактивным момент |
Две горизонтальная и реактивным момент |
Три вертикальная, горизонтальная и реактивным момент |
|
|
85 |
3 |
Если тело сохраняет за весь период эксплуатации преданную ему форму при изготовлении то оно является? |
1.3 |
Устойчивым |
Безразличным |
Не устойчивым |
Не растягиваться |
Не сжимающиеся
|
|
|
86 |
3 |
Каким являются силы избражённые на рисунке?
|
1.3 |
Параллельными |
Антипараллельными |
Пара сил |
Две силы, направленные в одну сторону |
Направленные по разным линиям действия |
|
|
87 |
3 |
Как определить плечо пары: |
1.2 |
Кратчайшее расстояние между линия -ми действия двух сил |
Сложить силы |
Умножить одну силу на вторую |
Расстояние от начала одной силы до конца второй |
Расстояниек от начала до конца одной силы
|
|
|
88 |
2 |
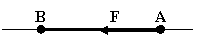
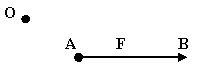
Как определить плечо силы относительно т.о
|
1.2 |
Отпустить перпендикуляр из т.О на линию действия силы F |
Соеденить т А с точкой О |
Соединить т.ОС с точкой В. |
Разделить отрезок АВ на расстояние ОА |
Умножить АВ на расстояние ОА |
|
|
89 |
3 |
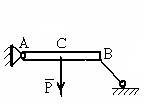
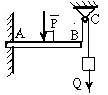
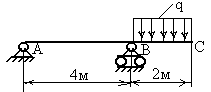
У
|
1.3 |
∑МВ=υА*3+ НА*6-q*6*3-F*1=0 |
∑МВ=υА –F*1-q*6*3=0 |
∑МВ=-υB*6+ НА*6-q*6*3-P*1=0 |
∑МВ=υА*4+ F*3-υA*4=0 |
∑МВ=υА*3+ НА*6-q*6-F*1=0 |
|
|
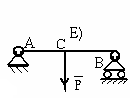
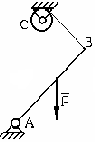
90 |
3 |
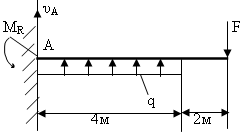
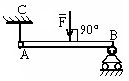
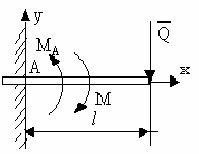
У
|
1.3 |
∑МA=F*6-q*4*2-MR=0 |
∑МA=F*1-q*4*2-MR=0 |
∑МA=F*4-q*4*2+υA-MR=0 |
∑МA=F*5-q*4*3-MR=0 |
∑МA=F*4+υA*5-q*4*2-MR=0 |
|
|
91 |
2 |
Центр тяжести - сила или точка? |
1.4 |
Точка, через которую проходит сила тяжести при любом положении тела в пространстве |
Сила тяжести |
Точка, находящаяся вне тела |
Скорее всего сила, чем точка |
Скорее всего точка, чем сила |
|
|
92
|
2 |
Если сила пересекает ось в пространстве, то чему будет равен момент силы относительно этой оси? |
1.4 |
Нулю, т.к. плечо h равно нулю |
Равен произведению силы на плечо |
Момент будет отрицательным |
Момент будет положительным |
Момент будет нейтральным |
|
|
93 |
2 |
Если сила параллельна оси в пространстве, то чему будет равен момент этой силы относительно оси? |
1.4 |
Равен нулю, т.к. проекция силы на плоскость перпендикулярна оси равна нулю |
Равен произведению силы на плечо |
Момент будет отрицательным |
Момент будет положительным |
Момент будет нейтральным |
|
|
94 |
2 |
Если сила перпендикулярна к оси в пространстве, но не пересекает её, как определить момент силы относительно этой оси? |
1.4 |
Нужно умножить силу на её расстояние от оси |
Нужно удвоить силу |
Нужно умножить силу на ее длину |
Момент равен нулю |
Момент положительный |
|
|
95 |
2 |
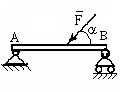
Чему равна проекция силы F на ось Х-?
|
1.4 |
Равны нулю |
Равна самой силе |
Равна удвоенной силе |
X=Fcos900 |
X=Fsin900 |
|
|
96 |
2 |
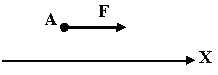
Чему равна проекция силы F на ось Х-?
|
1.4 |
Проекция равна самой силе X=F |
X=0 |
X=F*cos00 |
X=F*sin00 |
X=2F |
|
|
97 |
2 |
Чему
равна проекция силы F
на ось Х
|
1.4 |
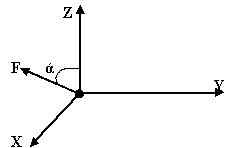
F=cosά |
F=sinά |
X=0 |
X=2F |
X=Ftgά |
|
|
98 |
2 |
Чему равна
проекция силы F
на ось Х-?
|
1.4 |
Х=Fcosά |
Х=Fsinά |
Х=-Fcosά |
Х=Ftgsά |
Х=Fctgsά |
|
|
99 |
2 |
Если заданы 3 параллельные силы на плоскости и известны координаты их точек приложения в выбранной системе координат, то как определить координаты центра параллельных сил? |
1.4 |
|
|
|
XC=0 |
|
|
|
100 |
3 |
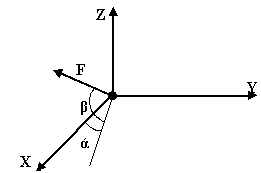
Спроецировать силу на ось Х и У
|
1.3 |
FX=Fcosβ*cosά FY=Fcosβ*sinά |
FY=FX=Fcosβ |
FY=FX=Fsinά |
FX=Fsinά FY=Fcosβ
|
FY=Fsinά FX=Fcosβ
|
|
|
101 |
3 |
Спроецировать силу, лещащую в плоскости ZOY на ось Х
|
1.3 |
FX=0 |
FX=Fcosά |
FX=Fsinά |
FX=2F |
FX=Ftgά |
|
|
102 |
3 |
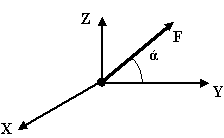
Спроецировать силу, лещащую в плоскости XOY на ось Z
|
1.3 |
FZ=0 |
FZ=Fsinά
|
FZ=Fcosά
|
FZ=Ftgά
|
FZ=Fctgά
|
|
|
103 |
3 |
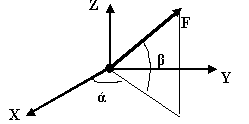
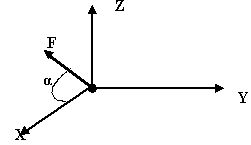
Определить проекции заданной силы на оси Х,Y,Z
|
1.3 |
FX=Fcosβ*cosά FY=Fcosβ*sinά FZ=Fsinβ |
FX=F*cosά FY=F*sinά FZ=Fsinβ |
FX=F*sinά FY=F*cosά FZ=Fcosβ |
FX=Fcosβ FY=Fcosβ FZ=Fsinβ
|
FX=F*cosά FY=F*sinά FZ=Fcosβ |
|
|
104 |
3 |
Спроецировать силу? Лежащую в плоскости XOZ на оси У
|
1.3 |
FY=0 |
FY=Fcosα |
FY=Fsinα |
FY=Ftgα |
FY=Fctgα |
|
|
105 |
3 |
Сила параллельна оси Z в пространстве, определить её проекции на оси X,Y,Z
|
1.3 |
FZ=F FX=0 FY=0 |
FZ=0 FX=F FY=0 |
FZ=0 FX=0 FY=F |
FZ=F FX= -F FY=0 |
FZ=0 FX=0 FY=0 |
|
|
106 |
2 |
Правильно ли показанно положение центра тяжести фигуры на чертеже?
|
1.4 |
Нет, эти расстояния должны быть равные: XC=3/8b YC=3/8h |
Правильно |
Нет эти расстояния должны быть равны XC=YC=1/4h |
Нет, эти расстояния должны быть равны XC=YC=1/4b |
Нет, эти расстояния должны быть равны XC=3/8h YC=5/8h |
|
|
107 |
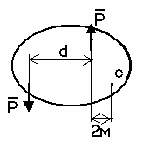
2 |
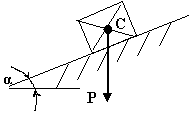
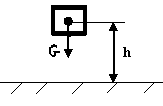
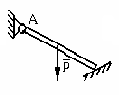
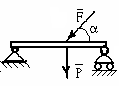
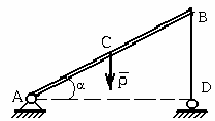
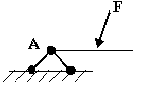
Что произойдёт с телом, находящемся под действием только силы тяжести на наклонной плоскости? Если Р выйдет за пределы площади опоры
|
1.5 |
Тело опрокинется, если линия действия веса тела вышла за пределы площади опоры |
Тело будет двигаться по наклонной плоскости |
Тело будет скользить вверх |
Тело будет сохранять состояние покоя |
Ни чего не произойдёт |
|
|
108 |
3 |
До каких пор тело, находящееся под действием только силы тяжести на наклонной плоскости не опрокинется?
|
1.5 |
До тех пор пока линия действия веса тела не выйдет за пределы площади опоры |
Всегда |
Пока угол наклона плоскости горизонтали будет острым |
Пока угол наклона плоскости будет не более 800 |
Пока угол наклона плоскости будет менее 900 |
|
|
109 |
3 |
С точки зрения устойчивости тела, какое движение транспортных средств предпочтительнее вдоль или поперёк склона |
1.5 |
Поперёк склона, т.к. меньшая вероятность опрокидывания |
Только вдоль склона |
Безразлично |
Только поперёк склона |
Под углом 450 к горизонтали |
|
|
110 |
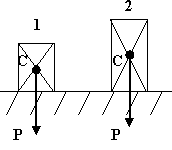
3 |
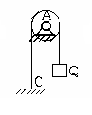
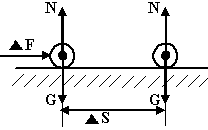
Какое из двух тел будет более устойчивым и почему?
|
1.5 |
Первое, т.к. его центр тяжести находиться ближе к плоскости опоры |
Второе, т.к. его центр тяжести находиться дальше к плоскости опоры |
Первое, т.к. оно меньше по размерам |
Второе, т.к. оно больше но размерам |
Тела обладают одинаковым устойчивостью |
|
|
111 |
3 |
Возможна ли вероятность опрокидывания сооружения телебашня «Останкино» если нет» то почему? |
1.5 |
Нет, т.к. его центр тяжести находиться в пределах плоскости опоры |
Возможна вероятность опрокидывания, т.к. его высота в пределах 350 метров |
Возможна, так как его центр тяжести находится на значительном расстоянии от плоскости опоры
|
Нет, т.к. оно очень малого веса |
Нет, т.к. оно надёжно прикреплено к земле |
|
|
112 |
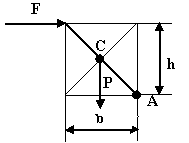
3 |
Определите удерживающий и опрокидывающий моменты тела
|
1.5 |
MY=P*(b/2) Mопр=Fh |
MY=P*b Mопр=Fh |
MY=P*2b Mопр=F(h/2) |
MY=P*b Mопр=Fb |
MY=Mопр=F*P*(b/2)
|
|
|
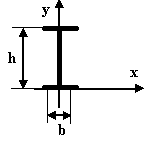
113 |
3 |
Определите координаты центра тяжести изображённого двутавра
|
1.4 |
XC=0 YC=h/2 |
XC=b/2 YC=h/2 |
XC=h/2 YC=b/2 |
XC=YC=h/2 |
XC=YC=b2 |
|
|
114 |
3 |
Как определить центр тяжести полукруга?
|
1.4 |
YC=0,424R |
XC=R/2 YC=2R |
XC=YC=2R |
XC=0,424R YC=0 |
XC=0 YC=0
|
|
|
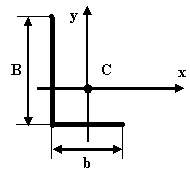
115 |
3 |
Определите координаты центра тяжести швеллера
|
1.4 |
XC=XCтаб YC=h/2 По номеру профиля |
XC=b/2 YC=h/2 |
XC=YC=2h
|
XC=YC=b/2
|
XC=0 YC=h/2
|
|
|
116 |
2 |
Где находится центр тяжести у равнополочного уголка?
|
1.4 |
XC=YC=XCтаб По номеру профиля по таблице |
XC=b/3 YC=b/3 По номеру профиля по таблице |
XC=YC=b/2 По номеру профиля по таблице
|
XC=YC=b2 |
XC=YC=2/3b |
|
|
117 |
3 |
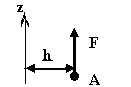
Определить момент силы F относительно оси Z сила параллельна на оси в пространстве
|
1.5 |
MZ=0 т.к проекция силы на плоскость ХОУ равна нулю |
MZ=Fh
|
MZ=2Fh
|
MZ=1/2Fh |
MZ=3Fh
|
|
|
118 |
3 |
Определить момент силы F если сила лежит в плоскости XOZ
|
1.4 |
MZ=0 сила пересекает ось, плечо равно нулю
|
МZ=Fcosα |
MZ=Fsinα |
MZ=Ftgα |
MZ=Fctgα |
|
|
119 |
3 |
Определить момент силы относительно оси Х, если сила лежит в плоскости ХОZ
|
1.4 |
MZ=0 т.к сила пересекает ось, в пространстве |
МZ=Fcosα |
MZ=Fsinα |
MZ=Ftgα |
MZ=Fctgα |
|
|
120 |
2 |
Что такое механическое движение? |
1.5 |
Изменение поло жения тел с течением времени |
Движение молекул |
Движение частей тела |
Броуновское движение |
Тепловое движение |
|
|
121 |
2 |
Если
траектория движения точки выражается
уравнением: то что она собой представляет? |
1.5 |
Эллипс точка движется по Эллипсу |
Окружность |
Точка движется по параболе |
Точка движется по гиперболе |
Точка вращается |
|
|
122 |
3 |
Если траектория движения точки имеет вид: Х2+У2=R2 то что она собою представляет |
1.5 |
Точка движется по окружности |
Эллипс |
Точка движется по параболе |
Точка вращается |
Точка движется по гиперболе |
|
|
123 |
3 |
Если траектория движения точки имеет вид: х2=2у2, то что она собой представляет? |
1.5 |
Гипербола, точка движется по гиперболе |
Эллипс |
Окружность в начале координат |
Парабола |
Кривая линия |
|
|
124 |
2 |
Укажите какие способы задания движения точки существуют |
1.5 |
1.Естественный 2.Координатный 3 векторный |
1.Естественный2.Координатный 3. Полярный |
1.Естественный 2.Координатный
|
1.Под действием силы тяжести 2. Естественный |
1. Свободное падение тела в пространстве 2. Полярный |
|
|
125 |
3 |
Укажите способ задания движения точки: S=3t2+2t |
1.5 |
S=φ(t) – естественный способ |
Координатный способ |
Полярный способ |
Векторный способ |
Свободное падение тела |
|
|
126 |
3 |
Укажите способ задания движения точки: Х=2t y=3t2 z=4t |
1.5 |
Координатный способ задания движения точки |
Естественный способ задания движения точки |
Векторный способ |
Свободное падение тела в пространстве |
Полярный способ движения точка |
|
|
127 |
2 |
Определите способ задания движения точки: r=6t2 |
1.5 |
Векторный способ |
Естественный способ |
Координатный способ |
Полярный способ |
Свободное падение тела |
|
|
128 |
2 |
Что называется скоростью точки? |
1.5 |
Быстрота изменения пути в единицу времени |
Пройденный путь за 2 сек |
Путь, пройденный точкой за 2 час |
Путь от начала отсчёта |
Путь, прой-денный точ-кой за весь промежуток времени |
|
|
129 |
2 |
Как определить скорость при равномерном движении? |
1.5 |
Путь разделить на время υ=S/t |
υ=υ0 |
υX=dx/dt |
υY=dy/dt |
υZ=dz/dt |
|
|
130 |
3 |
Как определить скорость при координатном способе задания движения точки? |
|
υX=dх/dt υY=dy/dt υZ=dz/dt |
υX=υY=dхy/dt |
υZ=υY=dυX/dt |
υX=d2х/dt |
υY=d2y/dt |
|
|
131 |
3 |
Путь пройденый точкой за 1 час равномерного движения S=100м. Опредеилть скорость |
1.5 |
υ=S/t υ=100/1*3600= 0,028м/с |
υ=S/t υ=100/1= 100м/час |
υ=2S=200 м/час
|
υ=S/2=50 м/час
|
υ=2S/1*60= 3,33 м/мин
|
|
|
132 |
3 |
Как определить полную скорость при координатном способе задания движения точки на плоскости? |
1.5 |
υ=√υX2+υY2 υX=dх/dt υY=dy/dt |
υ=υX2+υY2 υX=dх/dt υY=dy/dt |
υ=2υX υX=dх/dt |
υ=υY2 υY=dy/dt
|
υ=υX+υY υX=dх/dt υY=dy/dt |
|
|
133 |
3 |
Движение точки заданного уравнения: S=2t2, определить скорости точки в момент времени t=1c, если S в метрах, t в секундах |
1.5 |
υ=dS/dt =4t υt=1=4*1=4м/c |
υ=dS/dt2 =4м/с2
|
Υ=2*12=2м/с |
Υ=4t2=4*12= 4м/с2 |
Υ=0 |
|
|
134 |
3 |
Движение точки задано уравнением S=4t2+2t. Оопределить скорость точки в момент времени t=2c S(м) |
1.5 |
υ=dS/dt =8t+2 υt=2=8*2+2=18м/с |
υ=dS/dt =St2+2t=36 м/с
|
υ=4*4+4=20 м/с |
υ=12 м/с |
υ=10 м/с |
|
|
135 |
3 |
Определить скорости точки в проекциях на оси координат Х=3t2 Y=4t Z=5t3 |
1.5 |
υX=dx/dt=6t υY=dy/dt=4 м/с υZ=dz/dt=15t2
|
υX=6t2 υY=4t υZ=15t3
|
υX= υY= υZ=15t2 |
υX=υZ=6t+15t2
|
υY=υX= 6t+4t=10t
|
|
|
136 |
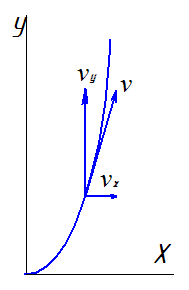
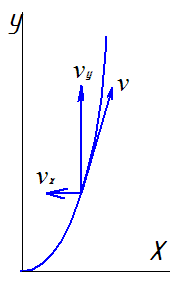
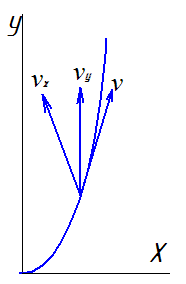
3 |
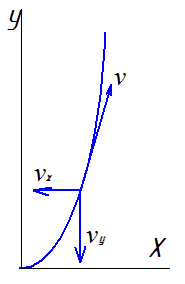
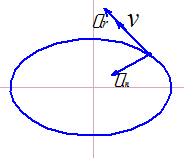
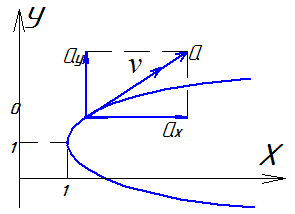
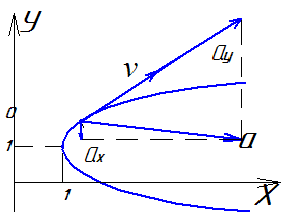
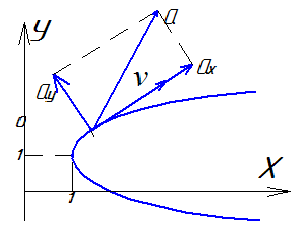
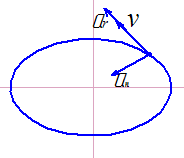
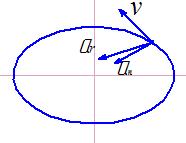
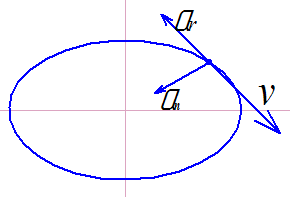
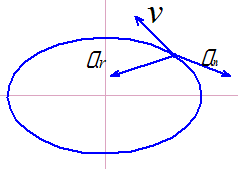
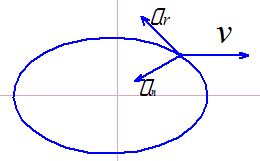
На каком чертеже правильно указано направление полной скорости, если vx=6м/c, vy=8м/с, v=10м/с. |
2 |
|
|
|
|
|
|
|
137 |
3 |
Определить скорость точки при t=2с, если ее движение задано уравнениями x=t3 y=2t3 z=t4 x,y,z
в метрах t
в секундах
|
1.5 |
υX=dx/dt=3t2 υX=12 м/с υY=dy/dt=6t2 υY=24 м/с υZ=dz/dt=4t3 υZ=32 м/с υ= =41.76 м/с |
υX=dx/dt=3t2 υY=dy/dt=6t2 υZ=dz/dt=4t3 υ=√υX2+υY2+υZ2=√3*4+6*4+4*8 =8.26 м/с
|
υX=3t υY=6t υZ=4t υ=υX+υY+υZ= 3t+6t+4t=13t t=2c υ=26 м/с
|
υX=3t υY=6t υZ=4t υ=2υX+υY =13t t=2c υ=24 м/с
|
υX=3t υY=6t υZ=4t υ= υZ+υX= 2t+3t=5t t=2c υ=10 м/с
|
|
|
138 |
2 |
Что называется ускорением? |
1.5 |
Изменение скорости в единицу времени |
Изменение пройденного пути в едини-цу времени |
a=υK-υ0/t |
a=s/υ |
a=2s/t |
|
|
139 |
2 |
Какие виды ускорения точки существует? |
1.5 |
Касательное аτ и нормальное аn |
Угловое ускорение центробежное |
Карилисово ускорение и касательное |
Полное и касательное |
Полное и нормальное |
|
|
140 |
2 |
Как определить касательное ускорение |
1.5 |
aτ=dυ/dt |
aτ=dS/dt |
aτ=υ2/ρ |
aτ=2an |
aτ=d2υ/dt |
|
|
141 |
2 |
Как определить нормальное ускорение? |
1.5 |
aN=υ2/ρ где ρ-радиус кривизны траектории в данной точке |
aN=υ2/2τ |
aN=aτ/2r |
aN=d2S/dt2 |
aN=2ar |
|
|
142 |
2 |
Как определить полное ускорение точки? |
1.5 |
А=√aτ2+an2 |
a=aτ+an |
a=d2S/dt2+υ2/ρ |
a=2an |
A=2aτ |
|
|
143 |
3 |
Точка движется равномерно и прямолинейно. Чему равны касательное и нормальное ускорение? |
1.5 |
аτ=0 аN=0 так как скорость точки не меняется ни по величине, ни по направлению |
aτ= dυ/dt аN=0
|
аτ=0 aτ=υ2/ρ |
аτ=аN=υ2/2τ
|
aτ=d2S/dt2 аN=0
|
|
|
144 |
3 |
Точка движется по прямой, с постоянным ускорением, направленным противоположно скорости. Определите как движется точка |
1.5 |
Равномерно-замедлено (торможение) |
Равномерно |
Равномерно-ускорено |
С переменной скоростью |
С постоянной сколростью |
|
|
145 |
3 |
Какая составляющая ускорения точки характеризует изменение значения скорости? |
1.5 |
Касательное ускорение aτ= dυ/dt
|
Нормальное ускорение аТ=υ2/ρ |
Полное ускорение a=√aτ2+an2 |
Радиальное ускорение |
Центробежное ускорение |
|
|
146 |
3 |
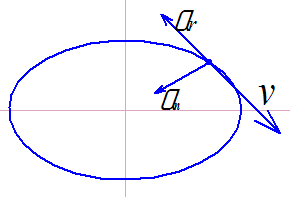
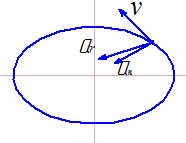
На каком чертеже правильно указаны направление скорости и касательного ускорения, если an=9м/c2, at=-15м/с2, v=19м/с. |
2 |
|
|
|
|
|
|
|
147 |
3 |
Как определить скорость точки при равнопеременном движении? |
1.5 |
υ= υ0+аτt υ0 – начальная скорость точки |
υ=аτt
|
υ=√аNρ где ρ-радиус кривизны траектории |
υ=S/t S- пройденый точкой путь |
υ=S/t
|
|
|
148 |
3 |
Как определить путь при равноускоренном движении точки? |
1.5 |
S=υ0t+aτt2/2 υ 0 -начальная скорость |
S=aτt2/2 υ0≠0 |
S=aN2t/2
|
S=υt |
S=υ0+aNt2/2
|
|
|
149 |
3 |
Ускорение движения поезда аτ= - 0,16 м/с2 Определить время, за которое скорость поезда уменьшиться с 50 до 25 км/ч |
1.5 |
υ= υ0-аτt t=υ0-υ/аτ=(50-25)*103/0.16*3600=42c |
υ= υ0+аτt t= - υ0-υ/аτ=50-25/0.16=15c |
υ= υ0 υ=25км/ч |
υ0-υ/2=t 50+25/2=37.5c |
t=υ0-υ/1ч=50-25/3600=0,06ч |
|
|
150 |
2 |
Какая составляющая ускорения характеризует изменение направления скорости? |
1.5 |
aN=υ2/ρ нормальное ускорение
|
Касательное ускорение aτ= dυ/dt |
Полное ускорение a=√aτ2+an2 |
аτ=0 aτ=υ2/ρ |
аN=0 aτ= dυ/dt
|
|
|
151 |
2 |
Какое движение твердого тела называется поступательными? |
1.5 |
При котором всякая прямая, проведенная в этом теле, останется параллельной самой себе |
При котором тело движется поступательно |
При котором тело вращается |
При котором тело движет-ся равно-ускоренно |
При котором тело движется равнозамедленно |
|
|
152 |
2 |
Что называется вращательным движением тела? |
1.5 |
При котором все точки описывают окружности с центрами, лежащими на оси вращения |
При котором все точки, лежащие на оси вращения остаются неподвижными |
При котором тело поворачивается вокруг неподвижной оси |
При которм тело движет-ся поступа-тельно |
При котором тело поворачивается на некоторый угол |
|
|
153 |
2 |
Что такое угловая скорость тела? |
1.5 |
Изменение угла поворота в единицу времени |
Изменение положения точек тела в 1 секунду |
Угол, выраженный в р/с |
Угол, выраженный в градусах |
Угол поворота тела за всё время вращения |
|
|
154 |
2 |
Как определить угловую скорость при равномерном движении? |
1.5 |
ω=φ/t где φ угол поворота тела |
ω=dφ/dt
|
ω=2φ/2t
|
ω=φ - φ0/2
|
ω=2φ0/t
|
|
|
155 |
3 |
Как определить угловую скорость при переменном вращении? |
1.5 |
ω=dφ/dt
|
ω=dφ/dt2
|
ω=φ/2
|
ω=φ/t
|
ω= ω0+ φ/2
|
|
|
156 |
3 |
Что такое угловое ускорение? Как его определить |
1.5 |
Величина, характеризующая быстроту изменения угловой скорости в единицу времени ε = d ω / dt |
Величина увеличивающая угловую скорость ε= dυ/dt |
Постоянная величина численно равная ε = dυ/dt |
Переменная величина, численно равная ε = d2υ/dt2 |
Постоянная величина численно равная ε =φ/t |
|
|
157 |
3 |
Как определить угловую скорость при равноускоренном вращении |
1.5 |
ω= ω0+Еt ω0-начальная угловая скорость |
ω=Еt
|
ω= φ/t +Еt
|
ω= φ/t +Еt2
|
ω= φ/t |
|
|
158 |
3 |
Как определить угол поворота тела при равноускоренном вращении? |
1.5 |
φ= φ0 + ω0 t+Еt2/2 φ0-угол до начала отсчета |
φ=Еt2/2
|
φ=ω0 t
|
φ= φ0 + Еt2/2
|
φ=ω0 t/2
|
|
|
159 |
3 |
Какая существует зависимость между угловой скоростью и числом оборотов вала в мин. ω и n-? |
1.5 |
ω =Пn/30 |
ω =2Пn/30 |
ω =2Пn |
ω =2Пn/120 |
ω =Пn/60 |
|
|
160 |
3 |
Вал из состояния покоя вращается равноускоренно и за 5 секунд поворачивается на φ=25 рад определить угловое ускорение |
1.5 |
φ=Еt2/2 Е=2φ/t2=2*25/25=2рад/с2
|
φ=ω0 t+Еt Е=φ/t=25/5=5рад/с
|
ω=Еt Е=ω/t
|
φ=ω0 t-Еt2/2 Е=2(φ-ω0 t)/t2
|
Е=0
|
|
|
161 |
2 |
Определить угловую скорость вала, который вращается с n=60об/мин |
1.5 |
ω =Пn/30=3,14*60/30=6,28рад/с |
ω =n/2=60/2= 30об/мин |
ω =Пn=188об/мин |
ω =П/n=3,14/60 =0,05рад/с |
ω =2Пn=120Прад |
|
|
162 |
3 |
Как определить линейную или окружную скорость точек тела при вращении? |
1.5 |
υ=ωr где r – расстояние точки от оси вращения |
υ=dS/dt S- пройденный точкой путь |
υ=2ω0 ω0-начальная угловая скорость |
υ=2(φ/t) φ- угол поворота |
υ=ω0t ω0- начальная угловая скорость тела |
|
|
163 |
3 |
Уравнение движения тела задано уравнением φ=3t2+2t φ (рад) t (с) определите угловую скорость при t=2c |
1.5 |
ω=dφ/dt=6t+2 при t=2c ω=14рад/с
|
ω=dφ/dt=6t2+2t ω=28рад/с
|
ω=dφ/dt=6t+2t =16рад/с
|
ω=dφ/dt=6t+2t2 =24рад/с
|
ω=dφ/dt=6+2= 8рад/с |
|
|
164 |
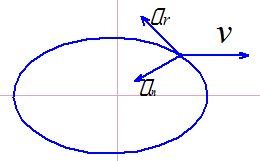
3 |
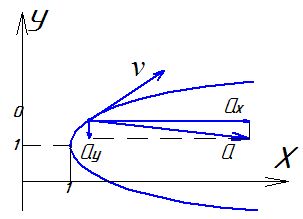
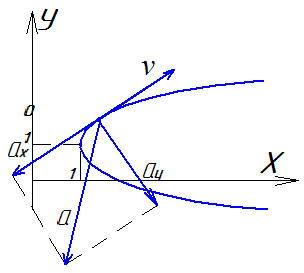
На каком чертеже правильно указаны направление полного ускорения, если aх=8м/c2, aу=-5м/с2, a=9,4м/с2, |
2 |
|
|
|
|
|
|
|
165 |
3 |
Как определить угловое ускорение тела через касательное уравнение? |
1.5 |
Е=dω/dt=d(υR)/ dt=aτR |
Е=aτR
|
Е=aτ /R
|
Е=dω/dt=d2φ/ dt2
|
Е=ω2R
|
|
|
166 |
3 |
Как определить нормальное ускорение через угловую скорость тела? |
1.5 |
an=υ2/R=ω2R2/R=Rω2 |
an=υ2/R |
a=√ a2 - aτ2 |
an=2υ2/R |
an=Еω
|
|
|
167 |
3 |
Если тело вращается равномерно вокруг неподвижной оси, то какая составляющая уравнения равна нулю? |
1.5 |
аτ=0 Е=aτ R=0 аn=ω2R≠0 |
аτ=0 аN=0 Е=aτR=0
|
a=√aτ2+an2=0 |
a=√aτ=0 |
a=аN=υ2/R
|
|
|
168 |
3 |
Твёрдое тело вращается вокруг неподвижной оси с угловой скоростью ω=5рад/с, определить нормальное ускорение точки на расстоянии R=250мм от оси вращения |
1.5 |
аn=ω2R=52*250* 10-3=6,25м/с2 |
an=υ2/R |
аn=ω2R2/R |
an=aτ/2R
|
аn=ωR=5/0.25=20м/с2 |
|
|
169 |
3 |
Тело вращается вокруг неподвижной оси с угловым ускорением Е=20рад/с2 Определить касательное ускорение точки, находящейся на расстоянии R=200мм от оси вращения |
1.5 |
aτ=ЕR=20*200* 10-3=4м/c2
|
aτ=Е/R=20/200* 10-3=1000м/c2
|
aτ=ЕR2=20* 2002=0,8м/c2
|
aτ=0 |
aτ=R/Е=200/20= 10м/c2
|
|
|
170 |
2 |
Что такое мгновенный центр скоростей |
1.5 |
Точка, в которой абсолютная скорость равна нулю |
Точка, в которой угловая скорость равна нулю |
Точка, в которой относительная скорость равна нулю |
Точка, в которой поступательная скорость равна нулю |
Точка, в которой вращательная скорость равна нулю |
|
|
171 |
2 |
Как записывается и читается основной закон динамики? |
1.6 |
F=ma Сила, по величине и направлению равна произведению массы на сообщившее ей ускорение |
F=m/a Равна отношению массы к ускорению
|
F=m/υ2a
|
F=2mυ2 /a
|
F=m1 υ12 /2- m2 υ22 /2
|
|
|
172 |
2 |
Как определить массу тела? |
1.6 |
m=G/g g – ускорение свободного падения |
m=F/a F-действующая сила |
m=2gh h-высота подъёма тела |
m=G/2 G-вес тела |
m=9.81G |
|
|
173 |
2 |
Как читается принцип независимости действия сил? |
1.6 |
Ускорение, полученное точкой от действия системы сил равно геометрической сумме ускорений от действия каждой силы в отдельности |
ma=F1+F2...=∑Fi |
a=F/m |
a=2F/m |
a=3F/m |
|
|
174 |
3 |
Определить действующую на тело силу массой 10кг получившего ускорение а=10м/с2 |
1.6 |
F=ma=10*10= 100Н
|
F=m/a=10/10=1Н
|
F=a/m=10/10=1Н
|
F=ma2=10*100= 1000Н
|
F=m2a=100*10= 1000Н
|
|
|
175 |
3 |
Определить ускорение, полученное телом весом 100Н если приложенная сила равна 100Н |
1.6 |
a=F/m m=G/g a=Fg/G=100*10/ 100=10м/с2
|
a=G/g=100/10 =10м/с2
|
a=F/G=100/ 100=1м/с2 |
a=G/F=100/100 =1м/с2
|
a=GF=100*100 =10000м/с2
|
|
|
176 |
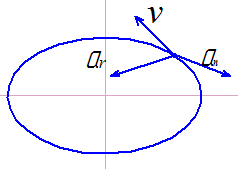
3 |
На каком чертеже правильно указаны направление скорости и касательного ускорения, если an=12м/c2, at=17м/с2, v=23м/с. |
2 |
|
|
|
|
|
|
|
177 |
3 |
Две материальные точки движутся по прямой с постоянными скоростями 10 и 100 м/с. Можно ли утверждать, что к этим точкам приложены эквивалентные системы сил? |
1.6 |
Можно т.к. точки движутся с постоян-ными скоростями по прямым линиям, следовательно под действием уравно-вешенных систем сил (эквивалентна нулю) |
Нельзя, т.к. точки движутся с разными скоростями |
Можно, т.к. ускорения у точек равны нулю |
Можно, т.к. υ 1/ υ2=100/10 =10 |
Нельзя, т.к. υ 1/ υ2=10/100 ≠1 |
|
|
178 |
3 |
К двум материальным точкам массой 5 и 15 кг приложены одинаковые силы сравните численные значения ускорении этих точек. |
1.6 |
Ускорение точки массой 5кг в 3 раза больше ускорения точки массой 15 кг
|
Ускорения одинаковы |
Ускорение точки масс-сой в 5 кг в 3 раза мень-ше ускоре-ния точки в 15 кг |
Ускорения равны нулю |
Ускорения равны произведению масс |
|
|
179 |
2 |
Что такое сила инерции? |
1.6 |
Сила равная произведению массы на ускорение, направленная в сторону, противоположную ускорению |
Сила, равна произведению массы на ускорение |
Сила, равная произведению массы на квадрат скорости |
Сила, равная произведению массы на скорость в третей степени |
Fин=mω2R |
|
|
180 |
2 |
Какие силы инерции существует? |
1.6 |
Касательная и нормальная (центробежная) сила инерции |
Полная и нормальная сила инерции |
Касательная и полная сила инерции |
Вращательная сила инерции |
Поступательная сила инерции |
|
|
181 |
2 |
Как определить касательную силу инерции? |
1.6 |
Fинτ=maτ Fинτ=m(dυ/dt) |
Fинτ=man Fинτ=m(υ2/ρ)
|
Fинτ=mar2
|
Fинτ=man2
|
Fинτ=man ar
|
|
|
182 |
2 |
Как определить нормальную силу инерции? |
1.6 |
Fинn=man Fинn=m(υ2/ρ) |
Fинn=mar Fинn=m(dυ/dt) |
Fинn=man2
|
Fинn=mar2
|
Fинn=man ar
|
|
|
183 |
2 |
В чем заключается принцип Даламбера (метод кинетостатики) |
1.6 |
Если к действующим на тело силам приложить силы инерции, то тело будет находиться в равновесии
|
Задачи динамики можно решать с помощью уравнений равновесия статики |
Fинn=man Fинτ=mar |
F=ma G=mg
|
m=G/g a= F /m
|
|
|
184 |
3 |
Точка массой 500кг движется равномерно по криволинейной траектории со скорости 20м/с радиус кривизны траектории в т.М. равен 100м. Определить центробежную силу инерции |
1.6 |
Fинn=man Fинn=m(υ2/ρ)=500*202/100=2000Н=2кН
|
Fинn=mυ/ρ=500*20/100=100Н |
Fинn=mυ=500*20=1000Н= 1кН |
Fинn=mρ=500* 100=5000= 50кН
|
Fинn=mυρ=50* 100*20=1000кН=1МН
|
|
|
185 |
3 |
Почему рекомендуется снижать скорость автомобиля при проезде по крутым поворотам догори? |
1.6 |
Сила инерции, которая может вызвать опрокидывание автомобиля, прямо пропорциональна квадрату скорости |
т.к. может произойти столкновение с другим транспортным средством |
Из-за плохого обзора может быть авария |
Интенсивный износ автомобильной резины при большой скорости |
Занос при мокром дорожном полотне |
|
|
186 |
3 |
Почему при строительстве автомобильных и железнодорожных дорог строители стремятся построить поворот менее крутым, т.е. с большим радиусом кривизны? |
1.6 |
Так как сила инерции которая может вызвать опрокидывание транспортного средства, обратно пропорциональна радиусу кривизны Fинn=m(υ2/ρ)
|
При малом радиусе кривизны может возникнуть большая аварийность транспортных средств |
Из-за пло-хого обзора при малом радиусе кривизны может быть допущено столкновение |
т.к. при малом радиусе происходит интенсивный износ резины и колёс поезда |
Занос при мокром дорожном полотне |
|
|
187 |
3 |
Укажите куда возможно опрокидывание автомобиля при нарушении правил движения в центр кривизны или наоборот? |
1.6
|
Только в право, в сторону противоположную направлению нормального ускорения |
Возможно влево, возможно в право, зависит от скорости движения |
Только влево |
Опрокидывание не возможно вообще |
Только по направлению скорости υ |
|
|
188 |
3 |
В шахту опускается бадья с ускорением а=4м/с2. Сила тяжести бадьи G=2кН. Определите силу натяжения каната, поддерживающего бадью. |
1.6 |
N=G-FИН FИН=ma=(G/g)a= (2/9.81)*4= 0.815 кН N=2-0.815=1.185кН |
N=ma=(G/g)a= (2/9.81)*4= 0.815 кН
|
N=G=2кН |
N=G-FИН= G+ma=G+(G/g)a=2+0.815=2.815кН
|
N=G-FИН= (G/g)a-G=0,815-2=-1,185кН |
|
|
189 |
2 |
Как
определить работу постоянной силы
показанной на рисунке?
|
1.7 |
W=FScosα |
W=F/Scosα |
W=(F/S)cosα |
W=2FS |
W=Scosα/F |
|
|
190 |
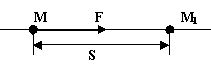
2 |
Чему равна работа на прямолинейном участке, если сила совпадает с направлением движения?
|
1.7 |
W=FS |
W=F/S |
W= S/F |
W=F-S |
W=2FS |
|
|
191 |
2 |
В каких единицах в системе СИ измеряется работа |
1.7 |
Джоуль 1Дж=1нм= 1кгм2/с2 |
Ватт 1Вт |
Ампер 1А |
Килограмм 1кг |
1 ньютон 1Н=0,102кг |
|
|
192 |
2 |
Как определить работу силы тяжести? |
1.7 |
W=GH Произведение силы тяжести на вертикаль-ное перемещение её точки приложения
|
W=mg Произведение массы на ускорение |
W=2GH Удвоенное произведение
|
W=G/H Отношение веса к высоте подъёма |
W=0 |
|
|
193 |
2 |
Укажите, зависит ли работа силы тяжести от траектории подъёма или опускания тела? |
1.7 |
W=GH Не зависит от траектории движения тела
|
W=GH зависит от траектории движения тела
|
W=GH Учитывается только траектория подъёма тела
|
W=GH Учитывается только траек-тория опускания тела
|
W=GH Учитывается вся траектория верх и низ |
|
|
194 |
3 |
Чему равна работа силы тяжести при горизонтальном перемещении тела?
|
1.7 |
Работа силы тяжести равна нулю W=0 |
W=GS |
W=G/S |
W=2G/S |
W=2GS |
|
|
195 |
3 |
Работа постояной силы при прямолинейном перемещении W= - 10Дж. Какой угол составляет направление силы с направлением перемещения? |
1.7 |
Угол тупой, т.к. косинус угла отрицательный W=FScosα |
W=FScosα Угол острый |
W=FScosα Угол прямой |
W=FScosα Угол равен 60 0 |
W=FScosα Угол равен 45 0
|
|
|
196 |
2 |
Что такое мощность? |
1.7 |
P=W/t Работа, совершаемая силой в единицу времени |
P=W2/t
|
P=Wt
|
P=W-t
|
P=W/t2
|
|
|
197 |
2 |
В каких единицах в системе СИ измеряется мощность? |
1.7 |
1Вт=1Дж/с= 1Нм/с 1 ватт |
1кг/с |
1кгм/с |
1ЛС Лошадиная сила |
1кгм/с2 |
|
|
198 |
2 |
Как определяется работа при вращательном движении? |
1.7 |
W=Mφ Произведению вращающего момента на угол поворота |
W=2Mφ
|
W=Mω ω-угловая скорость |
W=M(dφ/dt)
|
W=2M(dφ/dt)
|
|
|
199 |
2 |
Как определить мощность при вращательном движении? |
1.7 |
Р=Mω Произведение вращающего момента на угловую скорость |
Р=M(d2φ/dt2)
|
Р=M2ω Вращающий момент в квадрате на угловую скорость |
Р=Mω2
|
Р=2Mω
|
|
|
200 |
2 |
Как определить кинетическую энергию материальной точки |
1.7 |
T=mυ2/2 |
T=m2υ2/2 |
T=2mυ2 |
T=2m2υ |
T=m2υ/2 |
|
|
201 |
2 |
Как
определить потенциальную энергию
тела?
|
1.7 |
П=Gh h-высота подъёма тела G-сила тяжести |
П=2Gh П-потенциальная энергия G-вес тела |
П=Gh/2 h-высота подъёма тела |
П=Gh2 П-потенциальная энергия
|
П=G2h h-высота подъёма тела G-вес тела |
|
|
202 |
1 |
При каком расположении силы F ее проекция на ось oz равна нулю?
|
С1 |
Сила действует на плоскости Оху |
Сила действует на плоскости Oyz |
Сила действует на плоскости Oxz |
Не совпадает ни с одним из указанных |
Сила параллельна оси Оz |
|
|
203 |
2 |
В каком из приведенных случаев реакция шарнира А направлена вдоль балки АВ? В вариантах A и C весом балки пренебречь. |
С1 |
|
|
|
|
|
|
|
204 |
1 |
В каком из приведенных случаев можно определить линию действия реакции опоры А по теореме о равновесии трех сил?
|
С1 |
|
|
|
|
|
|
|
205 |
1 |
В каком из приведенных случаев реакцию шарнира А нельзя определить по теореме о трех силах?
|
С1 |
|
|
|
|
|
|
|
206 |
1 |
На тело действуют две равные по величине силы F1 и F2. В каком случае тело не будет находиться в равновесии.
|
С1 |
|
|
|
|
Не совпадет ни с одним из указанн |
|
|
207 |
2 |
По какой формуле определяется мо-дуль равнодействующей R двух сил F1 и F2 прило женных к одной точке, если угол между ними < 90° ? |
С1 |
|
|
R =
|
R =
|
R = F1 + F2 ; |
|
|
208 |
1 |
В каком случае на балку АВ действует произвольная плоская система сил? |
С1 |
|
|
|
|
|
|
|
209 |
1 |
Момент силы
|
С2 |
|
|
|
F(в+с) cos |
F(в+с) tg |
|
|
210 |
1 |
В
каком случае момент силы
О найден неверно? |
С2 |
|
|
|
|
Не совпадает ни с одним из указанных |
|
|
211 |
3 |
Вектор момент силы относительно любого центра направлен: |
С2 |
Перпендикулярно к плоскости действия силы и направлен в ту сторону, откуда поворот совершенный силой, виден против хода часовой стрелки |
Вдоль вектора силы |
Перпендикулярно к линии действия силы и лежит в плоскости действия силы |
Перпендикулярно к плоскости действия силы и направлен в ту сторону, откуда поворот совершенный силой, виден в направлении часовой стрелки
|
Не совпадает ни с одним из указанных |
|
|
212 |
2 |
Укажите
в каком из приведенных случаев момент
силы
|
С2 |
|
|
|
|
|
|
|
213 |
3 |
Определить реакцию опоры В,
если интенсивность распределенной
нагрузки q=40
|
С3 |
100H |
. 50H
|
80H |
140H |
120H |
|
|
214 |
2 |
Укажите уравнения равновесия пространственной системы параллельных сил (силы направлены параллельно оси OZ)
|
С3 |
|
|
|
|
|
|
|
215 |
2 |
На каком из рисунков правильно указаны реакции жесткой заделки?
|
С1 |
|
|
|
|
|
|
|
216 |
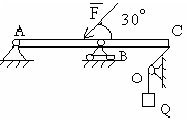
3 |
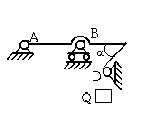
Рычаг весом Р удерживается в равновесии грузом Q. Укажите правильно составлен- ное уравнение равновесия рычага? |
С3 |
|
|
|
|
Не совпадает ни с одной из указанных |
|
|
217 |
1 |
Какая из приведенных систем сил является парой сил? (F1 = F2)
|
С2 |
|
|
|
|
|
|
|
218 |
2 |
Укажите при каких
усло виях
произвольная плоская система сил
находится в равновесии?
|
С3 |
|
|
|
|
Не совпадает ни с одним из указанныx. |
|
|
219 |
2 |
Для однородного бруса АВ веса Р укажите правильно составленное уравнение равновесия вида МА(FK) = 0?
|
С3 |
PAC + RBDAB = 0 |
PAC - RBDAB = 0 |
PAC - RBD · AB cos
|
PAC + RBD · AB sin |
PAC cos
|
|
|
220 |
2 |
В каком случае произвольная плоская система сил приводится к равнодействующей приложенной в центре приведения?
|
С3 |
|
|
|
|
Не совпадает ни с одним из указанных |
|
|
221 |
3 |
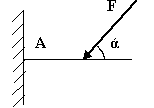
В
каком из приведенных ответов реакция
F = 4кн,
|
С3 |
RA=4.11 kH |
RA=3.51 kH |
RA=2.8 kH |
Не совпадает ни с одним из указанных |
RA=3.31 kH |
|
|
222 |
3 |
К однородной балке, вес которой равен G, длина l, приложены сила Q и пара сил с моментом М. Определить реакции в месте заделки.
|
С3 |
|
|
|
|
Не совпадает ни с одним из указанных |
|
|
223 |
1 |
Чему
равна сумма моментов сил пары
|
С2 |
12Нм |
14Нм |
10Нм |
8Нм |
6Нм |
|
|
224 |
2 |
На двух консольную горизонтальную балку действует пара сил (F, F), на левую консоль равномер но распределенная нагрузка интенсивности g, а в точке D правой консоли вертикально составленная нагрузка Q. Определить правильно составленное уравнение в виде∑Fу=0
|
С3 |
|
RA+RB-ga-Q+FA=0 |
RA+RB+Q-ga=0 |
RA+RB+FA+Q-ga =0 |
-RA-RB –Q-FA+ga =0 |
|
|
225 |
2 |
По
заданным уравнениям движения точки
|
К1 |
|
|
|
|
|
|
|
226 |
2 |
Точка
М движется согласно уравнениям
|
К1 |
|
|
|
|
|
|
|
227
|
2 |
Уравнение движения точки определяются равенствами
Определить закон движения точки по траектории. |
К1 |
|
|
|
|
|
|
|
228 |
1 |
Какое из заданных уравнений соответствует равномерному движению точки? |
К1 |
|
|
|
|
|
|
|
229 |
2 |
Точка движется по указанным траекториям равноускорено? В каком случае полное ускорение точки равно тангенциальному ускорению? |
К1 |
|
|
|
|
|
|
|
230 |
1 |
Точка
движется прямолинейно по закону
|
К1 |
|
|
|
|
|
|
|
231 |
2 |
Точка
движется по окружности согласно
уравнению
|
К1 |
|
|
|
|
|
|
|
232 |
2 |
Определить среднее ускорение точки за промежуток времени между 2-ой и 4-ой секундами, если уравнение ее движения задано в виде: |
К1 |
аср.= 42м/с2 |
аср.= 15м/с2 |
аср=28,5м/с2 |
аср.= 54м/с2 |
аср.= 34м/с2 |
|
|
233 |
2 |
Точка движется по окружности радиуса R= 0,5м согласно уравнению S=0,5t2+2t(м). Определить нормальное ускорение точки в момент времени t= 4с.
|
К1 |
|
|
|
|
|
|
|
234 |
2 |
По какой формуле определять ускорение точки, если ее движение заданно естественным способом? |
К1 |
|
|
|
|
|
|
|
235 |
2 |
Точка движется
по криволинейной траектории. Определить
радиус кривизны траектории точки в
момент времени, когда ее скорость
равна 3м/с, а полное ускорение 6 |
К1 |
|
|
|
|
|
|
|
236 |
1 |
Тело
вращается по закону
|
К3 |
|
|
|
|
|
|
|
237 |
2 |
Твердое
тело вращается равномерно вокруг
своей оси с угловой скоростью
|
К3 |
|
|
|
|
|
|
|
238 |
2 |
Ротор турбины имеет угловую скорость, соответствующую n = 3600 об/мин. Вращаясь равнозамедленно, он уменьшил вдвое угловую скорость за 12 секунд. Сколько оборотов сделал ротор за это время?
|
К3 |
|
|
|
|
|
|
|
239 |
1 |
По какой из формул следует определить окружную скорость точки вращающегося тела? |
К3 |
|
|
|
|
|
|
|
240 |
2 |
Маховик вращается равномерно вокруг своей оси делая 600 об/мин. Какова угловая скорость маховика? |
К3 |
|
|
|
|
|
|
|
241 |
2 |
Точка движется равнопеременно по криволинейной траектории с касательным ускорением a=3 м/с2. Определить нормальное ускорение точки в момент времени когда ее полное ускорение равно а=5 м/с2. |
К1 |
4 м/с2 |
2 м/с2 |
1 м/с2 |
3 м/с2 |
5 м/с2 |
|
|
242 |
2 |
Ротор электродвигателя начав вращаться равноускоренно из состояния покоя, сделал за первые 5с. 100 оборотов. Определить угловое ускорение ротора? |
К3 |
|
|
|
|
|
|
|
243 |
2 |
Нормальное
ускорение точки обода диска вращающегося
вокруг неподвижной оси, равна 6,4 м/с
? Определить угловую скорость
|
К3 |
|
|
|
|
|
|
|
244 |
2 |
Модуль ускорения Кориолиса определяется по формуле: |
К2 |
|
|
|
|
|
|
|
245 |
3 |
Какова физическая сущность ускорения Кориолиса?
|
К2 |
Кориолисово ускорение точки характеризует изме-нение относительной скорости при перено-сном и изменение переносной скорости в относительном движении;
|
Кориолисово ускорение точки характеризует изменение ее переносной скорости при относительном движении; |
Кориолисово ускорение точки харак-теризует изменение ее относи-тельной скорости при переменном движении; |
Кориолисово ускорение точки характеризует изменение величины и направления ее ускорения когда переносное движение поступательное; |
Кориолисово ускорение точки характеризует изменение величины и направления ее скорости когда переносное движение вращательное |
|
|
246 |
2 |
По какой формуле определяется абсолютное ускорение точки при сложном ее движении, если переносное ее движение – поступательное.
|
К2 |
|
|
|
|
|
|
|
247 |
2 |
Какими уравнениями задается плоско-параллельное движение твердого тела.
|
К4 |
|
|
= (t); |
S=S(t);
|
|
|
|
248 |
2 |
В каком случае кориолисово ускорение точки не равно нулю? |
К2 |
|
|
|
|
|
|
|
249 |
2 |
Уравнение вращения
маховика вокруг своей оси
|
К2 |
12сек |
5 сек |
3сек |
9 сек |
15сек |
|
|
250 |
2 |
Движение точки по дуге окружности радиуса R=18м. описывается уравнением S=(3t2 + 2)м Определить полное ускорение точки через t = 2сек. |
К1 |
10м/с |
12м/с |
8м/с |
6м/с |
4м/с |
|
|
251 |
1 |
. Дано нормальное an = 4 м/с2 и касательное ar = 3 м/с2 ускорения точки. Определить полное ускорение точки.
|
К1 |
5м/с2 |
1м/с2 |
7м/с2 |
9м/с2 |
6м/с2 |
|
|
252 |
2 |
Определить нормальное ускорение точки в момент времени когда ускорение точки а = 10 м/с2 , а угол между векторами скорости и ускорения равен 450.
|
К1 |
7,07 м/с2 |
5 м/с2
|
8,66 м/с2 |
6,06 м/с2 |
9,16 м/с2 |
|
|
253 |
2 |
Точка движется по окружности радиус которой r = 50см, со скоростью v = 2t м/с. Определить модуль нормального ускорения в момент времени t = 10сек.
|
К1 |
400 м/с2 |
200 м/с2 |
300 м/с2
|
500 м/с2 |
600 м/с2 |
|
|
254 |
3 |
Естественными уравнениями движения материальной точки |
7 |
|
|
|
|
|
|
|
255 |
1 |
Дифференциальное уравнение свободных колебаний материальной точки |
8 |
|
|
|
|
|
|
|
256 |
1 |
Уравнения гармонических колебаний |
8 |
|
|
|
|
|
|
|
257 |
1 |
Дифференциальное уравнение затухающих колебаний |
8 |
|
|
|
|
|
|
|
258 |
1 |
Формула связи периодов свободных и затухающих колебаний |
8 |
T*= |
|
|
|
|
|
|
259 |
2 |
Формула коэффициента динамичности |
9 |
|
|
|
T*= |
|
|
|
260 |
3 |
Дифференциальные уравнения движения материальной точки по криволинейной поверхности в форме Лагранжа |
9 |
|
|
|
|
|
|
|
261 |
1 |
Уравнение движения материальной точки в форме Л.Эйлера |
10 |
|
|
|
|
T*= |
|
|
262 |
2 |
Уравнение динамики относительного движения материальной точки |
10 |
|
|
|
|
|
|
|
263 |
3 |
Дифференциальное уравнение относительного движения материальной то- чки в координатной форме
|
10 |
|
|
|
|
|
|
|
264 |
1 |
Момент инерции твердого тела относительно плоскости |
11 |
|
|
|
|
|
|
|
265 |
2 |
Момент инерции твердого тела относительно оси |
13 |
|
|
|
|
|
|
|
266 |
3 |
Момент инерции твердого тела относительно центра |
13 |
|
|
|
|
|
|
|
267 |
1 |
Момент инерции твердого тела в общем случае |
13 |
|
|
|
14 |
|
|
|
268 |
1 |
Чему равно количество движения материальной точки. |
14 |
Равно произведению массы материальной точки на ее скорость |
Равно произведению объема мате-риальной точки на ее ускорение |
Равно произведе- нию плотности материальной точки на ее скорость |
Равно произведению массы материальной точки на ее объем |
Равно произведе- нию массы материальной точки на ее плотность |
|
|
269 |
3 |
Дифференциальное уравнение Лагранжа ІІ рода для консервативной системы. |
14 |
|
|
|
|
|
|
|
270 |
1 |
Формула изменения количества движения механической системы равно сумме импульсов внешних сил |
14 |
|
|
|
|
|
|

 F2 с
F2 с





 1
F2 с
1
F2 с R F3
R F3


 F2 F3
F2 F3 b
b
 b
b
 a F3 c
a F3 c

 R F1
R F1

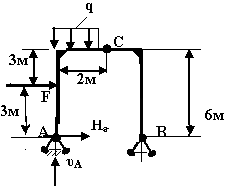
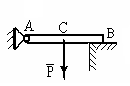
 кажите
где правильно составлено уранение
равновесия:∑MB?
кажите
где правильно составлено уранение
равновесия:∑MB?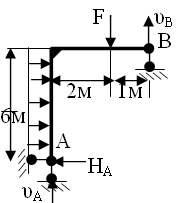


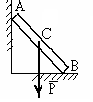
 кажите
где правильно составлено уравнение
равновесия ∑МА?
кажите
где правильно составлено уравнение
равновесия ∑МА?