
Matematika_1_NGD-kaz-1-sem
.doc|
Анықтауышты
есептеңіз
|
-1 |
|
Анықтауышты
есептеңіз
|
1 |
|
Кері
матрицаны
табыңыз
|
|
|
Матрицаның
а12
элементінің
М12
минорын
есептеңіз
|
-30 |
|
Матрицаны
транспонирлеңіз
|
|
|
Егер
А= |
|
|
Егер
А= |
|
|
Егер
А= |
|
|
Теңдеулер
жүйесін
шешіңіз.
|
(3;1;1) |
|
Матрицаның рангысын табыңыз. А= |
2 |
|
|
(5,2) |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
3 |
|
|
13 |
|
|
5 |
|
Х-тің
қандай
мәнінде
|
- |
|
y-тің
қандай
мәнінде
|
-3 |
|
2х+3у-6=0 түзуі Ох осін қандай нүктеде қиып өтеді? |
(3,0) |
|
A(-1,3), B(4,-2) нүктелері арқылы өтетін түзу теңдеуін жазыңыз. |
х+y-2=0 |
|
А(1;3), В(2;4) нүктелері арқылы өтетін түзу теңдеуін жазыңыз. |
х-у+2=0 |
|
А(0;1), В(1;0) нүктелері арқылы өтетін түзу теңдеуін жазыңыз. |
x+у-1=0 |
|
Координаталар басы және А(-1;-8) нүктесі арқылы өтетін түзу теңдеуін жазыңыз. |
у=8х |
|
Координаталар басы және А(2;5) нүктесі арқылы өтетін түзу теңдеуін жазыңыз. |
5x-2y=0 |
|
у= |
2/3 |
|
у= |
3 |
|
М |
7 |
|
А(-3,1),В(7,8) нүктелері арқылы өтетін түзудің бұрыштық коэффициентін табыңыз.. |
|
|
3х+2у-1=0 түзуінің бұрыштық коэффициентін табыңыз. |
к= |
|
Координат остерінен 3 және 5 тең кесінді қиып өтетін түзу теңдеуін жазыңыз. |
|
|
Шеткі нүктелері А(3;2) және В(12;8) нүктелері болатын түзу кесіндісі үш тең бөлікке бөлінген. Бөліну нүктелерінің координаталарын анықтаңыз. |
(6;4), (9;6) |
|
А(-1;5) нүктесінен 4x+3y-5=0 түзуіне дейінгі қашықтықты табыңыз. |
|
|
А(2;3) нүктесінен 3х+4у-3=0 түзуіне дейінгі қашықтықты табыңыз. |
3 |
|
х-2у+3=0 түзуі координат басынан қандай қашықтықта орналасқан. |
|
|
Берілген түзулердің қайсысы у=3х+5 түзуіне параллель а)
у= в)
у= |
в |
|
Параллель түзулерді көрсетіңіз. а) 6х+у-3=0, б) х-6у-3=0, в) 12х+2у+7=0, г) 6х-у+3=0 |
а, в |
|
Перпендикуляр түзулерді көрсетіңіз. а) х+у=0, б) 10х-6у+1=0, в) у+1=0, г) 3х+5у-9=0 |
б, г |
|
2х-7у+14=0 түзу теңдеуін кесінділік теңдеу түріне келтіріңіз. |
|
|
у=-2х, у=3х+5 екі түзу арасындағы бұрышты табыңыз. |
|
|
А(1;-2), |
|
|
М(4;-7) нүктесі арқылы өтетін Оу осіне параллель түзу теңдеуін жазыңыз. |
х-4=0 |
|
4x+3y-5=0 түзуінің нормалаушы көбейткішін табыңыз. |
|
|
Егер
нормальдың
ұзындығы
р=3
тең,
ал
оның
Ох
осінің
оң
бағытымен
жасайтын
|
|
|
а-ның қандай мәнінде (a+3)x+ay+4=0 түзуі абсцисса осіне параллель болады? |
-3 |
|
а-ның қандай мәнінде (a+3)x+ay+4=0 түзуі ордината осіне параллель болады? |
0 |
|
Төбелері А(3;2), В(5;-2), С(1;0) болатын АВС үшбұрышының ВМ медианасының теңдеуін жазыңыз. |
х+у-3=0 |
|
Р(-8;12) нүктесінің А(2;-3) және В(-5;1) нүктелері арқылы өтетін түзуге түсірілген проекциясын табыңыз. |
(-12;5) |
|
А(-4;5) нүктесі диагоналі 7х-у+8=0 түзуінде жататын квадрат төбесі. Осы квадраттың екінші диагоналінің теңдеуін жазыңыз. |
х+7у-31=0 |
|
х+2у-z-2=0 жазықтығының нормаль векторын көрсетіңіз. |
(1,2,-1) |
|
|
x-2y-3z-4=0 |
|
|
-3y+4z+13=0 |
|
2x-y+3z+6=0 жазықтығының Ох осімен қиылысу нүктесін табыңыз. |
(-3;0;0) |
|
x+y+z-6=0, 3x-y+z-4=0, 2x+y-z-1=0 жазықтықтарының қиылысу нүктесін табыңыз. |
(1;2;3) |
|
Параллель жазықтықтарды көрсетіңіз. а) 4x-6y+3z+6=0, б) 2x-3y+z-5=0, в) x+y+z+6=0, г) 8x-12y+6z-1=0. |
а, г |
|
Перпендикуляр жазықтықтарды көрсетіңіз. а) 2x-y+2z+9=0, б) x-3y+z-5=0, в) x+4y+z-7=0, г) 4x-6y+3z+6=0. |
а, в |
|
|
|
|
М(1;-2;4) нүктесі арқылы өтетін Охz жазықтығына параллель жазықтық теңдеуін жазыңыз. |
у+2=0 |
|
x-2y+2z-8=0, x+ -6=0 жазықтықтарының арасындағы бұрышты табыңыз. |
|
|
М1(3;-1;2), М2(4;-1;-1), М3(2;0;2) нүктелері арқылы өтетін жазықтық теңдеуін жазыңыз. |
3х+3у+z-8=0 |
|
А(3;-1;2)
және
В(4;-2;-1)
нүетелері
берілген.
А
нүктесі
арқылы
өтетін
|
x-у-3z+2=0 |
|
(2;3;-4) нүктесінен 2х+6у-3z+16=0 жазықтығына дейінгі қашықтықты тап. |
|
|
М(1;1;1) нүктесінен 3x+4y+7=0 жазықтығына дейінгі қашықтықты табыңыз. |
2,8 |
|
x-y+z-1=0, 2x-2y+2z-5=0 параллель жазықтықтарының ара қашықтықтарын табыңыз. |
|
|
Координат остерінің x+2y+4z-4=0 жазықтығымен қиғандағы кесінділерін тап. |
а=4, в=2, с=1 |
|
2x+3y-8z-24=0 жазықтығының теңдеуі берілген. Жазықтықтың кесіндідегі теңдеуін жаз. |
|
|
2х-2у+z-18=0 жазықтығының нормалаушы көбейткішін табыңыз. |
|
|
3x+2y+6z-4=0 жазықтығының нормальдық теңдеуін жазыңыз. |
|
|
Координаттық жазықтықтардың теңдеулерін жазыңыз. |
х=0, y=0, z=0 |
|
A(-1,2,3), B(2,6,-2) нүктелері арқылы өтетін түзу теңдеуін жазыңыз. |
|
|
Координат бас нүктесі және (-2;5;-3) нүктесі арқылы өтетін түзу теңдеуін жаз. |
|
|
А(1;-2;1), В(3;1;-1) нүктелері арқылы өтетін түзудің канондық теңдеуін жазыңыз. |
|
|
А(1;1;1), В(3;-2;2) нүктелері арқылы өтетін түзудің канондық теңдеуін жазыңыз. |
|
|
|
|
|
|
|
|
М(2;-3;1)
нүктесі
арқылы
өтетін
|
|
|
А(-2,1,-1)
нүктесі
арқылы
өтетін
|
|
|
М(2;-3;-5) нүктесі арқылы өтетін 6x-3y-5z+2=0 жазықтығына перпендикуляр түзу теңдеуін жазыңыз. |
|
|
М(2;-3;1)
нүктесі
арқылы
өтетін
|
|
|
М(1;-1;3) нүктесі арқылы өтетін 3x+2y+4z-7=0 жазықтығына перпендикуляр түзу теңдеуін жазыңыз. |
|
|
М(2;0;3)
нүктесі
арқылы
өтетін
|
3x+6y+2z-12=0 |
|
|
|
|
2x-y+z+3=0 жазықтығының арасындағы бұрышын табыңыз. |
|
|
|
-
|
|
|
(2;-1;0) |
|
|
(4;-5;1) |
|
|
(3;-3;0) |
|
|
|
|
x- |
|
|
|
|
|
|
|
|
Шеңбердің
теңдеуін
құрыңыз,
егер ол координаттар бас нүктесі
арқылы
өтетін
және
оның
центрі
|
|
|
Эллипстің
теңдеуін
құрыңыз,
егер оның
жарты остері
|
|
|
Эллипстің канондық теңдеуін құрыңыз. |
|
|
Шеңбердің канондық теңдеуін табыңыз. |
|
|
Эллипстің
теңдеуін
құрыңыз,
егер оның
жарты остері
|
|
|
Шекті
есептеңіз:
|
-16 |
|
Шекті
есептеңіз:
|
1 |
|
Шекті
есептеңіз:
|
|
|
Шекті
есептеңіз:
|
4/3 |
|
Шекті
есептеңіз:
|
1 |
|
Шекті
есептеңіз:
|
-2/3 |
|
Шекті
есептеңіз:
|
1/3 |
|
Шекті
есептеңіз:
|
2 |
|
Шекті есептеңіз:
|
|
|
Шекті
есептеңіз:
|
4/5 |
|
Шекті
есептеңіз:
|
|
|
Шекті
есептеңіз:
|
-1/2 |
|
Шекті
есептеңіз:
|
0 |
|
Шекті есептеңіз:
|
1 |
|
Шекті
есептеңіз:
|
0 |
|
Шекті
есептеңіз:
|
|
|
Шекті
есептеңіз:
|
|
|
Шекті
есептеңіз:
|
-1/4 |
|
Шекті
есептеңіз:
|
0 |
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
0 |
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны
табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны
табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны табыңыз:
|
|
|
Туындыны
табыңыз
|
|
|
Туындыны табыңыз
|
|
|
Туындыны
табыңыз
|
|
|
|
|
|
Туындыны
табыңыз
|
0 |
|
Туындыны
табыңыз
|
|
|
Туындыны табыңыз
|
|
|
Егер
|
2 |
|
Егер
|
2,5 |
|
Егер
|
|
|
|
|
|
|
0 |
|
|
6 |
|
|
-4 |
|
Табу
керек:
|
1 |
|
Табу
керек:
|
1 |
|
Қандай нүктелерде кубтық параболаның бұрыштық коэффициенті 3-ке тең? |
(1,1) және (-1,-1) |
|
|
|
|
Материалдық
нүктенің
қозғалысының
теңдеуі
берілген:
|
26 |
|
|
-1 |
|
|
|
|
|
|
|
Табу
керек:
|
|
|
|
|
|
|
(- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Иілу нүктесі жоқ |
|
Есептеңіз:
|
-1 |
|
Есептеңіз:
|
|
|
Есептеңіз:
|
-8 |
|
Есептеңіз:
|
2 |
|
Есептеңіз:
|
|
|
-
|
|
|
Берілген
f(x),x |
F(x)-үздіксіз
функция: |
|
|
f(x)
функциясының
барлық
алғашқы
|
|
|
|
|
|
|
|
|
Элементар функцияларда интегралданбайды |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегралды есептеңіз.
|
|
|
Интегралдау
әдісін
көрсет. |
Анықталмаған коэффициенттер әдісі |
|
Анықталмаған интеграл үшін бөлшектеп интегралдау формуласы. |
|
|
Интегралды
есептеңіз
|
|
|
Интегралды
есептеңіз
|
|
|
Интегралды
есептеңіз
|
|
|
Интегралды есептеңіз
|
|
|
Меншіксіз
интегралды есептеңіз
|
|
|
Меншіксіз
интегралды есептеңіз
|
жинақсыз |
|
Интегралды
есептеңіз
|
|
|
Интегралды
есептеңіз
|
жинақсыз |
|
Интегралды
есептеңіз
|
2 |
|
Берілген
алмастыру арқылы
анықталған
интегралды түрлендіріңіз |
|
|
Берілген
алмастыру арқылы
анықталған
интегралды түрлендіріңіз
|
|
|
Берілген
алмастыру арқылы
анықталған
интегралды түрлендіріңіз
|
|
|
Берілген
алмастыру арқылы
анықталған
интегралды түрлендіріңіз
|
|
|
Берілген
алмастыру арқылы
анықталған
интегралды түрлендіріңіз
|
|
|
Қандай алмастыру қолдануға болады
|
|
|
Теңдеуді шешіңіз
|
|
|
Интегралды есептеңіз
|
|
|
Интегралды есептеңіз
|
|
|
Берілген аралықтағы функцияның орта мәнін табыңыз
|
|
|
Келесі сызықтармен шектелген фигураны салыңыз
|
|
|
Келесі сызықтармен шектелген фигураны салыңыз
|
|
|
|
|
|
Полярлық
координаталар жүйесінде
|
шеңбер |
|
Келесі сызықтармен шектелген фигураны салыңыз
|
|
|
|
Сегіз жапрақты раушангүл |
|
Шектері бірдей анықталған интегралдың мәні неге тең? |
0 |
|
|
|
|
|
|
|
|
|
|
Астроидамен
шектелген фигураның
ауданын есептеңіз
|
|
|
|
|
|
Декарттық координат жүйесіндегі доғаның ұзындығының формуласы. |
|
|
Параметрлік теңдеумен берілген доғаның ұзындығы. |
|
|
Поляр координаталарымен берілген доғаның ұзындығы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|



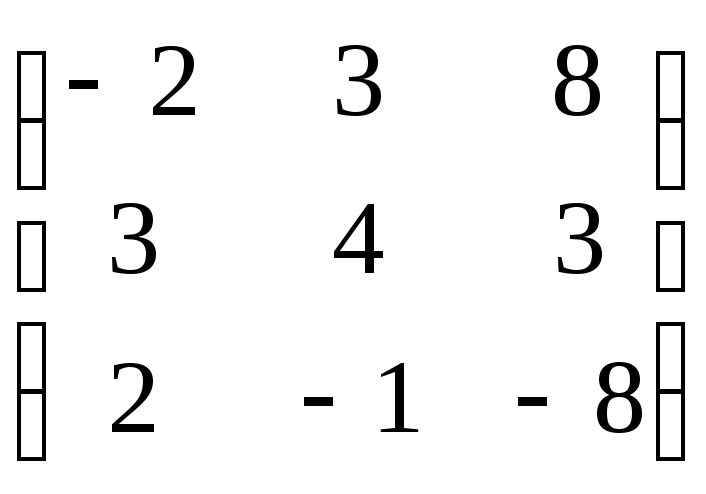


 болса, АВ
көбейтіндісін
табыңыз.
болса, АВ
көбейтіндісін
табыңыз.
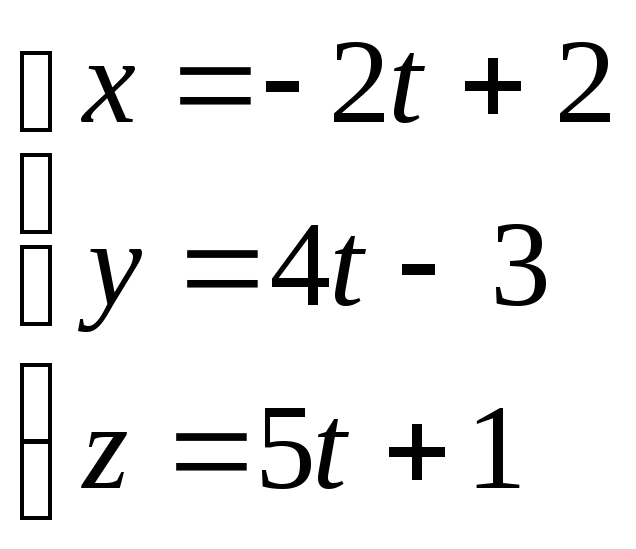
 түзуінің
бағыттауыш
векторын жазыңыз.
түзуінің
бағыттауыш
векторын жазыңыз. түзуі
мен
түзуі
мен
 түзуі
мен
Оху
жазықтығының
қиылысу
нүктесін
табыңыз.
түзуі
мен
Оху
жазықтығының
қиылысу
нүктесін
табыңыз. түзуі
мен
x+2y-z+3=0
жазықтығының
қиылысу
нүктесін
анықтаңыз.
түзуі
мен
x+2y-z+3=0
жазықтығының
қиылысу
нүктесін
анықтаңыз.
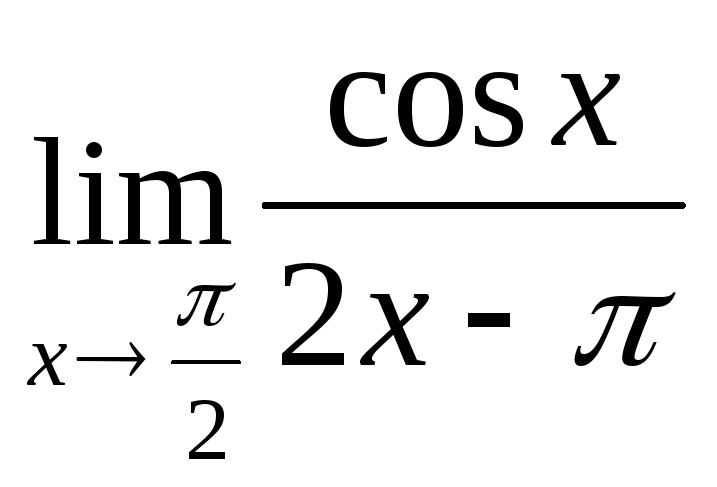





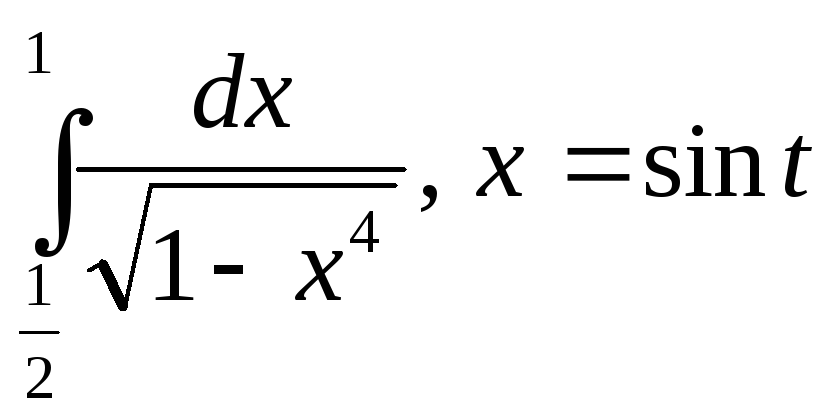





 ,
,

