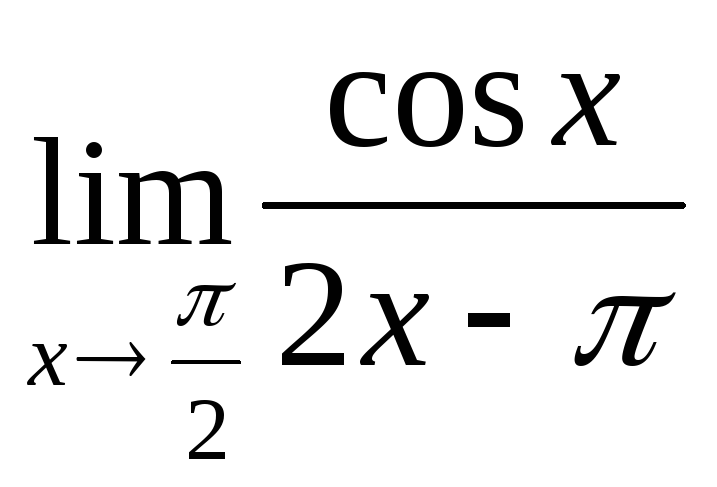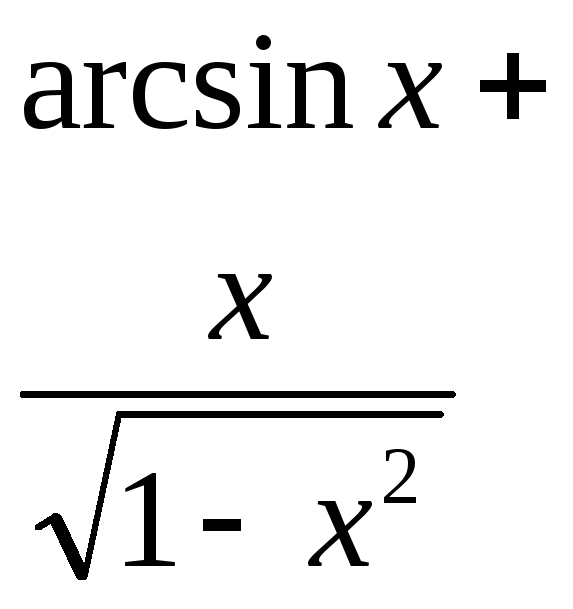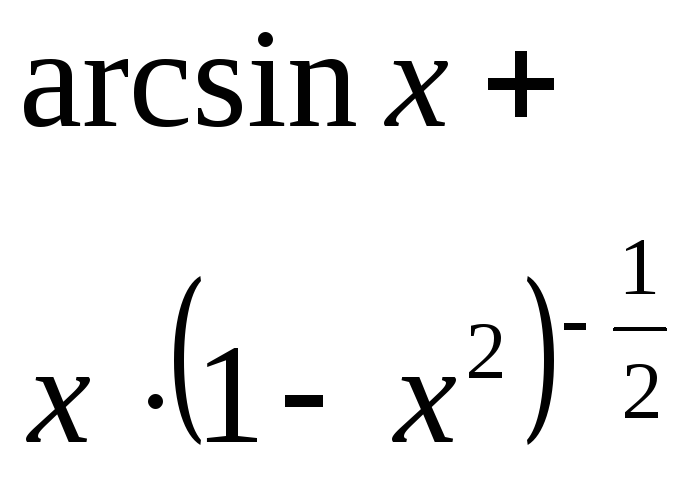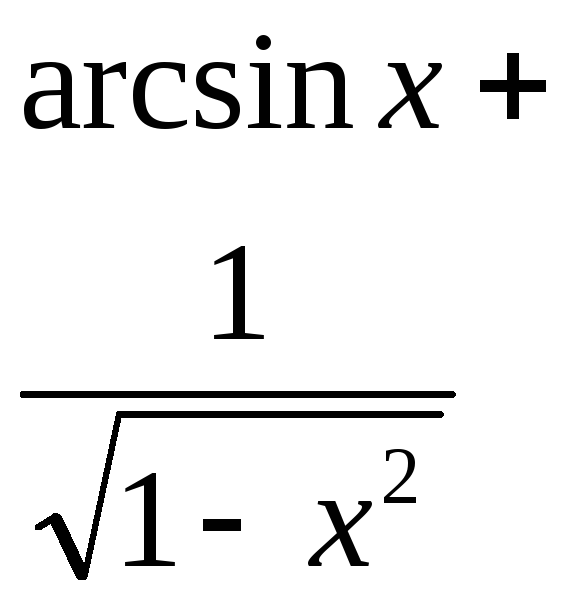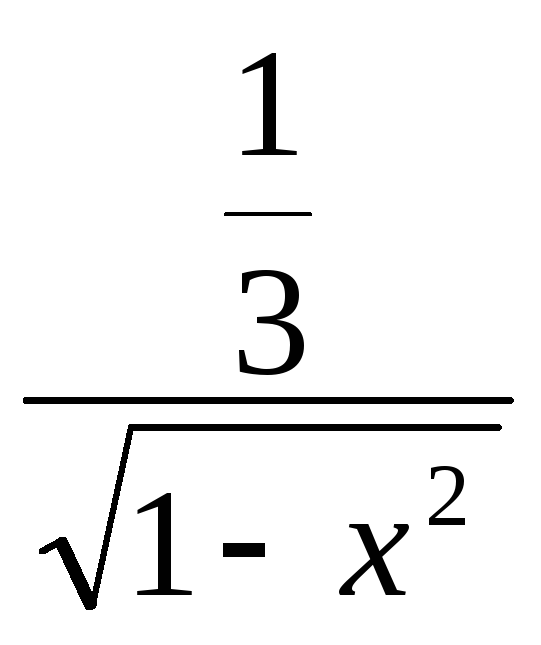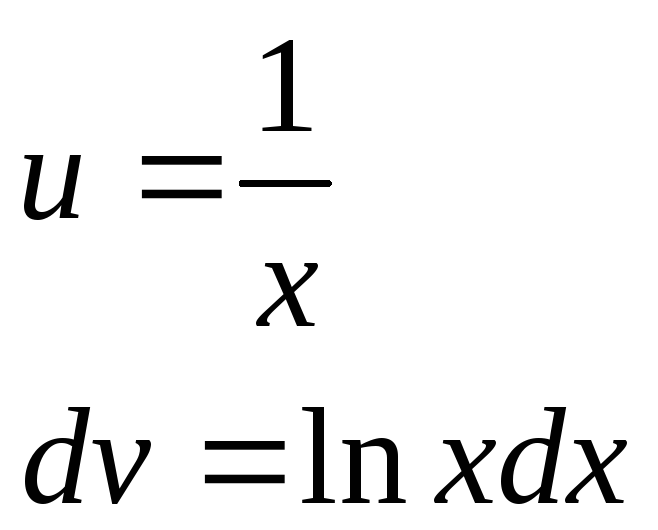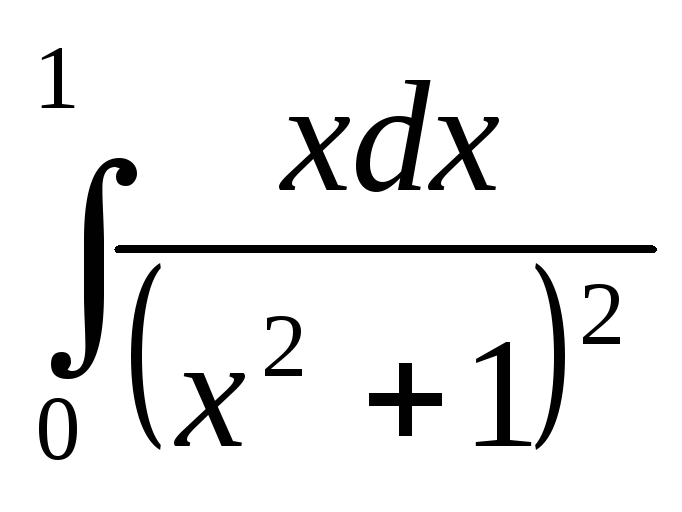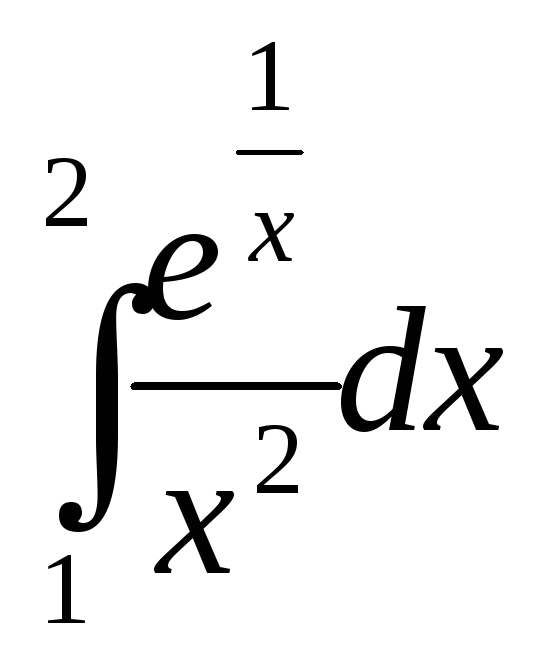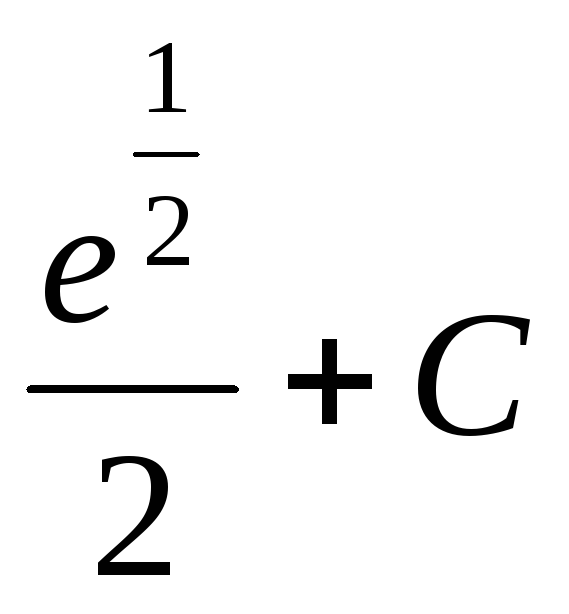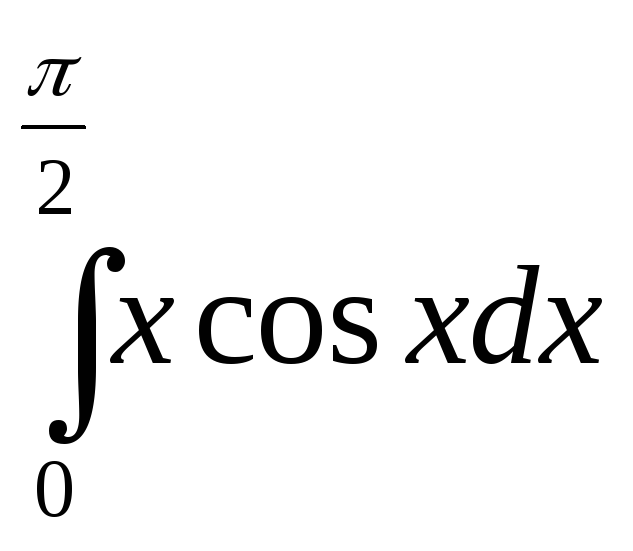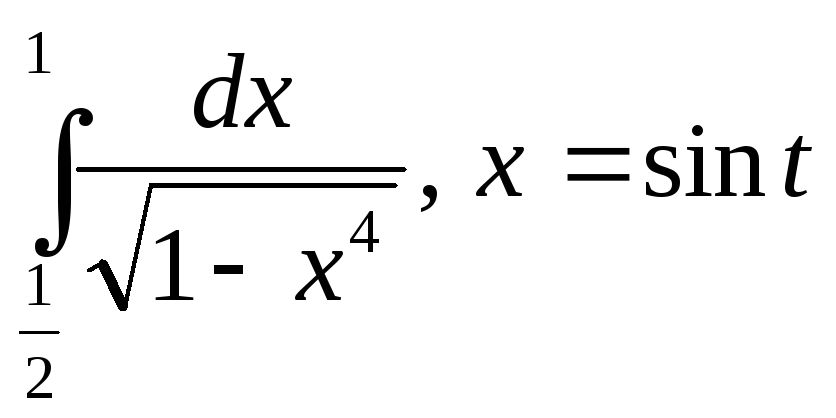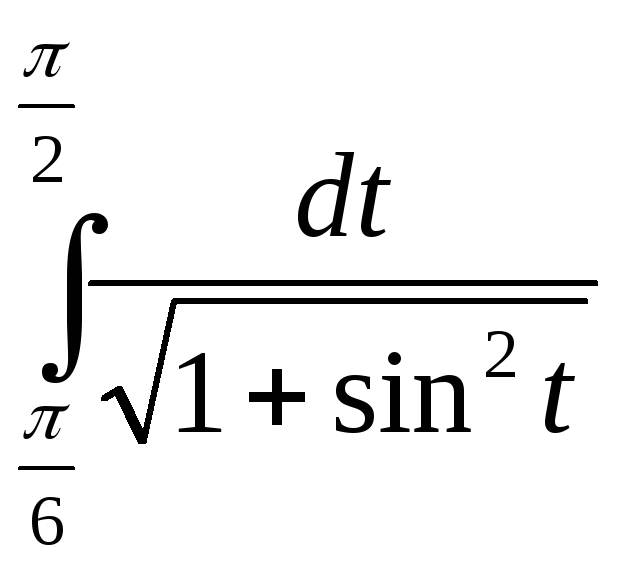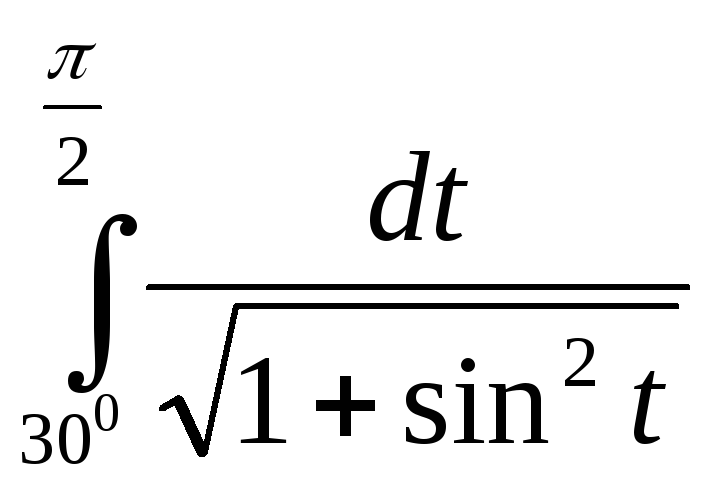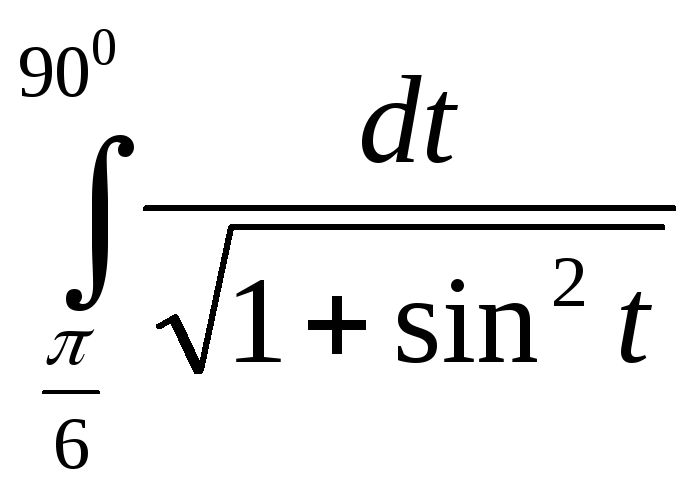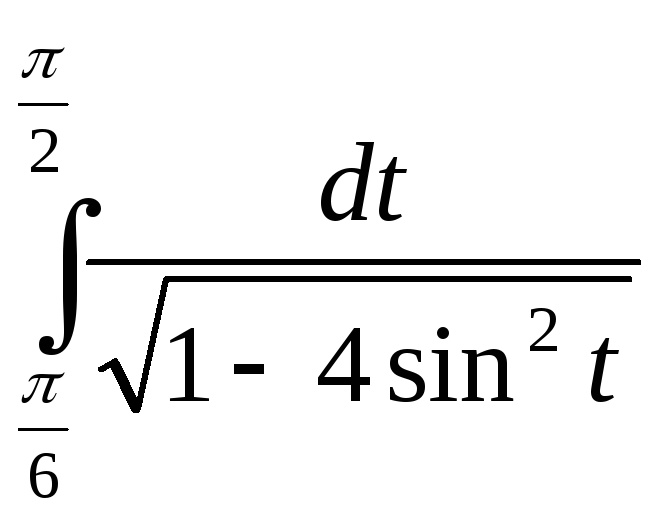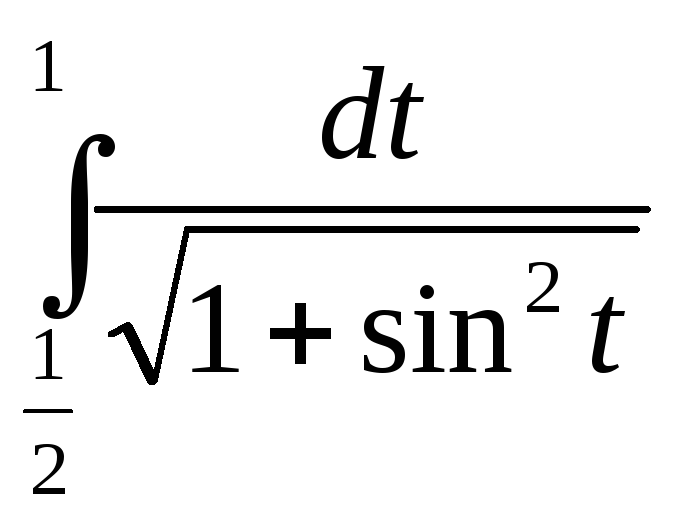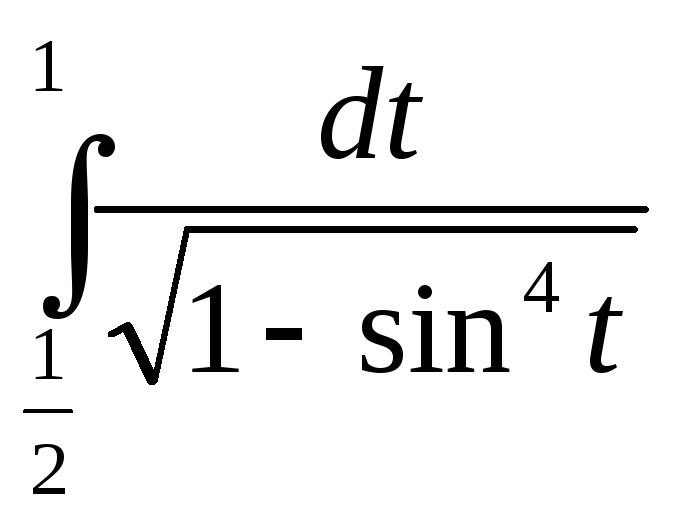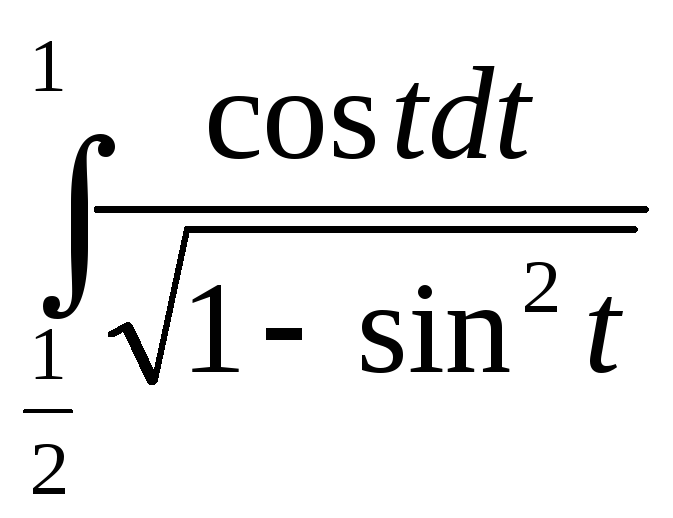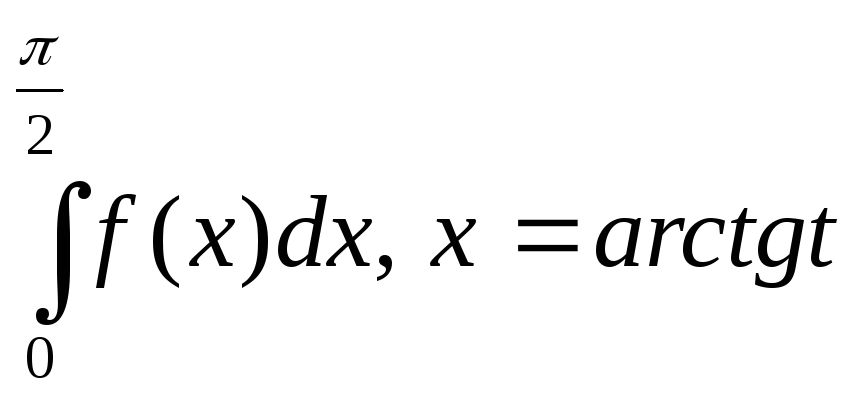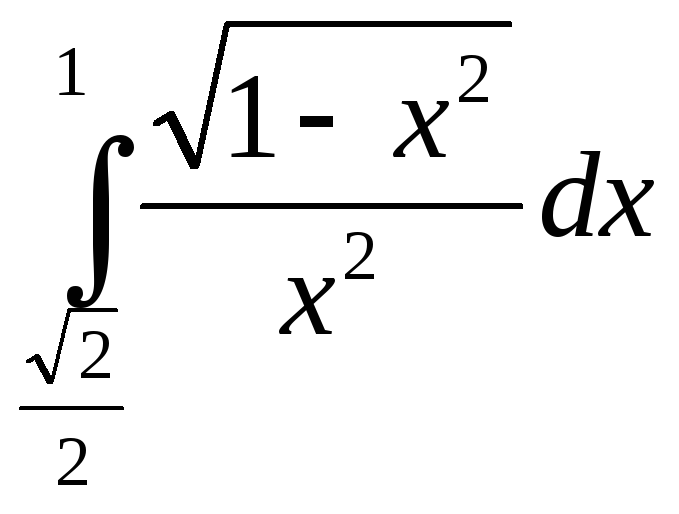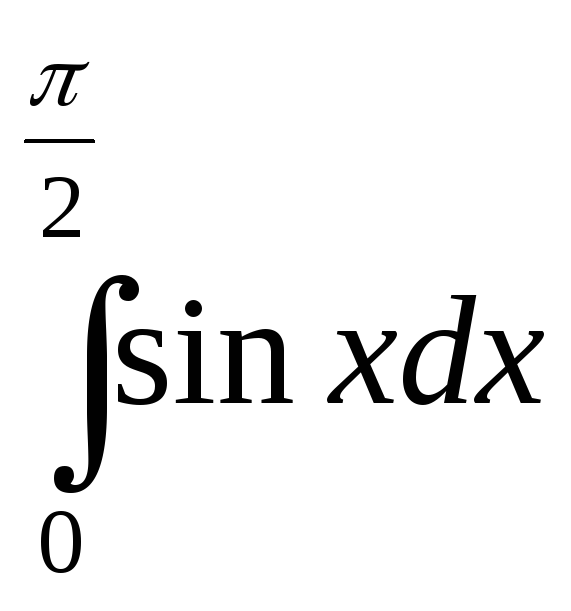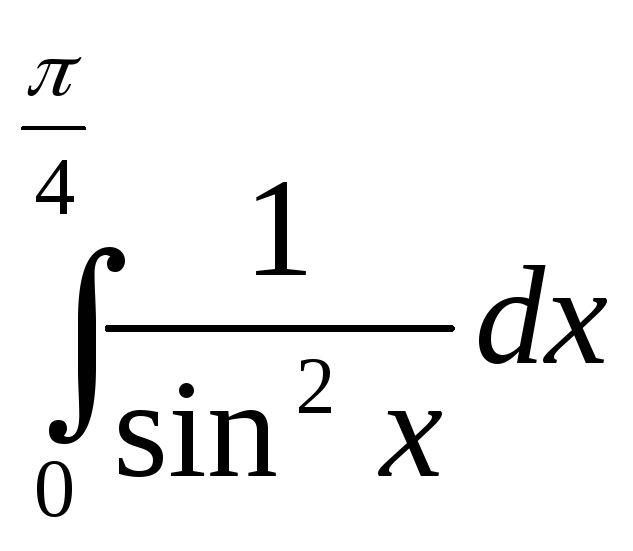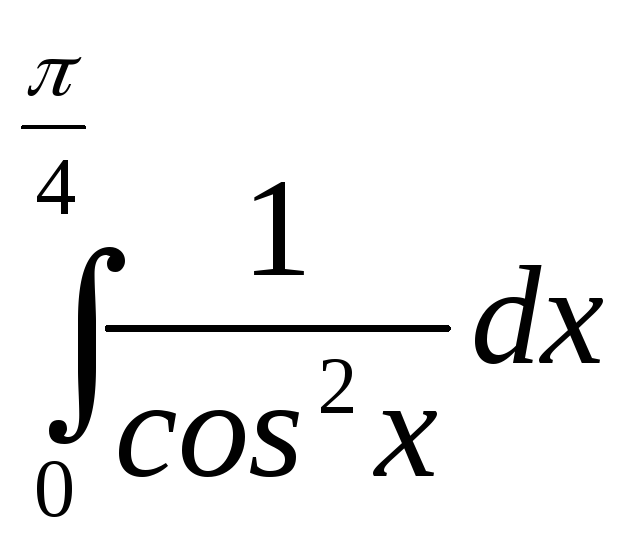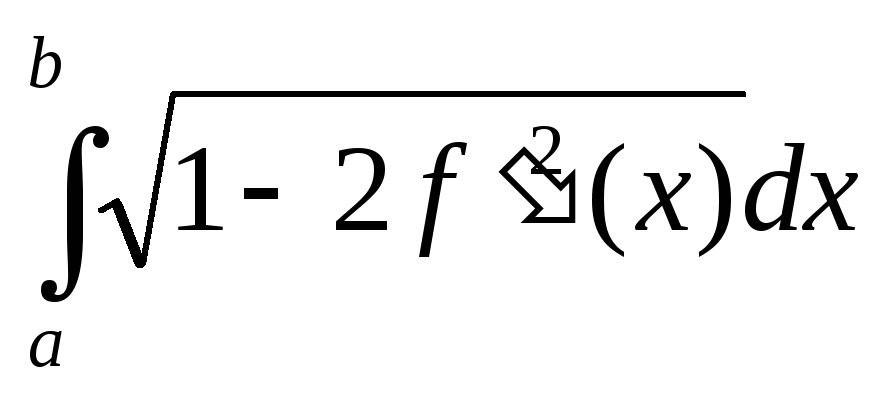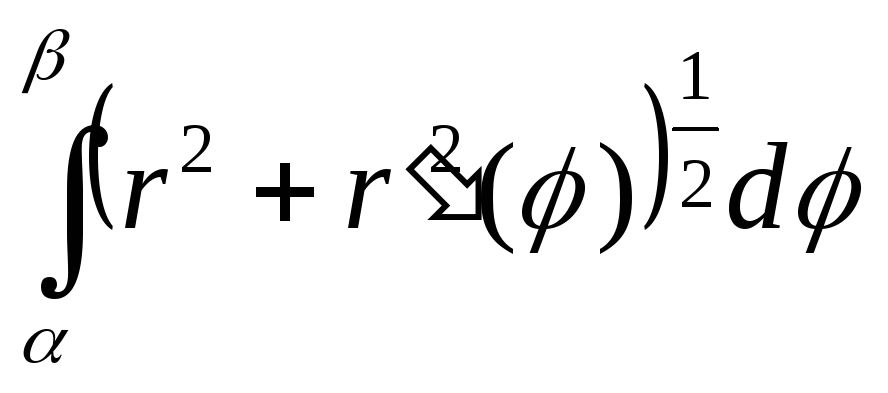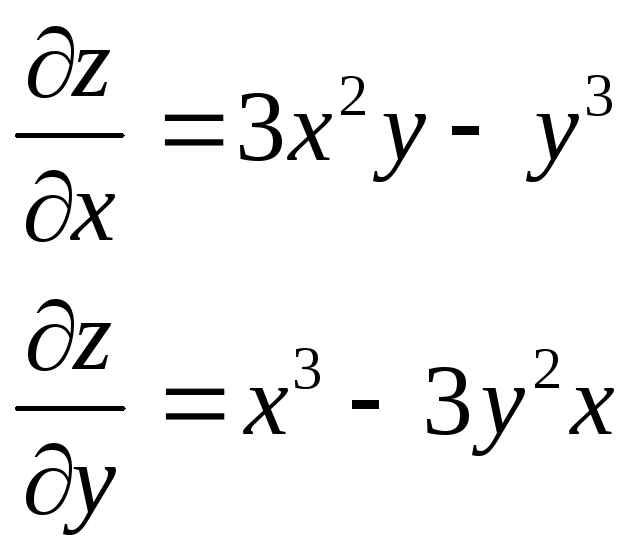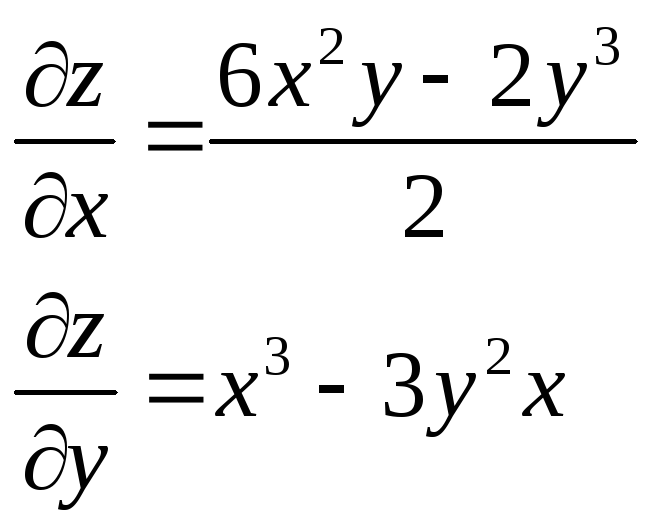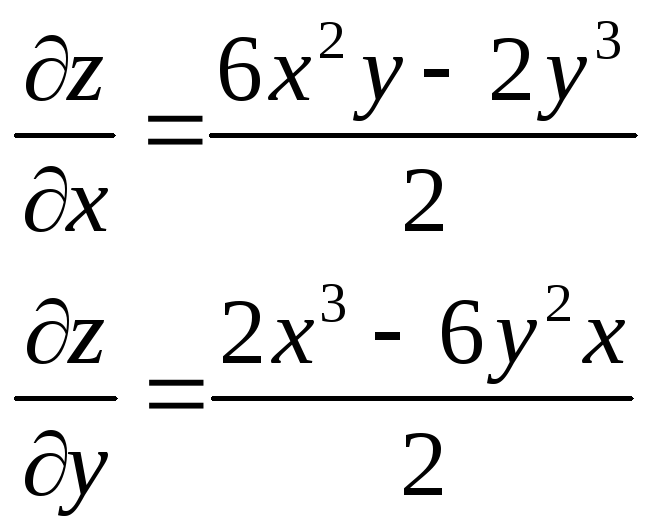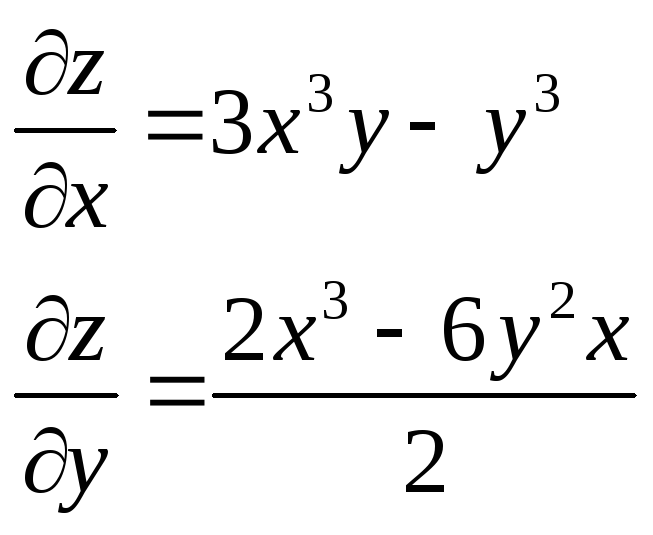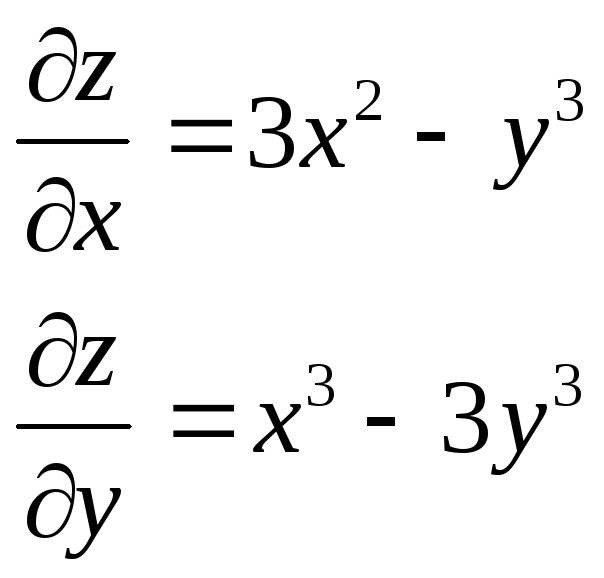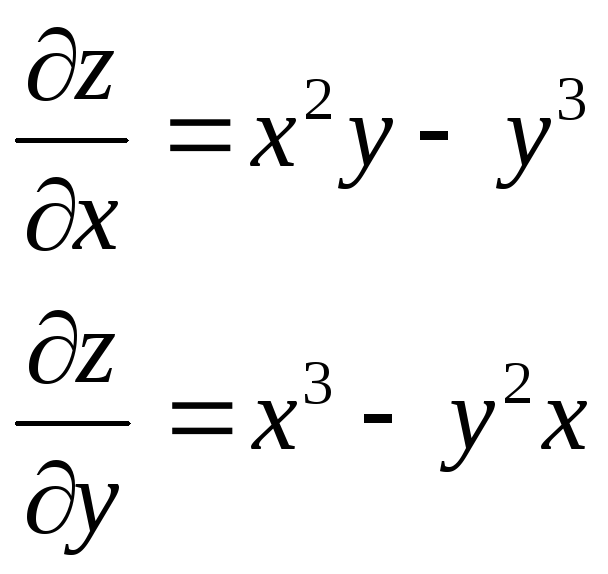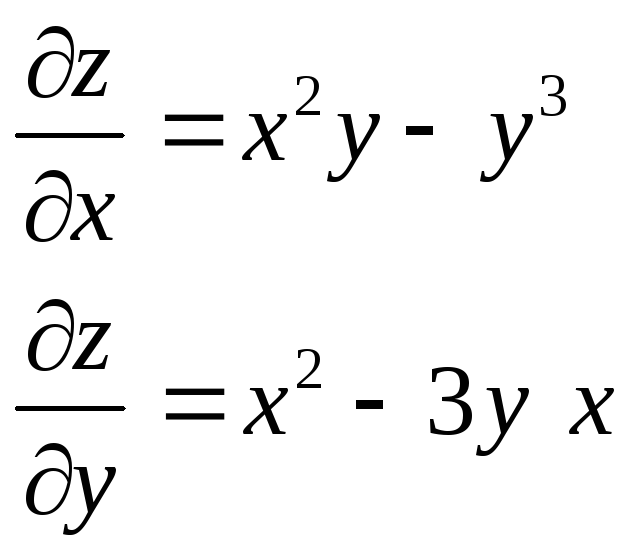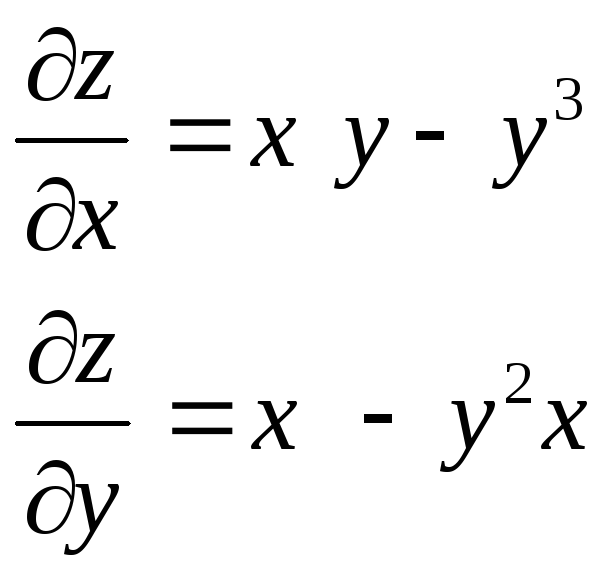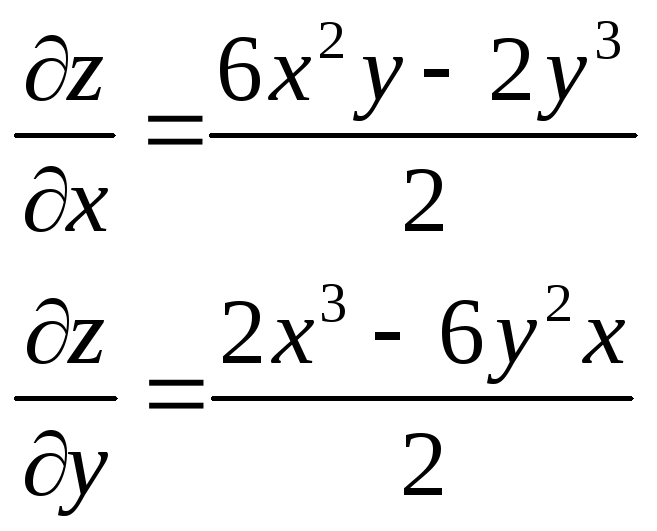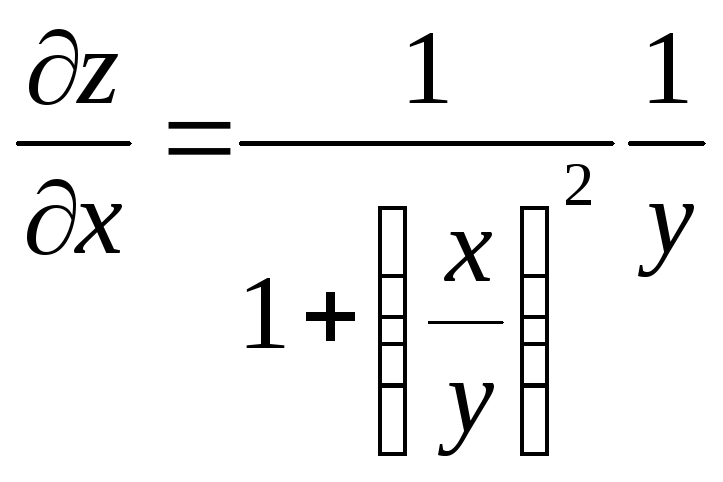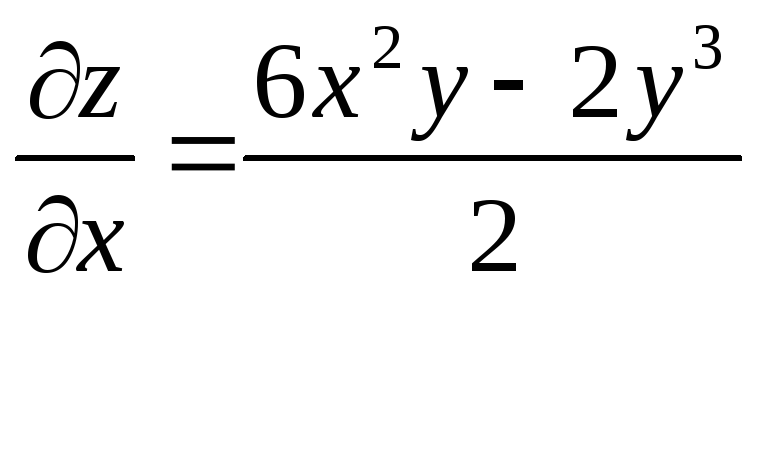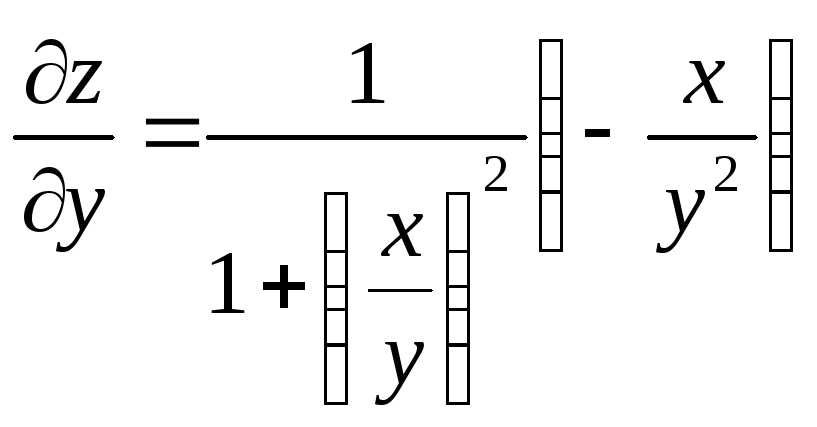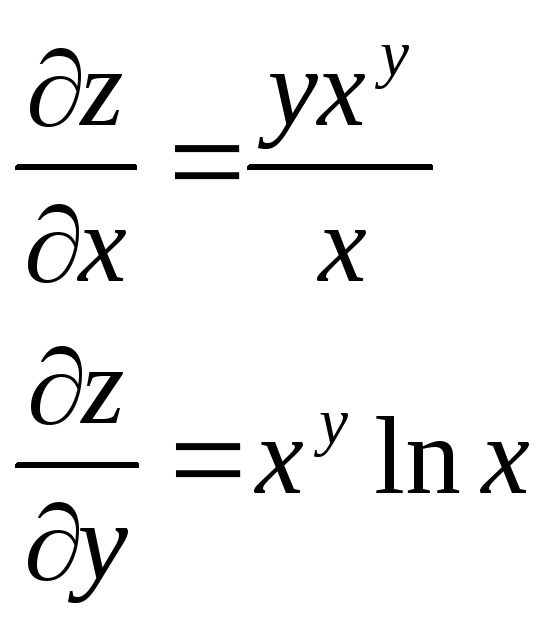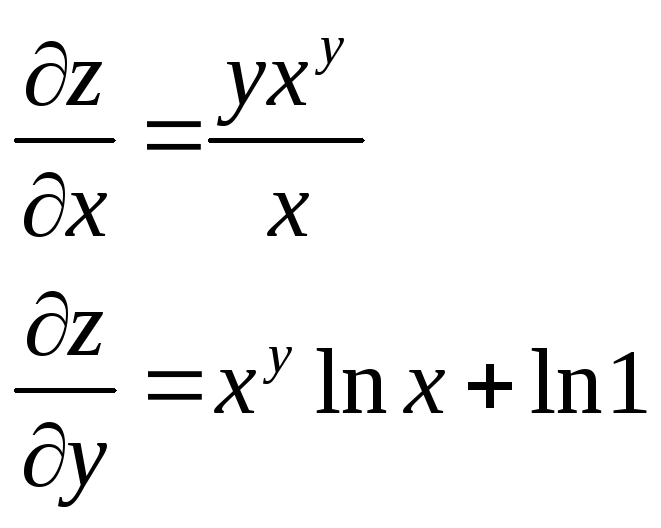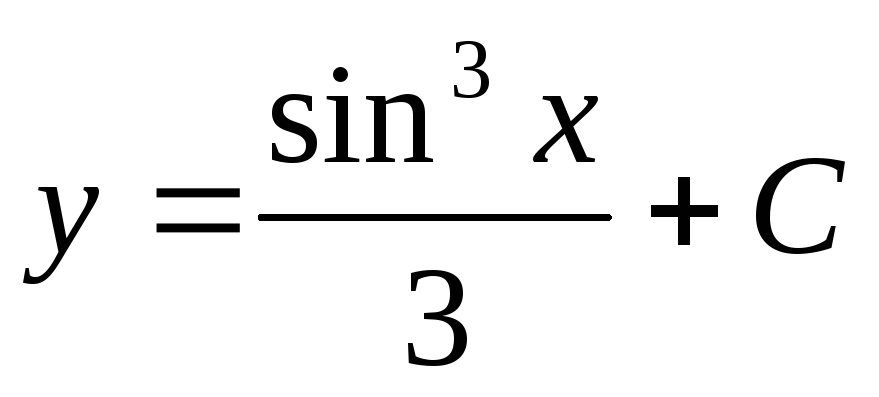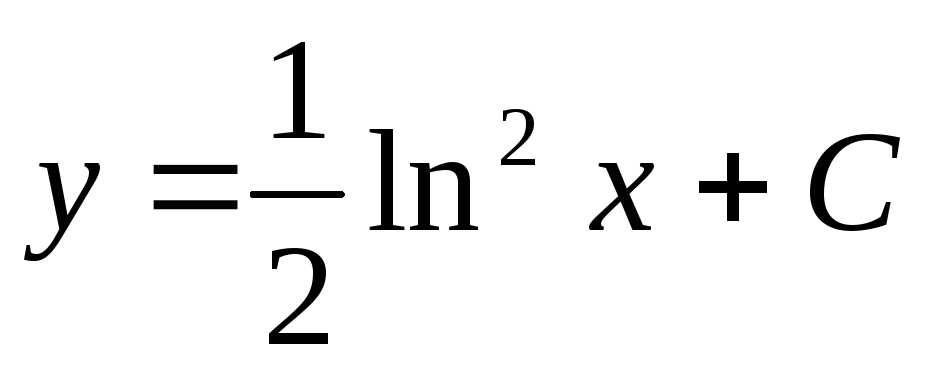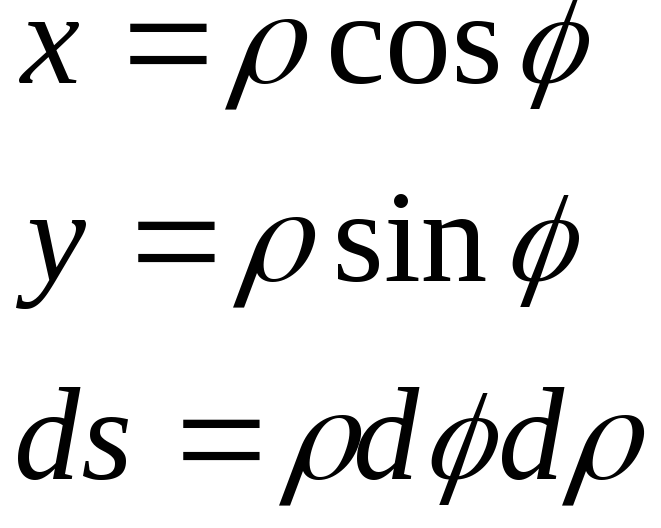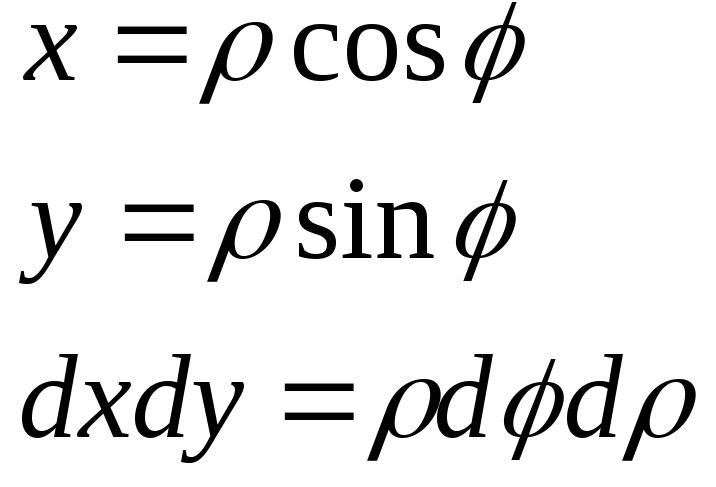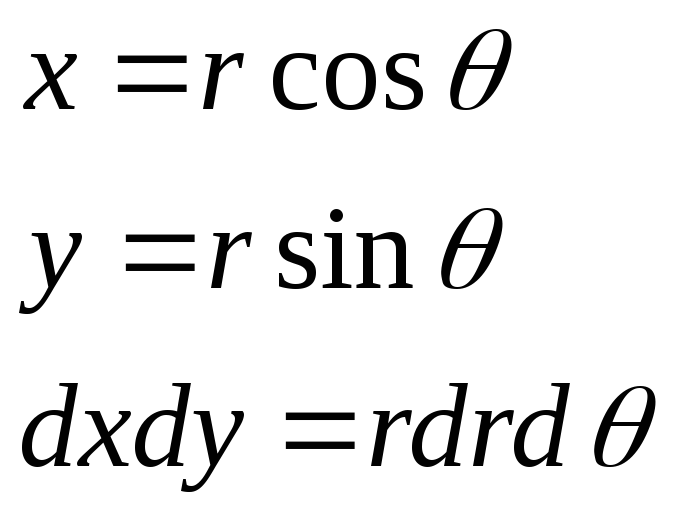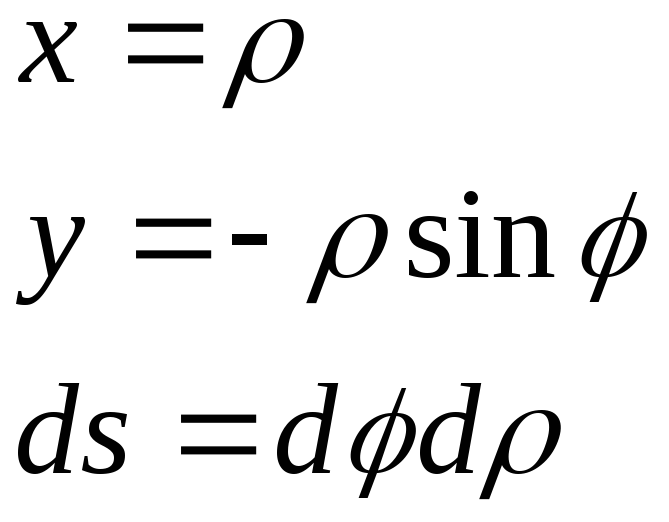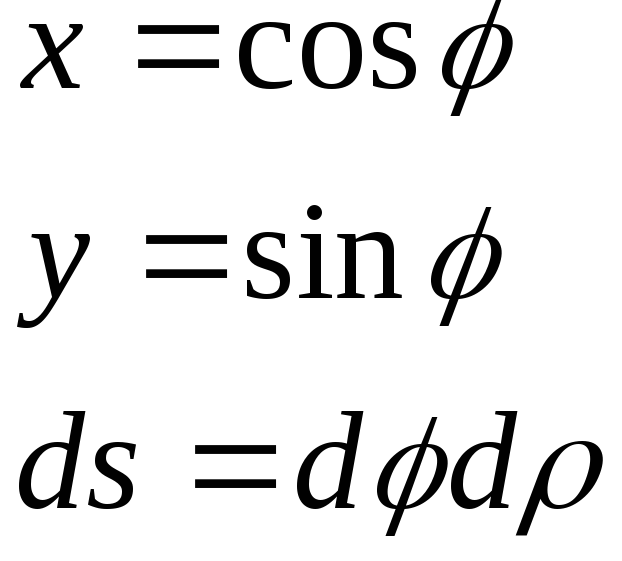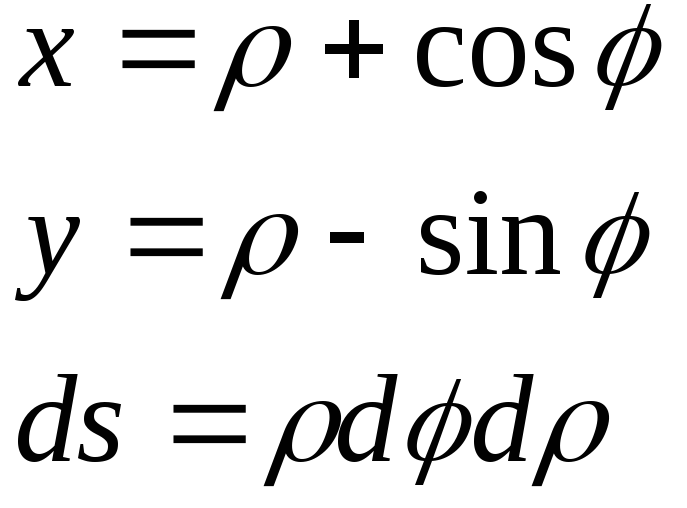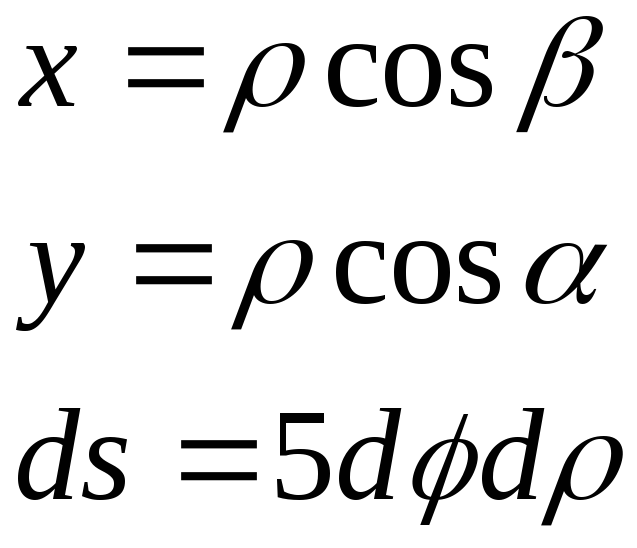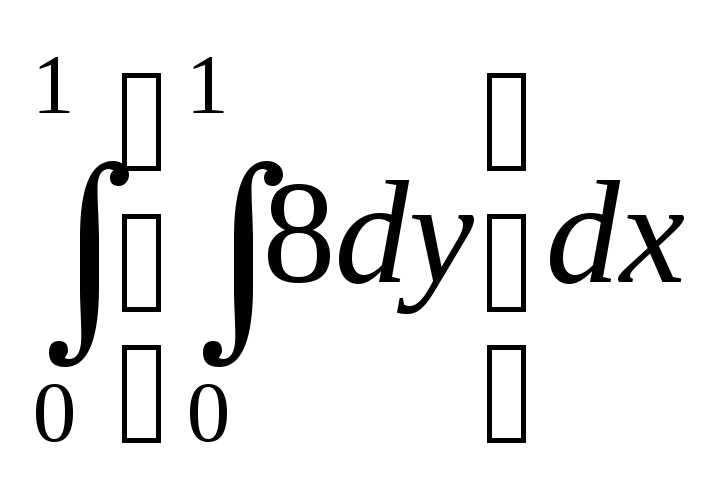математика
.doc
|
№ |
Сұрақтар |
A |
B |
C |
D |
E |
F |
G |
H |
|
|
Анықтауышты
есептеңіз
|
-1 |
(-7)*(-1)-4*2 |
7-4*2 |
(-7)*(-1)+4*2 |
2 |
7 |
0 |
-7 |
|
|
Анықтауышты
есептеңіз
|
1 |
|
|
0 |
0 |
2 |
-1 |
-2 |
|
|
Кері
матрицаны
табыңыз
|
|
|
|
|
|
|
|
|
|
|
Матрицаның
а12
элементінің
М12
минорын
есептеңіз
|
-30 |
-24-6 |
(-1)*30 |
(-1)*(-34) |
20 |
30 |
25 |
0 |
|
|
Матрицаны
транспонирлеңіз
|
|
|
|
|
|
|
|
|
|
|
Егер
А= |
|
|
|
|
|
|
|
|
|
|
Егер
А= |
|
|
3* |
|
|
|
|
|
|
|
Егер
А= |
|
|
|
|
|
|
|
|
|
|
Теңдеулер
жүйесін шешіңіз.
|
(3;1;1) |
|
|
|
(1;1;0) |
(1,1,1) |
(1;7;9) |
(2,2,2) |
|
|
Матрицаның рангысын табыңыз. А= |
2 |
|
|
|
1 |
0 |
3 |
4 |
|
|
|
(5,2) |
|
|
|
(1,1)
|
(0,2) |
(3,3) |
(5,4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
4 |
25 |
7 |
1 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
10 |
2 |
7 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
160 |
360 |
|
|
|
3 |
|
|
|
|
9 |
|
|
|
|
|
13 |
|
|
|
49 |
49/2 |
13/2 |
7 |
|
|
|
5 |
|
|
|
-5 |
10 |
0 |
6 |
|
|
Х-тің
қандай мәнінде
|
- |
- |
- |
- |
|
10 |
5 |
-7 |
|
|
y-тің
қандай мәнінде
|
-3 |
|
|
|
3 |
1 |
0 |
5 |
|
|
2х+3у-6=0 түзуі Ох осін қандай нүктеде қиып өтеді? |
(3,0) |
|
|
|
(0,0) |
(1,2) |
(4,5) |
(2,2) |
|
|
A(-1,3), B(4,-2) нүктелері арқылы өтетін түзу теңдеуін жазыңыз. |
х+y-2=0 |
х+y=2 |
y=2-х |
y=х+2 |
x-y-2=0 |
-x+y-2=0 |
х+y+2=0 |
x-y+2=0 |
|
|
у= |
2/3 |
4/6 |
10/15 |
10/3 |
1/3 |
2 |
3 |
5 |
|
|
у= |
3 |
|
|
|
4 |
5 |
2 |
1 |
|
|
Координат остерінен 3 және 5 тең кесінді қиып өтетін түзу теңдеуін жазыңыз. |
|
|
|
|
|
|
|
|
|
|
Шеткі нүктелері А(3;2) және В(12;8) нүктелері болатын түзу кесіндісі үш тең бөлікке бөлінген. Бөліну нүктелерінің координаталарын анықтаңыз. |
(6;4), (9;6) |
( (9; |
(6; |
(6;4), (9;16) |
(0;4), (0;6) |
(6;0), (0;0) |
(1;1), (2;2) |
(4;4), (0;0) |
|
|
А(-1;5) нүктесінен 4x+3y-5=0 түзуіне дейінгі қашықтықты табыңыз. |
|
|
|
- |
1 |
|
|
0 |
|
|
Берілген түзулердің қайсысы у=3х+5 түзуіне параллель а)
у= в)
у= |
в |
б |
г |
б, г |
а |
б |
в |
а, б |
|
|
Параллель түзулерді көрсетіңіз. а) 6х+у-3=0, б) х-6у-3=0, в) 12х+2у+7=0, г) 6х-у+3=0 |
а, в |
6х+у-3=0, 12х+2у+7=0, |
6х+у=3, 12х+2у=-7 |
6х-у=3+х, 12х+2у=7+у |
а, г |
б, в |
б, г |
а, б |
|
|
Перпендикуляр түзулерді көрсетіңіз. а) х+у=0, б) 10х-6у+1=0, в) у+1=0, г) 3х+5у-9=0 |
б, г |
10х-6у+1=0, 3х+5у-9=0 |
10х-6у=-1, 3х+5у=9 |
10х-1+6у=0, 3х+5у=9 |
а, в |
а, г |
б, в |
а, б |
|
|
у=-2х, у=3х+5 екі түзу арасындағы бұрышты табыңыз. |
|
|
|
|
|
|
|
|
|
|
А(1;-2), |
|
|
|
|
|
|
|
|
|
|
М(4;-7) нүктесі арқылы өтетін Оу осіне параллель түзу теңдеуін жазыңыз. |
х-4=0 |
х=4 |
х+0у-4=0 |
х+0у-7=0 |
5x-2y=0 |
x+у-1=0 |
х-у+2=0 |
х-у-5=0 |
|
|
4x+3y-5=0 түзуінің нормалаушы көбейткішін табыңыз. |
|
|
|
|
1 |
|
-1 |
|
|
|
Егер
нормальдың ұзындығы
р=3
тең, ал
оның Ох
осінің оң бағытымен жасайтын
|
|
|
|
|
|
|
|
|
|
|
а-ның қандай мәнінде (a+3)x+ay+4=0 түзуі абсцисса осіне параллель болады? |
-3 |
|
|
|
3 |
0 |
1 |
2 |
|
|
Төбелері А(3;2), В(5;-2), С(1;0) болатын АВС үшбұрышының ВМ медианасының теңдеуін жазыңыз. |
х+у-3=0 |
х+y=3 |
y=3-х |
y=х+3 |
|
|
|
|
|
|
Р(-8;12) нүктесінің А(2;-3) және В(-5;1) нүктелері арқылы өтетін түзуге түсірілген проекциясын табыңыз. |
(-12;5) |
( |
(-12; |
(12;- |
(-2;-5) |
(2;0) |
(-2;2) |
(10;11) |
|
|
х+2у-z-2=0 жазықтығының нормаль векторын көрсетіңіз. |
(1,2,-1) |
(1, |
( |
(12;- |
(1,2,3) |
(2,5,1) |
(2,-3,5) |
(1,3,8) |
|
|
|
x-2y-3z-4=0 |
x-2y-3z=4 |
х=2y+3z+4 |
x-2y-3z=9 |
х+2y-3z-6=0 |
x-2y-3z+4=0 |
х+2y+3z+4=0 |
x-2y-3z-6=0 |
|
|
|
-3y+4z+13=0 |
3y=4z+13 |
3y-4z=13 |
3y-4z=-15 |
2x+3y-z-5=0 |
3y+4z+13=0 |
2x+3y-z+5=0 |
-3y-4z-13=0 |
|
|
2x-y+3z+6=0 жазықтығының Ох осімен қиылысу нүктесін табыңыз. |
(-3;0;0) |
|
|
|
(1,0,0) |
(2,3,3) |
(4,5,6) |
(0,0,0) |
|
|
x+y+z-6=0, 3x-y+z-4=0, 2x+y-z-1=0 жазықтықтарының қиылысу нүктесін табыңыз. |
(1;2;3) |
|
|
|
(1,0,1) |
(-1,0,3) |
(4,0,-5) |
(7,8,2) |
|
|
Параллель жазықтықтарды көрсетіңіз. а) 4x-6y+3z+6=0, б) 2x-3y+z-5=0, в) x+y+z+6=0, г) 8x-12y+6z-1=0. |
а, г |
x-6y+3z+6=0, 8x-12y+6z-1=0 |
б, в –дан басқалары |
а, г –дан басқалары |
б, г |
а, в |
б, в |
а, б |
|
|
Перпендикуляр жазықтықтарды көрсетіңіз. а) 2x-y+2z+9=0, б) x-3y+z-5=0, в) x+4y+z-7=0, г) 4x-6y+3z+6=0. |
а, в |
2x-y+2z+9=0, x+4y+z-7=0, |
б,г –дан басқалары |
а, в –дан басқалары |
а, г |
б, г |
б, в |
а, б |
|
|
|
|
|
|
|
|
|
|
|
|
|
М(1;-2;4) нүктесі арқылы өтетін Охz жазықтығына параллель жазықтық теңдеуін жазыңыз. |
у+2=0 |
у=-2 |
0x+y+2=0 |
0x+y+20=0 |
7x-y-5z=0 |
2х+5=0 |
4у-8=0 |
5х+у-5=0 |
|
|
x-2y+2z-8=0, x+ -6=0 жазықтықтарының арасындағы бұрышты табыңыз. |
|
|
|
|
|
|
|
|
|
|
М1(3;-1;2), М2(4;-1;-1), М3(2;0;2) нүктелері арқылы өтетін жазықтық теңдеуін жазыңыз. |
3х+3у+z-8=0 |
3х+3у+z=8 |
3х+3у=8-z |
3х+3у=z+18 |
2х+5=0 |
4у-7=0 |
2х+3у=0 |
2х+3у-7=0 |
|
|
А(3;-1;2)
және
В(4;-2;-1)
нүетелері берілген.
А
нүктесі арқылы өтетін
|
x-у-3z+2=0 |
x-у-3z=-2 |
x-у=3z-2 |
x-3у=3z-22 |
x+4y+7z-27=0 |
x+7z-27=0 |
4x+y+7z-2=0 |
3x-7z-7=0 |
|
|
(2;3;-4) нүктесінен 2х+6у-3z+16=0 жазықтығына дейінгі қашықтықты тап. |
|
|
7,1 |
7,7 |
10 |
8 |
7 |
9 |
|
|
М(1;1;1) нүктесінен 3x+4y+7=0 жазықтығына дейінгі қашықтықты табыңыз. |
2,8 |
|
|
2,4 |
4 |
5 |
6 |
7 |
|
|
x-y+z-1=0, 2x-2y+2z-5=0 параллель жазықтықтарының ара қашықтықтарын табыңыз. |
|
|
|
|
1 |
2 |
3 |
5 |
|
|
Координат остерінің x+2y+4z-4=0 жазықтығымен қиғандағы кесінділерін тап. |
а=4, в=2, с=1 |
в=2, а=4, с=1 |
с=1, а=4, в=2 |
в=2, а=0,с=1 |
а=1, в=1, с=1 |
а=2, в=2, с=2 |
а=4, в=4, с=2 |
а=3, в=2, с=1 |
|
|
2x+3y-8z-24=0 жазықтығының теңдеуі берілген. Жазықтықтың кесіндідегі теңдеуін жаз. |
|
|
|
|
|
|
|
|
|
|
2х-2у+z-18=0 жазықтығының нормалаушы көбейткішін табыңыз. |
|
|
|
|
10 |
2 |
4 |
9 |
|
|
3x+2y+6z-4=0 жазықтығының нормальдық теңдеуін жазыңыз. |
|
|
|
|
x+ |
|
|
|
|
|
A(1,2,3), B(2,4,6) нүктелері арқылы өтетін түзудің теңдеуін жазу керек. |
|
|
|
|
|
|
|
|
|
|
A(-1,2,3), B(2,6,-2) нүктелері арқылы өтетін түзу теңдеуін жазыңыз. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М(2;-3;1)
нүктесі арқылы өтетін
|
|
|
|
|
|
|
|
|
|
|
А(-2,1,-1)
нүктесі
арқылы өтетін
|
|
|
|
|
|
|
|
|
|
|
М(2;-3;-5) нүктесі арқылы өтетін 6x-3y-5z+2=0 жазықтығына перпендикуляр түзу теңдеуін жазыңыз. |
|
|
|
|
|
|
|
|
|
|
М(2;0;3)
нүктесі арқылы өтетін
|
3x+6y+2z-12=0 |
3(х-2)+6у+2(z-3)=0 |
3х+6у+2z-6-6=0 |
3(х-2)+6у=0 |
2x-3y+4z-1=0 |
3х+у-5=0 |
2х-у+z=0 |
2x-3z=0 |
|
|
|
|
|
x=-1, y=-7, z=-5 |
x=1, y=7, z=8 |
|
|
|
|
|
|
2x-y+z+3=0 жазықтығының арасындағы бұрышын табыңыз. |
|
|
|
|
|
|
|
|
|
|
|
-
|
- |
- |
|
|
|
|
|
|
|
|
(4;-5;1) |
x=4, y=-5, z=1 |
x=4, z=1, y=-5 |
x=4, y=-5, z=0 |
(1,0,1) |
(1,2,4) |
(2,4,4) |
(-1,-2,3) |
|
|
|
(3;-3;0) |
x=3, y=-3, z=0 |
x= |
x= |
(1,0,1) |
(1,2,4) |
(2,4,4) |
(-1,-2,3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Шеңбердің
теңдеуін құрыңыз, егер ол координаттар
бас нүктесі арқылы өтетін және оның
центрі
|
|
|
|
|
|
|
|
|
|
|
Эллипстің
теңдеуін құрыңыз, егер оның жарты
остері
|
|
|
|
|
|
|
|
|
|
|
Эллипстің канондық теңдеуін құрыңыз. |
|
|
|
|
|
|
|
|
|
|
Шеңбердің канондық теңдеуін табыңыз. |
|
|
|
|
|
|
|
|
|
|
Эллипстің
теңдеуін құрыңыз, егер оның жарты
остері
|
|
|
|
|
|
|
|
|
|
|
Шекті
есептеңіз:
|
-16 |
-32/2 |
|
|
10 |
12 |
0 |
5 |
|
|
Шекті
есептеңіз:
|
1 |
|
|
|
2 |
3 |
4 |
5 |
|
|
Шекті
есептеңіз:
|
|
|
Шексіздік |
|
1 |
2 |
0 |
5 |
|
|
Шекті
есептеңіз:
|
-2/3 |
|
-0,6(6) |
0,4(4) |
1/3 |
5/3 |
4/3 |
8/3 |
|
|
Шекті
есептеңіз:
|
1/3 |
|
0,3(3) |
0,4(4) |
1/5 |
1/6 |
1/7 |
1/8 |
|
|
Шекті
есептеңіз:
|
2 |
|
|
|
1 |
0 |
3 |
4 |
|
|
Шекті есептеңіз:
|
|
|
|
|
0 |
1 |
-1 |
2 |
|
|
Шекті
есептеңіз:
|
4/5 |
|
|
|
1/5 |
2/5 |
3/5 |
6/5 |
|
|
Шекті
есептеңіз:
|
|
|
0,3(3) |
0,4(4) |
3 |
1 |
0 |
|
|
|
Шекті
есептеңіз:
|
-1/2 |
|
|
|
0 |
1/4 |
1/2 |
1 |
|
|
Шекті
есептеңіз:
|
0 |
|
|
|
1 |
1/2 |
-1 |
|
|
|
Шекті
есептеңіз:
|
|
|
|
|
e |
|
0 |
1 |
|
|
Шекті
есептеңіз:
|
|
|
|
|
е |
е+1 |
0 |
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
0 |
|
|
|
-1 |
1 |
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
0 |
1 |
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
0 |
|
|
1 |
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны
табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны табыңыз:
|
|
|
|
|
|
|
|
|
|
|
Туындыны
табыңыз
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Туындыны
табыңыз
|
0 |
|
|
|
|
- |
1 |
|
|
|
Туындыны
табыңыз
|
|
|
|
|
|
|
|
4 |
|
|
Туындыны табыңыз
|
|
|
|
|
|
|
|
|
|
|
Егер
|
2 |
|
|
|
1 |
0 |
|
3 |
|
|
Егер
|
2,5 |
|
|
|
1,5 |
1 |
2 |
-1 |
|
|
Егер
|
|
|
|
|
|
|
|
3 |
|
|
|
|
(0;0), (2;4) |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
-1 |
2 |
3 |
|
|
|
6 |
|
|
|
0 |
1 |
-6 |
2 |
|
|
|
-4 |
- |
|
|
1 |
4 |
6 |
-2 |
|
|
Табу
керек:
|
1 |
|
|
|
-1 |
0 |
2 |
-2 |
|
|
Табу
керек:
|
1 |
|
|
|
-1 |
0 |
2 |
-2 |
|
|
Қандай нүктелерде кубтық параболаның бұрыштық коэффициенті 3-ке тең? |
(1,1) және (-1,-1) |
|
(-1,-1) және(1,1) |
|
(1,1) |
(-1,-1) |
(0,0) |
(0,0) және (1,1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Материалдық
нүктенің қозғалысының теңдеуі берілген:
|
26 |
|
|
|
15 |
16 |
20 |
14 |
|
|
|
-1 |
- |
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Табу
керек:
|
|
3,14 |
пи |
2,8 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(- |
(- |
|
(- |
(- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нолден плюс шексіздікке дейін |
Минус шексіздіктен нолге дейін |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Есептеңіз:
|
-1 |
- |
|
|
0 |
2 |
1 |
5 |
|
|
Есептеңіз:
|
|
- |
|
|
1 |
0 |
-1 |
2 |
|
|
Есептеңіз:
|
-8 |
- |
8 |
|
|
-1 |
1 |
0 |
|
|
Есептеңіз:
|
2 |
|
|
|
-1 |
0 |
-8 |
|
|
|
Есептеңіз:
|
|
|
|
|
|
|
|
|
|
|
-
|
|
|
|
|
|
|
|
|
|
|
Есептеңіз:
|
5 |
|
|
|
-1 |
0 |
-8 |
|
|
|
Есептеңіз:
|
1 |
|
- |
|
0 |
2 |
1,5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
2x+C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегралды есептеңіз.
|
|
|
|
|
|
|
|
|
|
|
Интеграл
астындағы өрнекті қарапайым бөлшектер
қосындысына жіктеңіз |
|
|
|
|
|
|
|
|
|
|
Анықталмаған интеграл үшін бөлшектеп интегралдау формуласы. |
|
|
|
|
|
|
|
|
|
|
Интегралды
есептеңіз
|
|
|
|
|
|
|
1 |
0 |
|
|
Интегралды
есептеңіз
|
|
|
0,25 |
0,4 |
1 |
2 |
|
|
|
|
Интегралды
есептеңіз
|
|
|
|
|
|
|
0 |
|
|
|
Интегралды есептеңіз
|
|
|
|
|
|
|
|
|
|
|
Меншіксіз
интегралды есептеңіз
|
|
0,3(3) |
|
0,6(6) |
1 |
0 |
жинақсыз |
|
|
|
Меншіксіз
интегралды есептеңіз
|
жинақсыз |
|
|
7 |
1 |
0 |
|
|
|
|
Интегралды
есептеңіз
|
|
|
|
|
|
0 |
1 |
2 |
|
|
Интегралды
есептеңіз
|
жинақсыз |
|
|
7 |
-1 |
0 |
|
|
|
|
Интегралды
есептеңіз
|
2 |
|
|
|
1 |
0 |
жинақсыз |
|
|
|
Берілген
алмастыру арқылы анықталған интегралды
түрлендіріңіз |
|
|
|
|
|
|
|
|
|
|
Берілген
алмастыру арқылы анықталған интегралды
түрлендіріңіз
|
|
|
|
|
|
|
|
|
|
|
Берілген
алмастыру арқылы анықталған интегралды
түрлендіріңіз
|
|
|
|
|
|
|
|
|
|
|
Берілген
алмастыру арқылы анықталған интегралды
түрлендіріңіз
|
|
|
|
|
|
|
|
|
|
|
Берілген
алмастыру арқылы анықталған интегралды
түрлендіріңіз
|
|
|
|
|
|
|
|
|
|
|
Қандай алмастыру қолдануға болады
|
|
|
|
|
|
|
|
|
|
|
Теңдеуді шешіңіз
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
5 |
|
|
|
Интегралды есептеңіз
|
|
|
|
|
|
|
|
|
|
|
Берілген аралықтағы функцияның орта мәнін табыңыз
|
|
0,3(3) |
|
8 |
2 |
1 |
|
- |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
2 |
|
|
|
1 |
0 |
5 |
|
|
|
|
1 |
|
|
|
|
|
5 |
|
|
|
|
-1 |
- |
- |
|
|
|
5 |
|
|
|
|
1 |
|
|
|
|
|
5 |
|
|
|
Шектері бірдей анықталған интегралдың мәні неге тең? |
0 |
|
|
8 |
1 |
Интегралдың жоғарғы шегіне |
Интегралдың төменгі шегіне |
2 |
|
|
|
|
0,3(3) |
|
8 |
5 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
4,5 |
|
4,8 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
15 |
1 |
|
|
Декарттық координат жүйесіндегі доғаның ұзындығының формуласы. |
|
|
|
|
|
|
|
|
|
|
Параметрлік теңдеумен берілген доғаның ұзындығы. |
|
|
|
|
|
|
|
|
|
|
Поляр координаталарымен берілген доғаның ұзындығы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
4,3(3) |
|
5 |
0 |
|
|
|
|
|
|
|
10,6(6) |
|
5 |
0 |
|
|
|
|
|
|
|
|
|
|
жинақсыз |
5 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z= |
|
|
|
|
|
|
|
|
|
|
z=
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функциясының
(2;1) нүктесіндегі
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
0 |
|
|
8 |
1 |
-1 |
2 |
-2 |
|
|
Бірінші ретті біртекті дифференциалдық теңдеуді шешу үшін қандай алмастыруды пайдаланады? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференциалдық
теңдеуді шешіңіз:
|
|
|
|
|
|
|
|
|
|
|
Дифференциалдық
теңдеуді шешіңіз:
|
|
|
|
|
|
|
|
|
|
|
Дифференциалдық
теңдеуді шешіңіз:
|
|
|
|
|
|
|
|
|
|
|
Дифференциалдық теңдеуді шешіңіз:
|
|
|
|
|
|
|
|
|
|
|
Дифференциалдық
теңдеуді шешіңіз:
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
5 |
2 |
1 |
0 |
4 |
|
|
Дифференциалдық
теңдеуді шешіңіз:
|
|
|
|
|
|
|
|
|
|
|
Дифференциалдық
теңдеуді шешіңіз:
|
|
|
|
|
|
|
|
|
|
|
Дифференциалдық
теңдеуді шешіңіз:
|
|
|
|
|
|
|
|
|
|
|
Дифференциалдық
теңдеуді шешіңіз:
|
|
|
|
|
|
|
|
|
|
|
Дифференциалдық
теңдеуді шешіңіз:
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
5 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Екі еселі интеграл арқылы жазық фигураның ауданын табу формуласы. |
|
|
|
|
|
dxdydz |
x=0,y=0,z=0 |
|
|
|
Екі еселі интегралда полярлық координатаға көшу. |
|
|
|
|
|
|
|
|
|
|
Екі еселі интеграл арқылы дененің көлемін табу формуласы.
|
|
|
|
|
dxdydz |
|
|
|
|
|
Интегралдың
геометриялық мәні
|
|
Фигураның ауданы |
Жазық фигурасының ауданы |
|
|
|
|
|
|
|
|
8 |
|
|
3 |
1 |
4 |
5 |
2 |
|
|
|
|
0,5 |
|
1 |
3 |
4 |
8 |
10 |
|
|
|
|
|
|
3 |
5 |
2 |
8 |
1 |
|
|
|
|
|
|
4 |
5 |
2 |
8 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
Цилиндрлік координаталар жүйесінде М(x,y,z) нүктесінің координаталары қалай анықталады. |
x= |
x=
|
x=
|
x= |
x= |
x= |
x= |
x= |
|
|
Үш еселі интеграл арқылы дененің көлемі қалай анықталады? |
|
|
|
|
|
|
|
|
|
|
Сфералық координаталар жүйесінде М(x,y,z) нүктесінің координаталары қалай анықталады. |
x= |
x=
|
x=
|
x=
|
x= |
x= |
x= |
x= |
|
|
Интегралдың
геометриялық мәні
|
|
көлем |
Дененің көлемі |
|
|
|
S |
Инерция моменті |
|
|
Цилиндрлік координаталар жүйесінде көлем элементі. |
dV= |
dxdydz= |
dV= |
|
dV= |
dV=4 |
dV= |
dV= |
|
|
Сфералық координаталар жүйесінде көлем элементі. |
dV= |
dxdydz= |
dV= |
|
dV= |
dV= |
dV= |
dV= |
|
|
Үштік интеграл арқылы дененің көлемін қалй есептейміз? |
|
|
|
|
|
|
|
|
|
|
|
Дененің көлемі |
|
Көлем |
|
Дененің массасы |
Фигураның ауданы |
Инерция моменті |
Пластинканың ауырлық центрінің координата лары. |
|
|
|
4 |
|
|
3 |
-1/5 |
4/9 |
1,8 |
9/10 |
|
|
|
|
3,2 |
|
3 |
-1/5 |
4/9 |
1,8 |
9/10 |
|
|
T: |
|
0,0125 |
|
3 |
15 |
4,8 |
1/78 |
114 |
|
|
|
|
0,16(6)
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Қай қатар үшін жинақтылықтың қажетті шарты орындалған |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Қандай оқиға ақиқат деп аталады? |
Міндетті түрде орындалатын оқиға. |
әруақытта орындалатын оқиға |
Ықтималдығы 1-ге тең оқиға |
Ықтималдығы 2-ге тең оқиға |
Қолайлы жағдайлар дың болуына қарамастан орындалмайтын оқиғаларды |
Пайда болуыда мүмкін, пайда болмауыда мүмкін |
Тәжірибе нәтижесі… |
Кез келген нәтиже |
|
|
Қандай оқиға мүмкін емес деп аталады? |
Қолайлы жағдайлар дың болуына қарамастан орындалмайтын оқиғаларды |
Ешуақытта орындалмайтын оқиға |
Ықтималдығы 0-ге тең оқиға |
Ықтималдығы 1-ге тең оқиға |
Міндетті түрде орындалатын оқиға. |
Пайда болуыда мүмкін, пайда болмауыда мүмкін |
Тәжірибе нәтижесі… |
Кез келген нәтиже |
|
|
Қандай оқиға кездейсоқ деп аталады |
Тәжірибе нәтижесінде пайда болуыда мүмкін, пайда болмауыда мүмкін. |
Орындалуы да орындалмауы да мүмкін оқиға |
Ықтималдығы 0-мен 1-дің арасындағы оқиға |
Ықтималдығы 1-ге тең оқиға |
Қолайлы жағдайлар дың болуына қарамастан орындалмайтын оқиғаларды. |
Міндетті түрде орындалатын оқиға. |
Тәжірибе нәтижесі… |
Кез келген нәтиже |
|
|
Ықтималдықтың класикалық анықтамасы? |
Р(А)=m/n |
Р(А)= |
Р(А)=m*n-1 |
Р(А)=m |
W(A)=m/n |
A |
C |
P |
|
|
Салыстырмалы жиілігі есептелетін формуланы көрсетіңіз: |
W(A)=m/n |
W(А)= |
W(А)=m*n-1 |
W(А)=m |
Р(А)=m/n |
A |
C |
P |
|
|
Ақиқат оқиғаның ықтималдығы неге тен? |
1 |
lne |
50 |
6 |
0 |
|
2 |
0,1 |
|
|
Мүмкін емес оқиғаның ықтималдығы неге тен? |
0 |
lne |
50 |
6 |
1 |
|
2 |
0,1 |
|
|
Кездейсоқ оқиғанын ықтималдығы Р(А) теңсіздікті қанағаттандырады…: |
|
|
|
|
|
|
|
|
|
|
n элементтен жасалатын алмастыру есептелетін формуласын табыңдар: |
P |
P |
P |
P |
A |
C |
C |
P |
|
|
n элементтен k-дан жасалған терулер есептелетін формуласын табыңдар: |
|
|
|
|
A |
C |
C |
P |

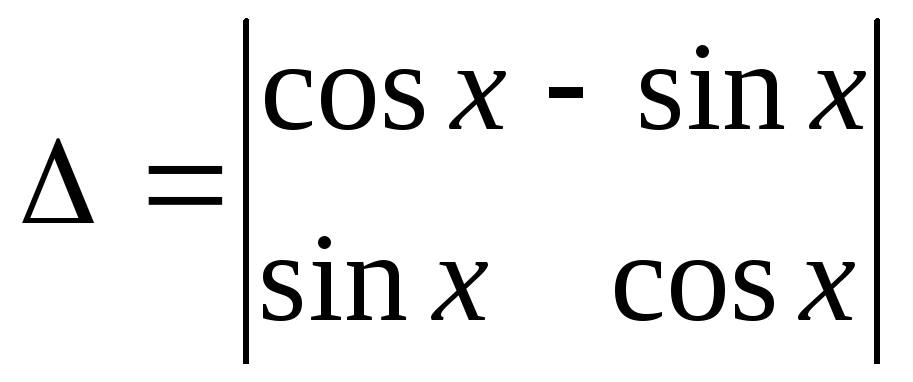
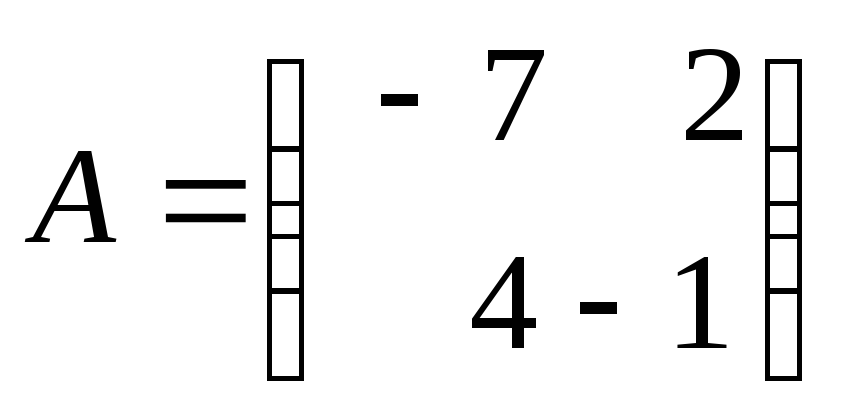
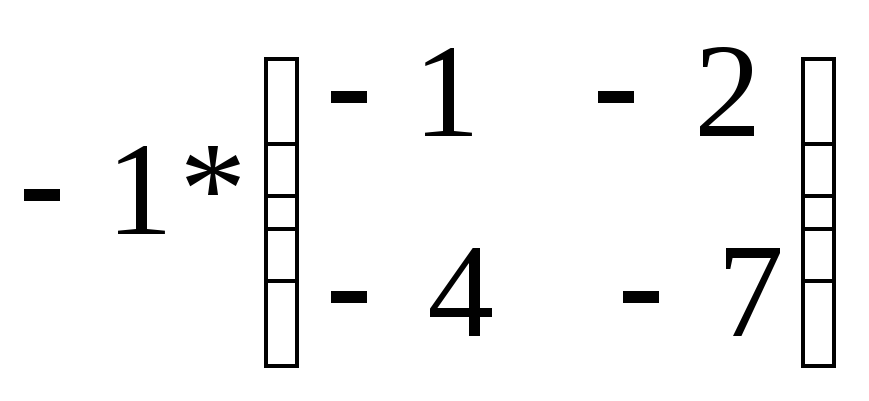
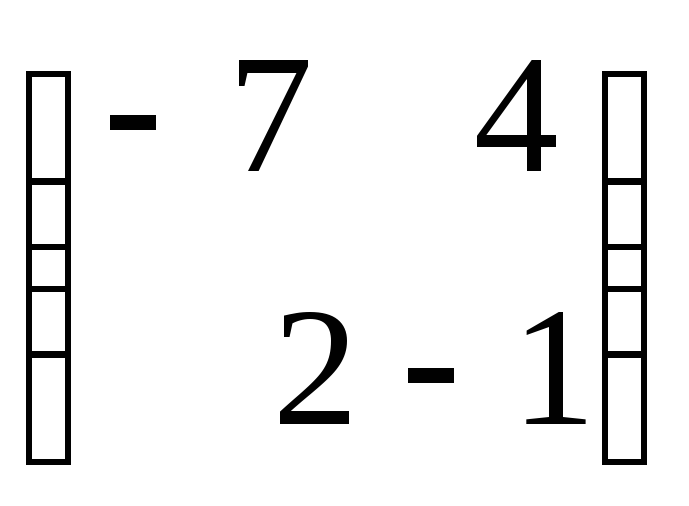
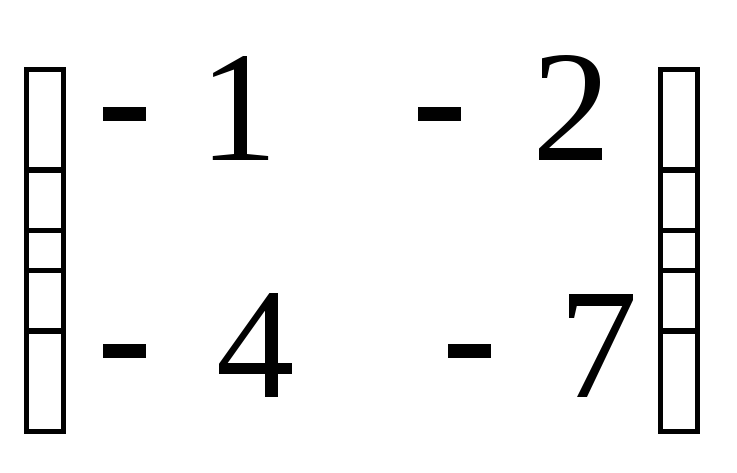
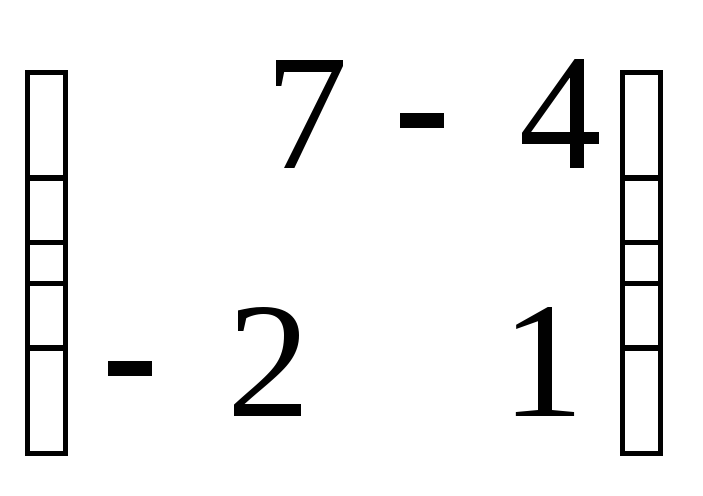
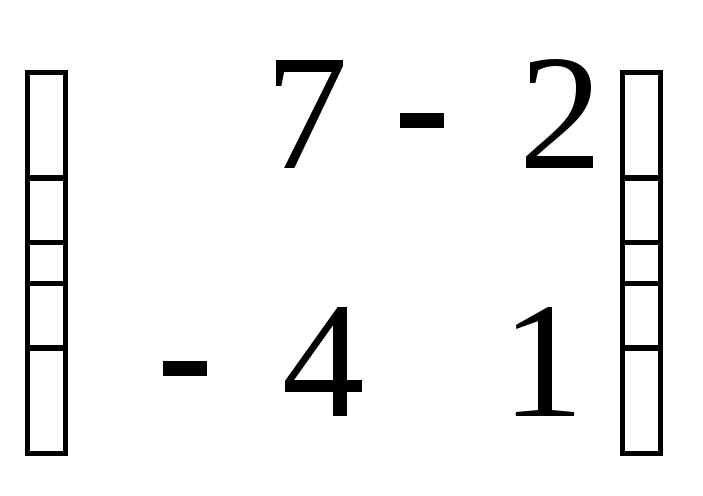
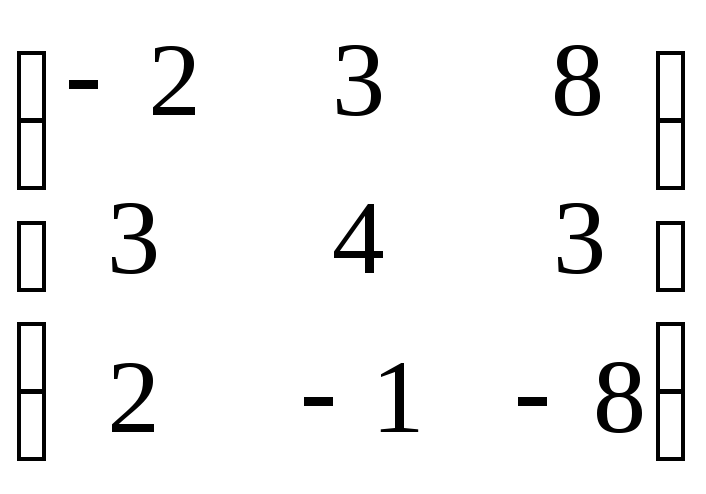
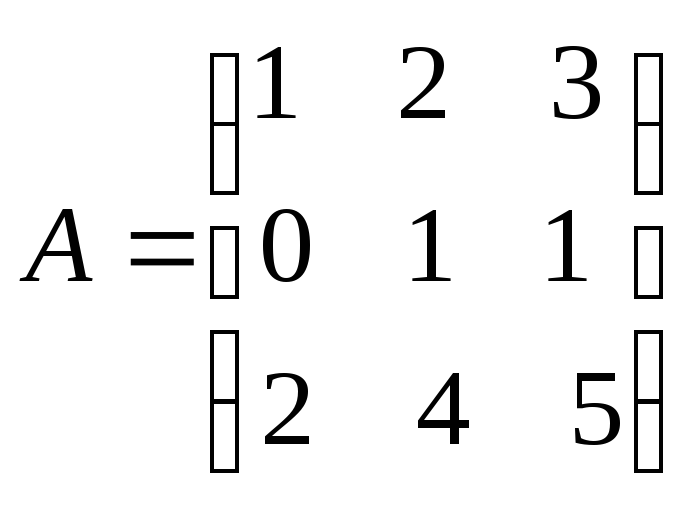
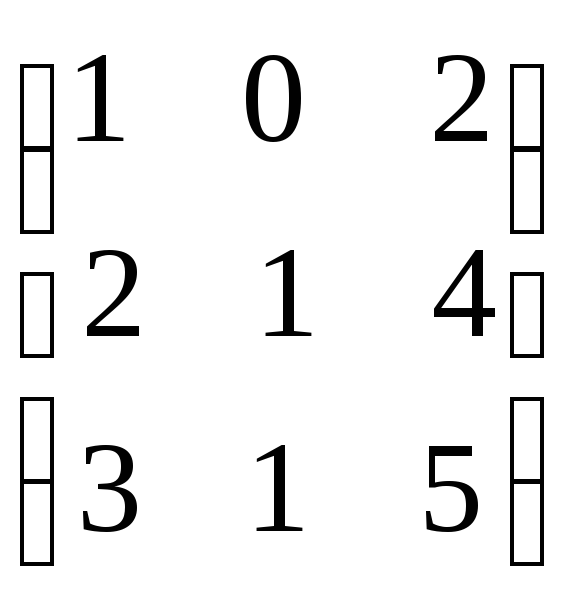
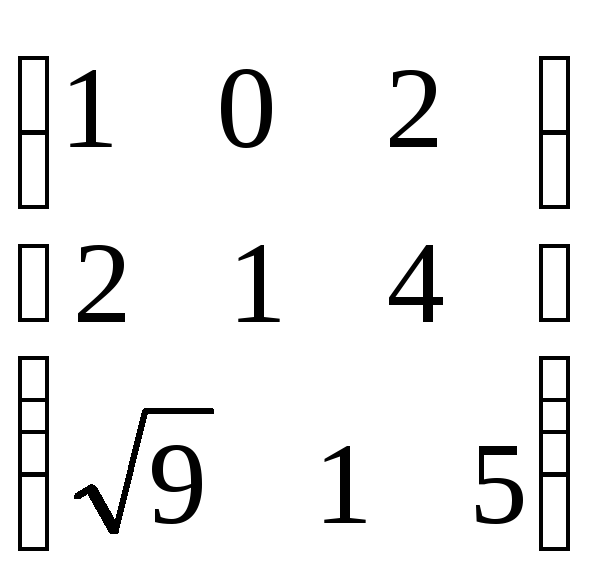
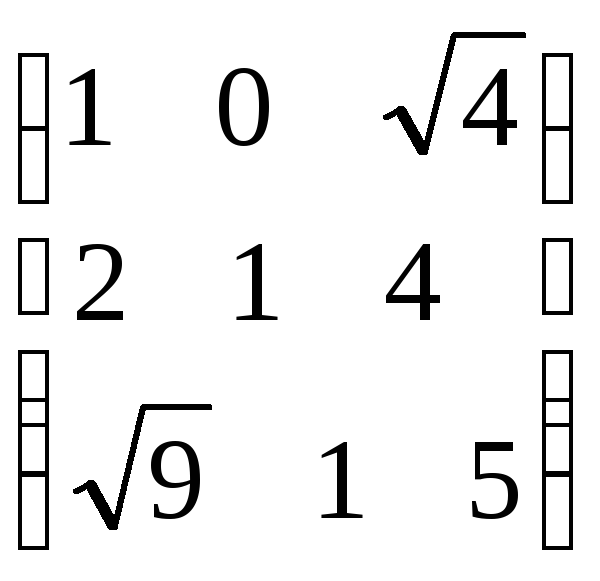
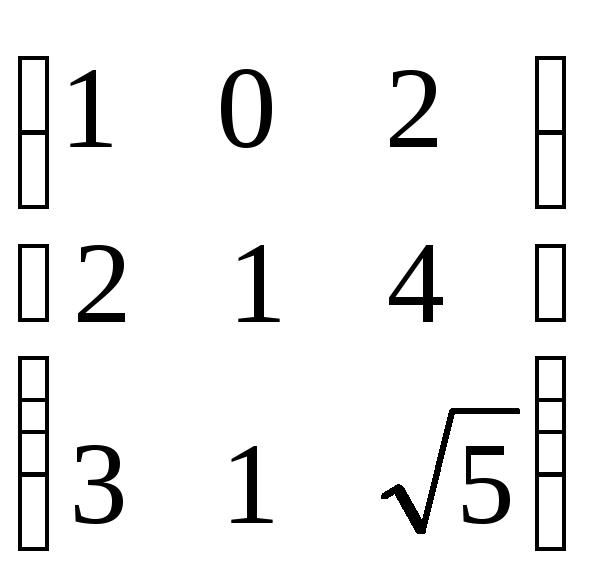
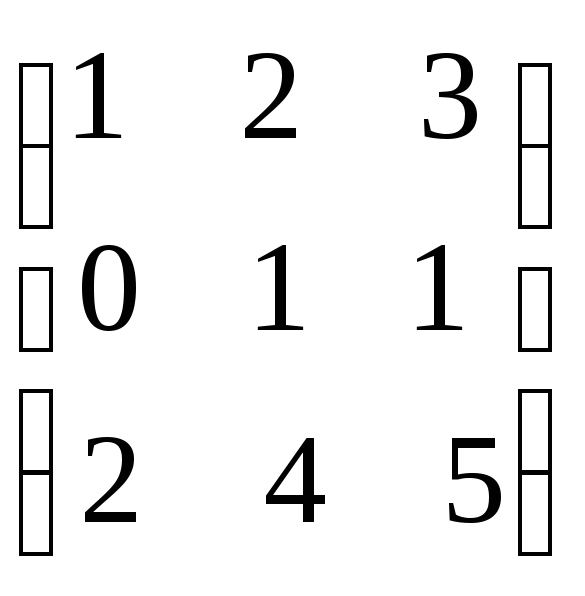
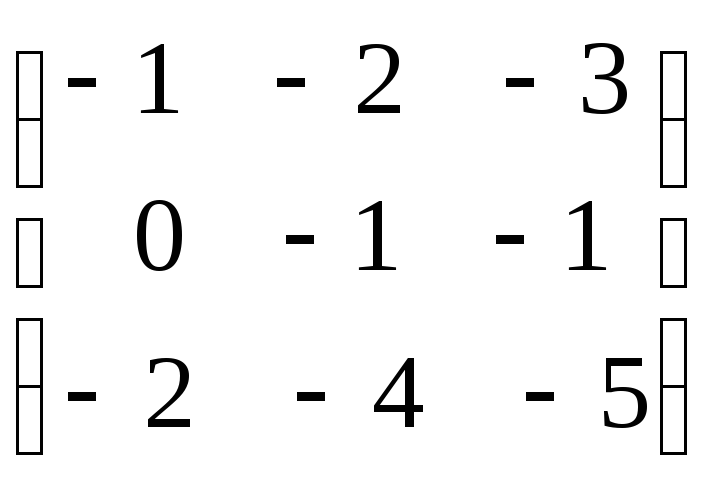
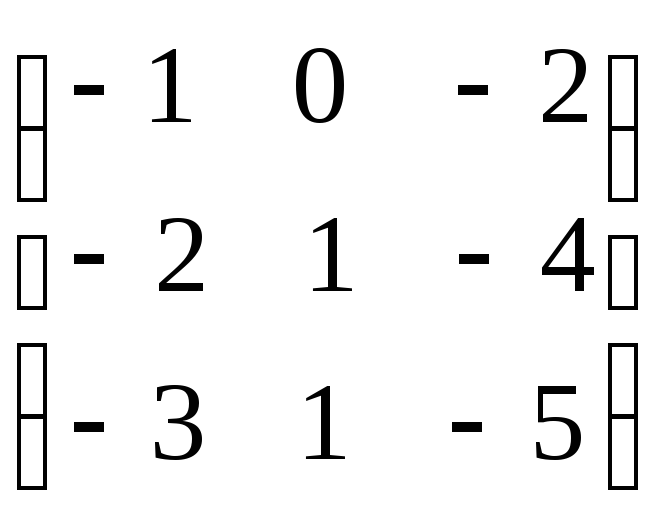
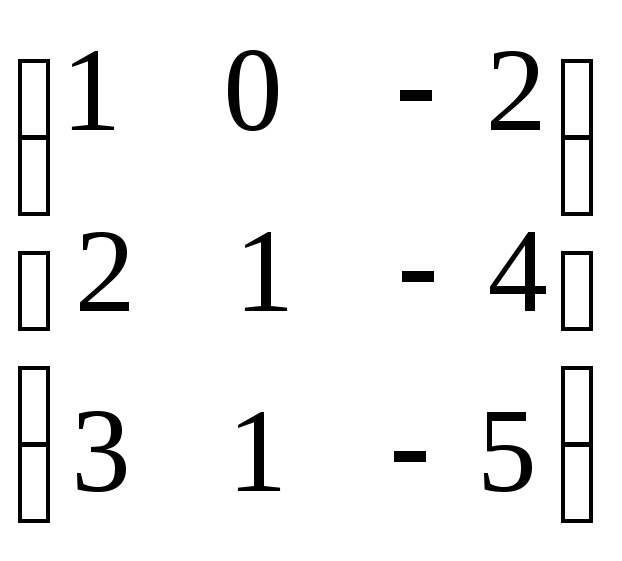
 болса, АВ
көбейтіндісін табыңыз.
болса, АВ
көбейтіндісін табыңыз.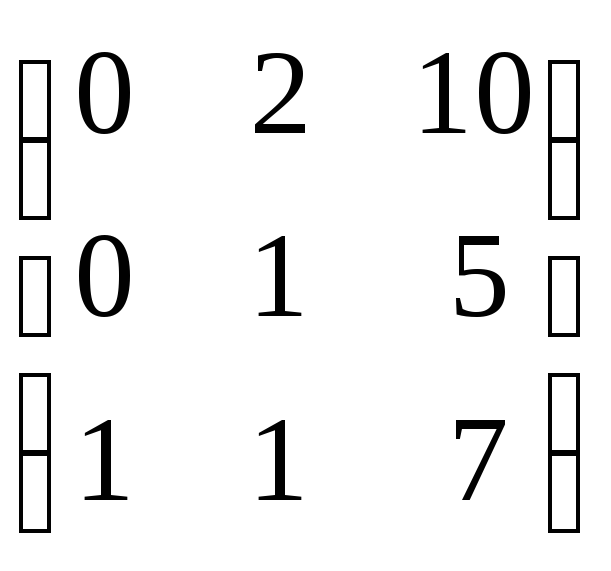
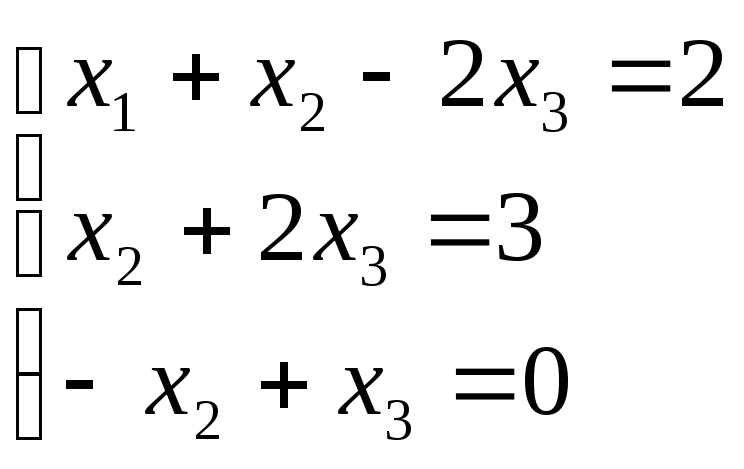
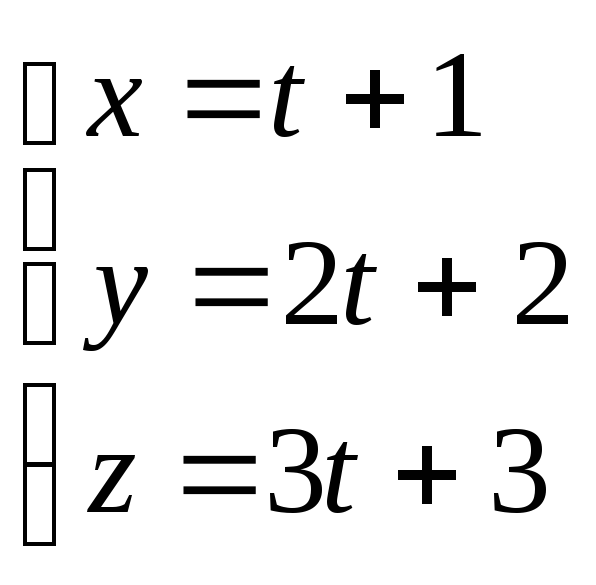
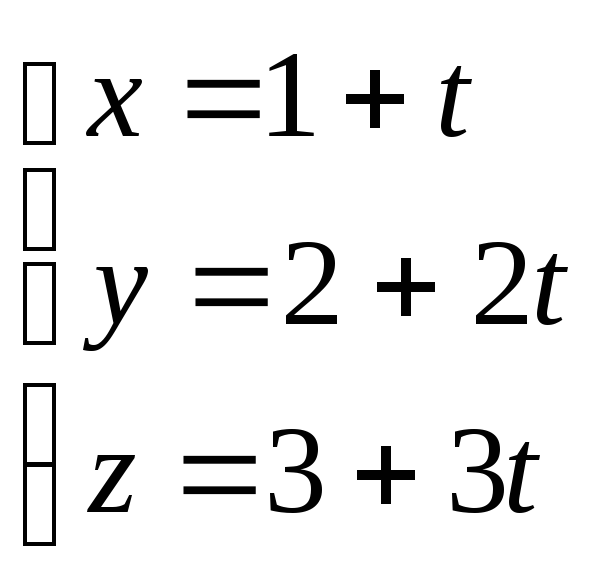
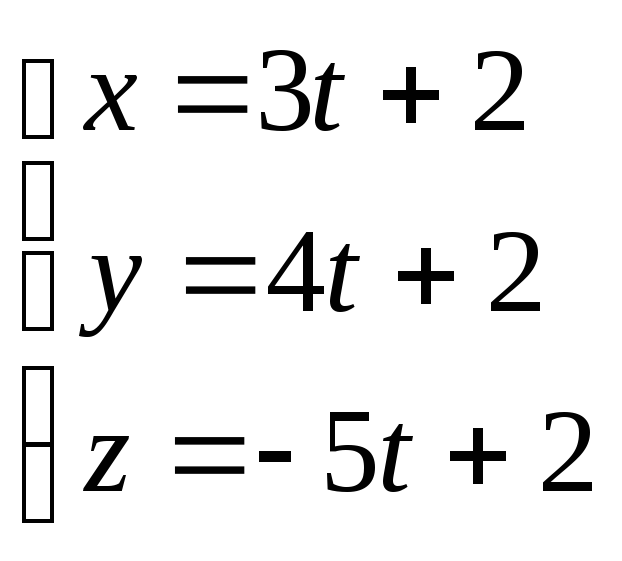
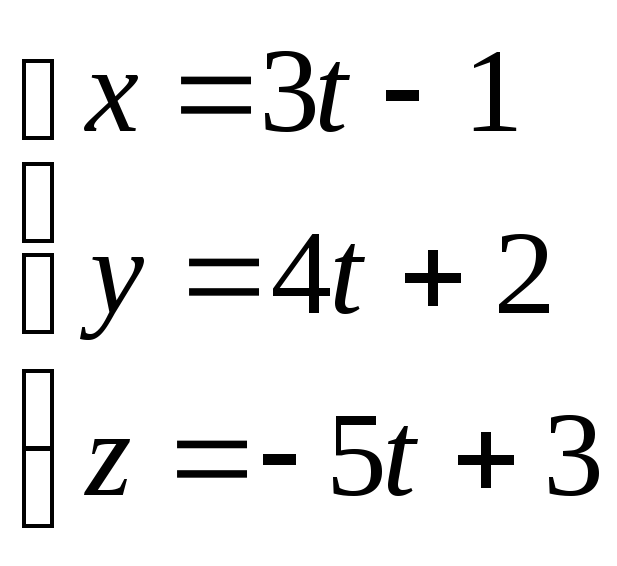
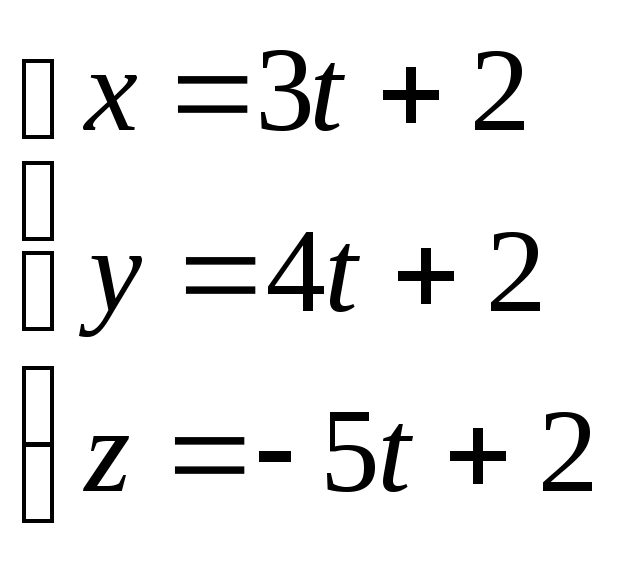

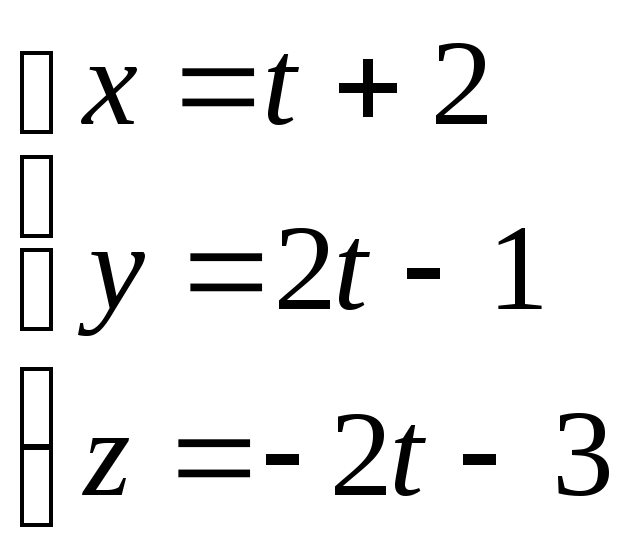
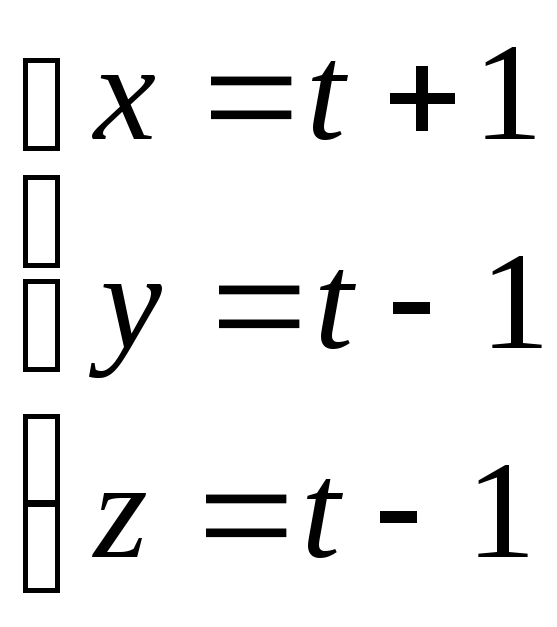

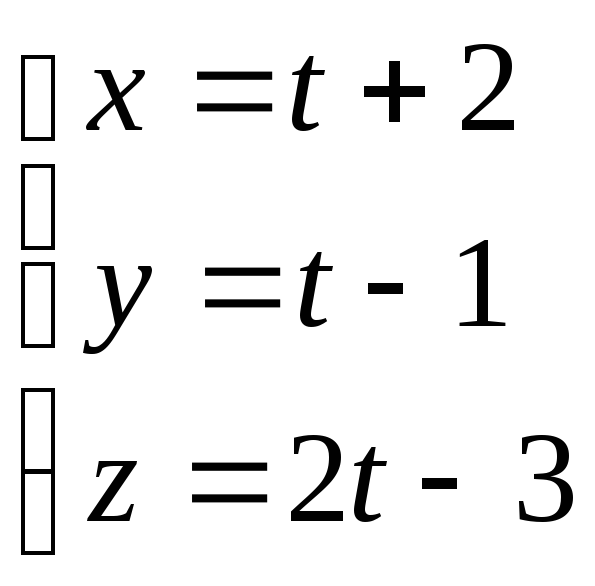
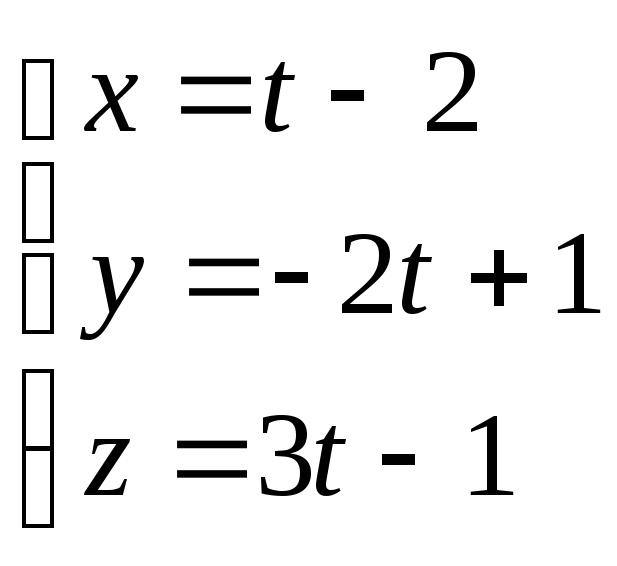
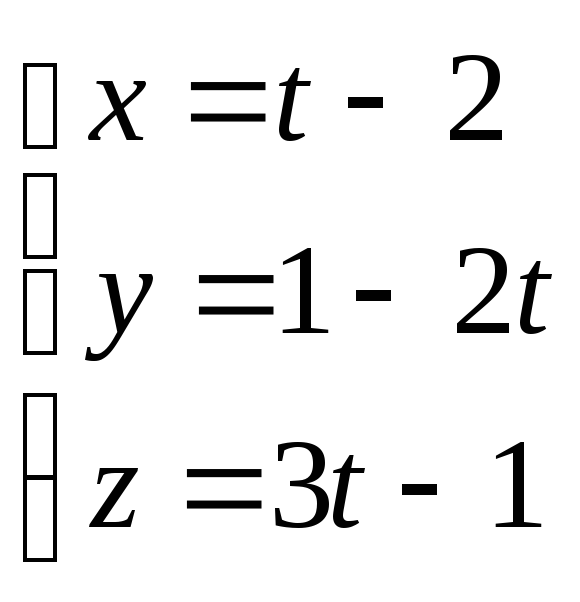
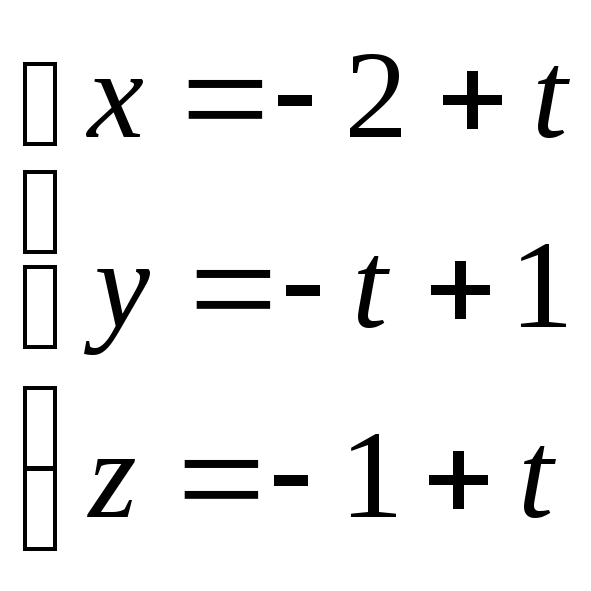
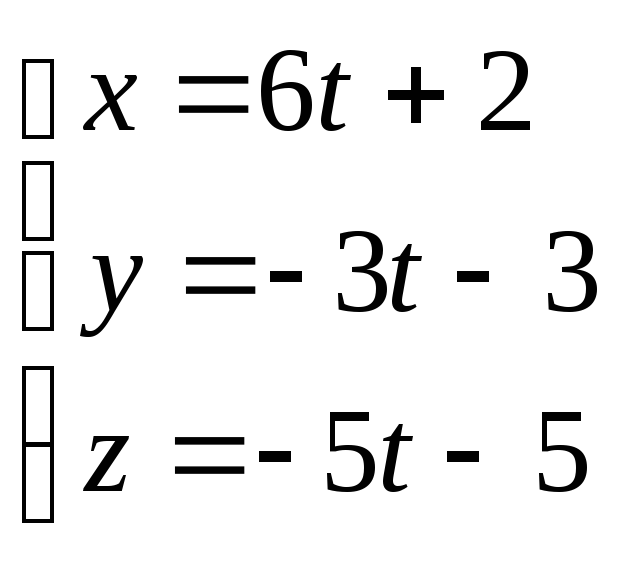
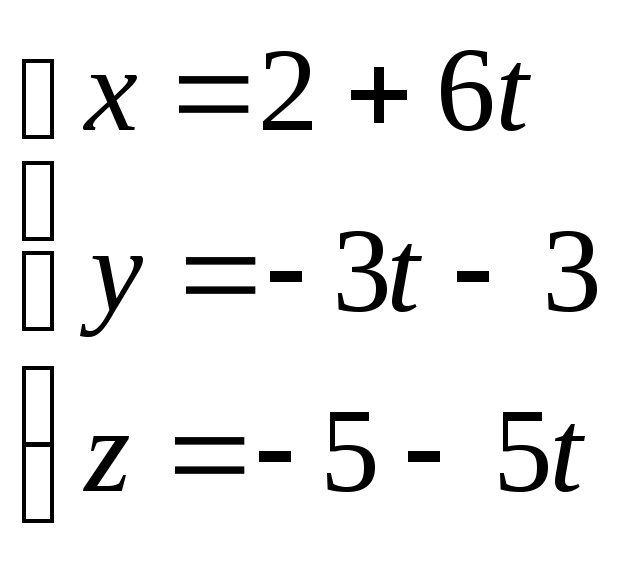
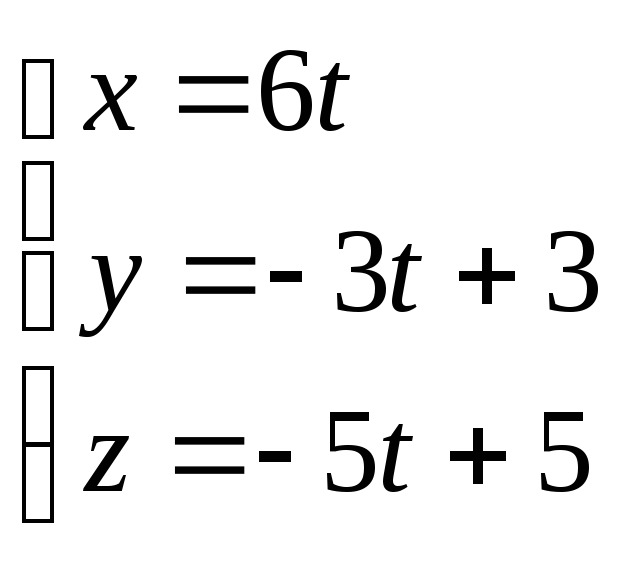
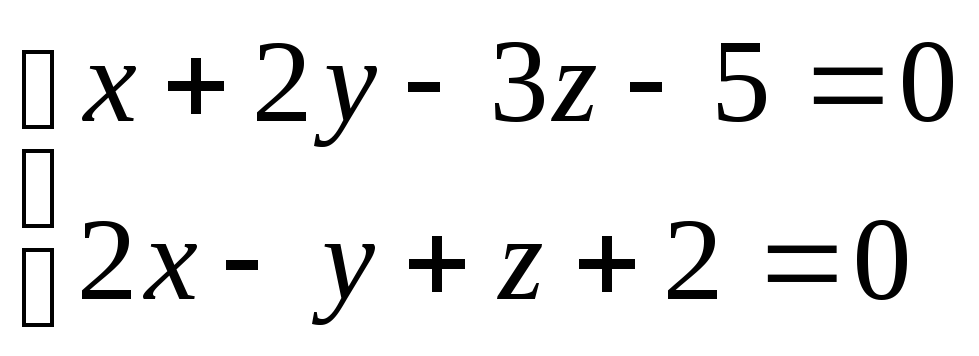 түзуінің
бағыттауыш векторын жазыңыз.
түзуінің
бағыттауыш векторын жазыңыз.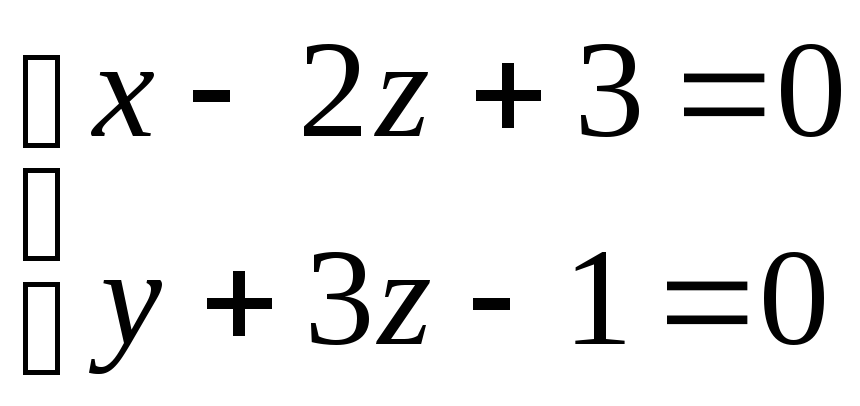 түзуі
мен
түзуі
мен
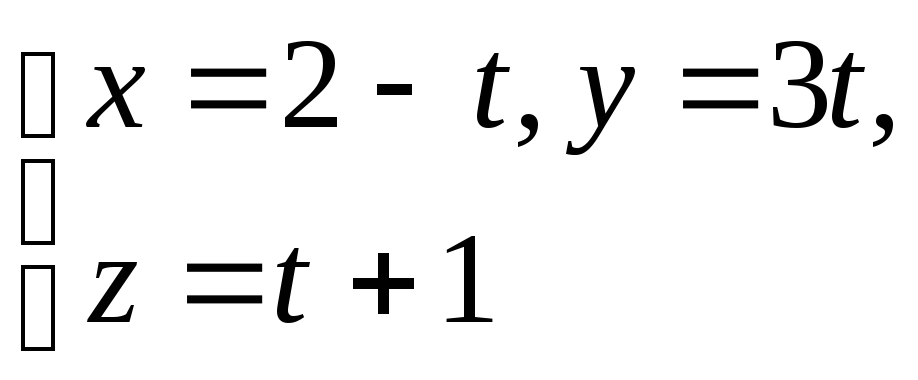 түзуі
мен
x+2y-z+3=0
жазықтығының қиылысу нүктесін
анықтаңыз.
түзуі
мен
x+2y-z+3=0
жазықтығының қиылысу нүктесін
анықтаңыз.