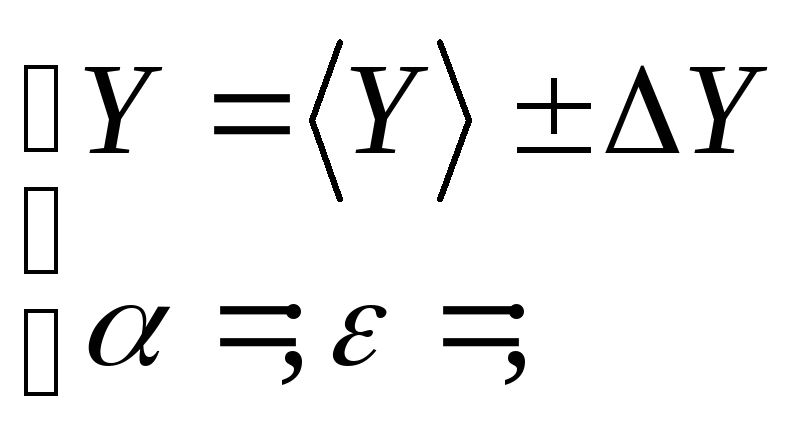§ З.Расчет погрешностей при косвенных измерениях
При косвенных измерениях для вычисления погрешности воспользуемся методом дифференциального исчисления.
Пусть искомая
величина
![]() ,
где
,
где![]() - непосредственно измеряемая
величина. Пусть при измерении величины
- непосредственно измеряемая
величина. Пусть при измерении величины
![]() допущена погрешность
допущена погрешность![]() ,
поэтому искомая величина
,
поэтому искомая величина
![]() вычисляется тоже не точно, с некоторой
погрешностью
вычисляется тоже не точно, с некоторой
погрешностью![]() .
Для того чтобы рассчитать
.
Для того чтобы рассчитать![]() ,
запишем тождество
,
запишем тождество![]() ,
затем умножим и разделим его правую
часть на
,
затем умножим и разделим его правую
часть на ![]() :
:
![]() .
.
Для малых значений
![]() справедливо соотношение:
справедливо соотношение:
![]() ,
,
следовательно,
![]() (1)
(1)
Таким образом, абсолютная погрешность функции равна абсолютной погрешности аргумента, умноженной на производную этой функции по этому аргументу.
Если искомая величина
![]() является функцией нескольких переменных
является функцией нескольких переменных
![]() ,
где
,
где![]() - непосредственно измеряемые величины
и их погрешности равны
- непосредственно измеряемые величины
и их погрешности равны![]() то при вычислении абсолютной погрешности
то при вычислении абсолютной погрешности![]() нужно учесть погрешности, вносимые
всеми этими величинами
нужно учесть погрешности, вносимые
всеми этими величинами
![]() .
Погрешность, обусловленная неточностью
измерения величины
.
Погрешность, обусловленная неточностью
измерения величины![]() будет равна, согласно формуле (1):
будет равна, согласно формуле (1):
![]()
обусловленная
неточностью измерения ![]() и т д.
и т д.
В выражении ![]() берется частная производная, потому
что в данном случае учитывается
зависимость величины
берется частная производная, потому
что в данном случае учитывается
зависимость величины
![]() только от конкретной величины
только от конкретной величины![]() ,
все остальные аргументы считаются
постоянными величинами.
,
все остальные аргументы считаются
постоянными величинами.
Рассчитав
![]() абсолютную погрешность измерения можно
вычислить по формуле:
абсолютную погрешность измерения можно
вычислить по формуле:
![]() .
.
Подставив в это
выражение значения
![]() ,
получаем:
,
получаем:
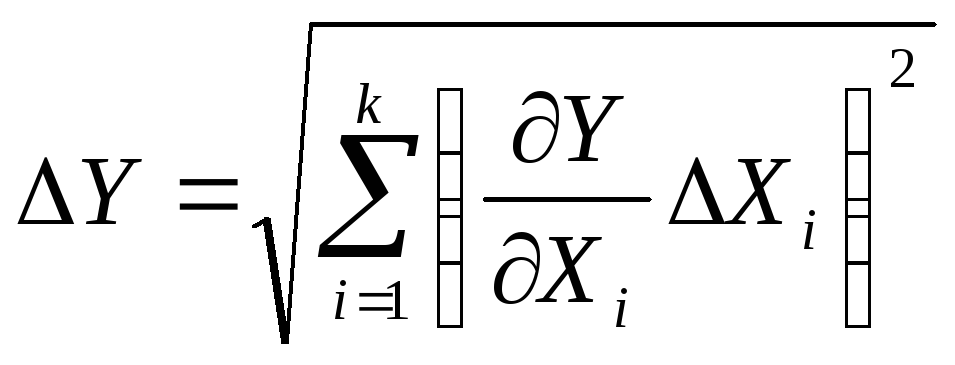 (2)
(2)
Относительная погрешность косвенных измерений вычисляется по формуле:
![]() , (3)
, (3)
где
![]() - значение функции, полученное после
подстановки в нее среднихзначений
аргументов
- значение функции, полученное после
подстановки в нее среднихзначений
аргументов
![]() .
Подставляя в (3) выражение (2),получаем:
.
Подставляя в (3) выражение (2),получаем:
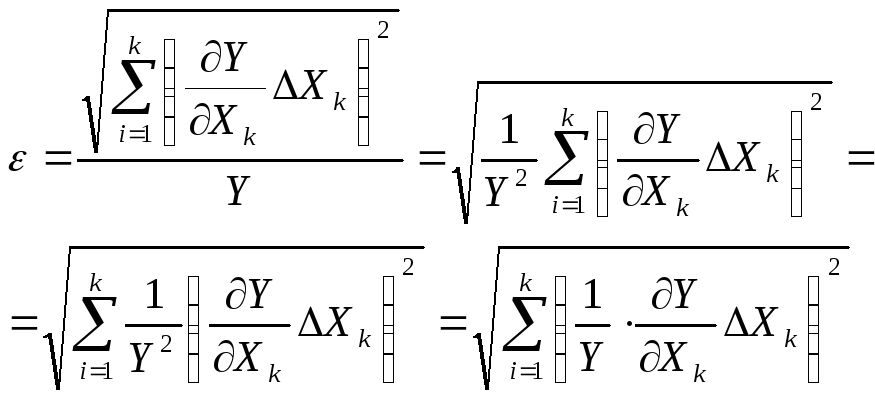
Учитывая, что
![]() получаем:
получаем:
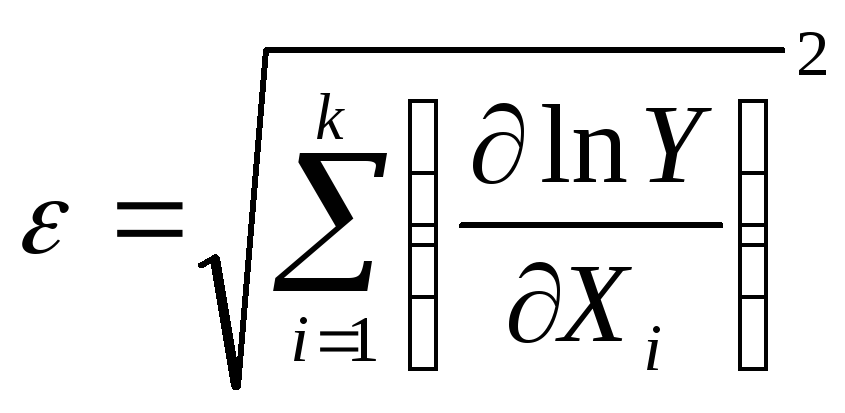 .
.
Вычисление погрешностей при косвенных измерениях.
Обработать результаты прямых измерений каждой из непосредственно измеряемых величин согласно пунктам
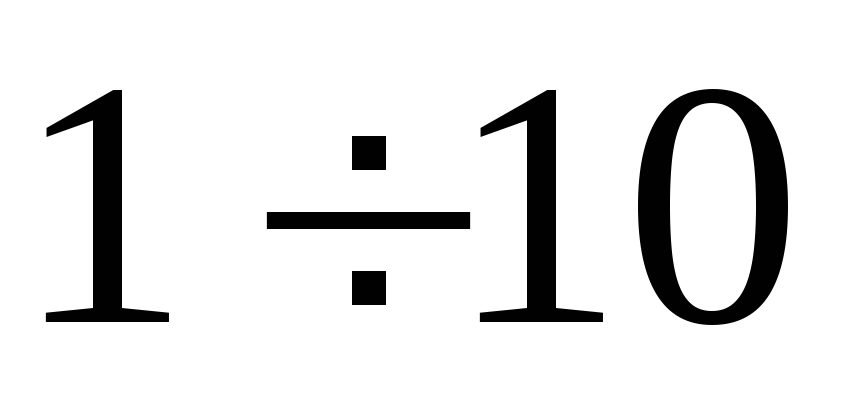 параграф 2.
параграф 2.Вычислить величину
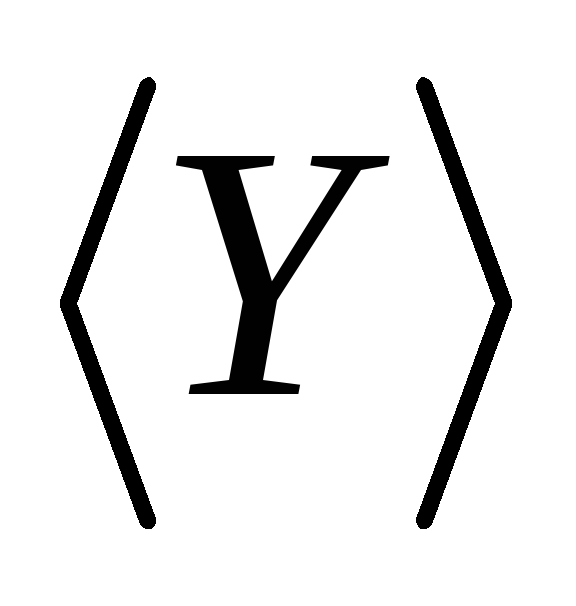 ,
подставив в расчетную формулу среднее
значение непосредственно измеряемых
величин.
,
подставив в расчетную формулу среднее
значение непосредственно измеряемых
величин.Вывести формулу для расчета
 или
или
 согласно
уравнениям (2) или
(4).
согласно
уравнениям (2) или
(4).Вычислить абсолютную и относительную погрешности результата
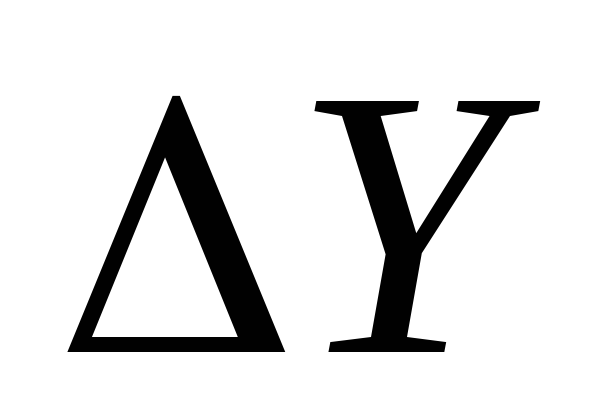 и
и .
.Провести округление результатов расчета.
Записать результат измерений в виде:

При проведении
округления пользуются теми же правилами,
что и при обработке
результатов прямых измерений. Следует
учитывать, что если
в расчетную формулу входят величины,
которые в процессе эксперимента
не измеряются и для них не указана
величина погрешности, то обычно
считается, что эта погрешность составляет
± 0,5 единицы наименьшего
разряда, представленного в числе.
Например, дана масса
![]() ,
погрешность следует принять равной ±
0,05г. Если в расчетную формулу
входят числовые постоянные (
,
погрешность следует принять равной ±
0,05г. Если в расчетную формулу
входят числовые постоянные (![]() и т.д.), то за погрешностиэтих
величин принимаются погрешности
округления.
и т.д.), то за погрешностиэтих
величин принимаются погрешности
округления.
§ 4. Вычисление погрешностей при косвенных измерениях, когда контролируемые условия не воспроизводимы
При невоспроизводимых
измерениях невозможно найти средние
значения
измеряемых величин
![]() ,
поэтому методика расчета погрешностей,
изложенная в
предыдущем параграфе, неприемлема. В
этом случае при обработке
результатов следует придерживаться
следующего порядка:
,
поэтому методика расчета погрешностей,
изложенная в
предыдущем параграфе, неприемлема. В
этом случае при обработке
результатов следует придерживаться
следующего порядка:
1 .Измерить величины
![]()
![]() раз, где
раз, где![]() - номер измеряемой величины,приписываемый
параметрам, от которых зависит
- номер измеряемой величины,приписываемый
параметрам, от которых зависит
![]() ,
,![]() -номер
измерения
величины
-номер
измерения
величины
![]() .
.
2.Рассчитать
n
раз значения
![]() ,
получив величины
,
получив величины![]() ,
где
,
где![]() .
.
3.Найти
среднее значение
![]() по формуле:
по формуле:
![]() .
.
4. Вычислить отклонение
от среднего
![]() :
:
![]() .
.
5.Определить
среднеквадратичную погрешность измерений
![]() :
:
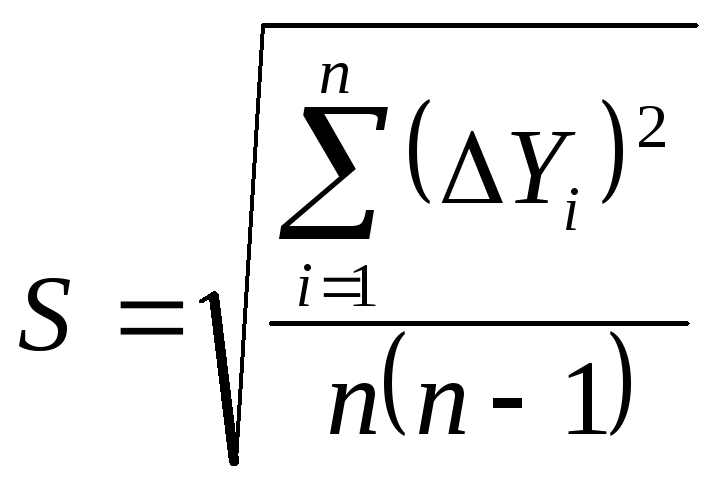
6. Задать значение
надежности
![]() и по таблице 1 найти коэффициент
Стьюдента
и по таблице 1 найти коэффициент
Стьюдента
![]() .
.
7. Рассчитать
случайную погрешность:
![]() .
.
8.Вычислить
средние значения
![]() :
:
![]()
9.Определить
приборные погрешности
![]()
10.Вывести
формулу для нахождения приборной
погрешности
![]() :
:
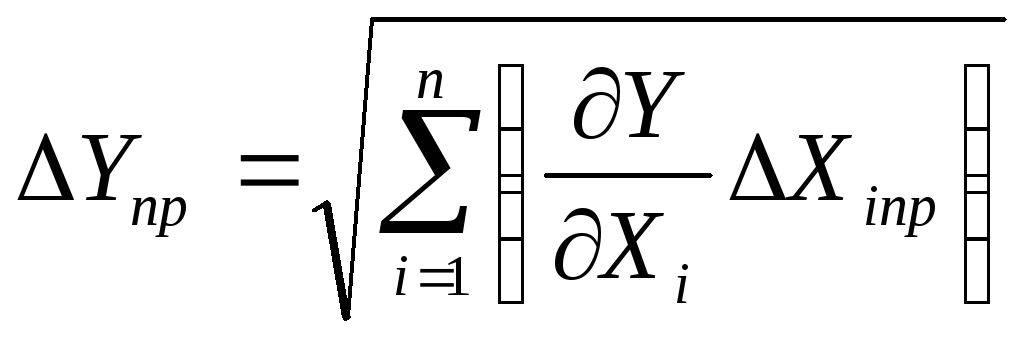
Рассчитать
 ,
подставив в полученное выражение
средниезначения
,
подставив в полученное выражение
средниезначения
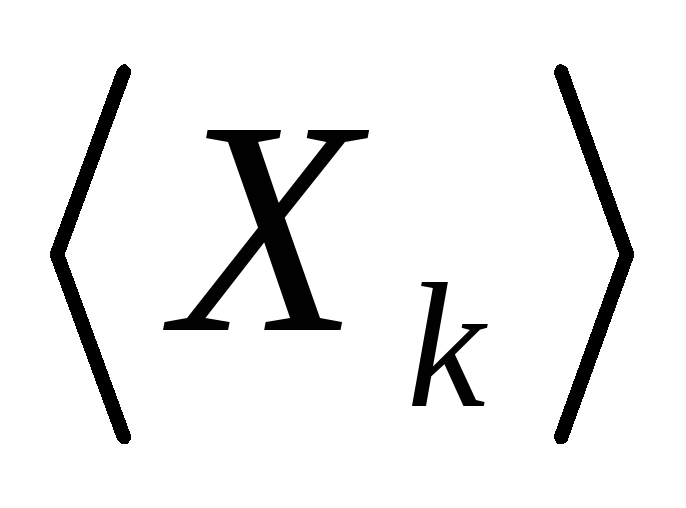 и величины приборных погрешностей
и величины приборных погрешностей
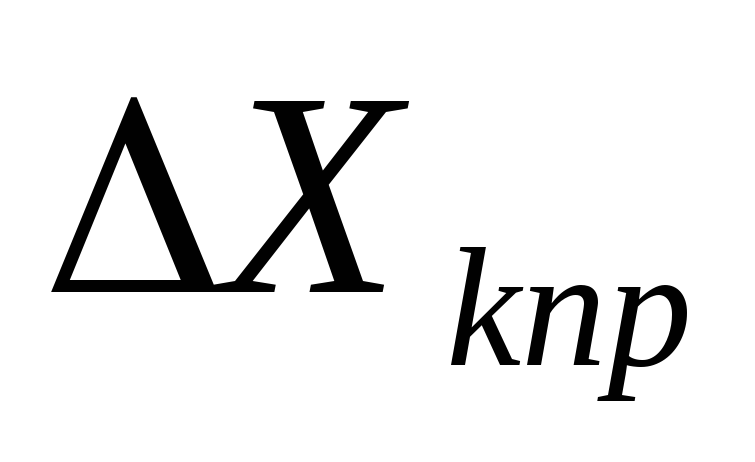 .
.Вычислить погрешность измерений:
![]() .
.
13.Найти относительную погрешность:
![]()
14.Записать полученный результат в виде: