ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОССУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«Тюменский государственный нефтегазовый университет»

ИНСТИТУТ НЕФТИ И ГАЗА

Кафедра «Автоматизации и управления»

Методические указания к практическим занятиям по дисциплине «Теория автоматического управления» для студентов специальностей «Автоматизация технологических процессов», «Электропривод и автоматика промышленных установок и технологических комплексов».

Расчёт настроек непрерывных регуляторов методом расширенных комплексных частотных характеристик

Тюмень 2005

Утверждено редакционно-издательским Советом Тюменского государственного нефтегазового университета

Составители: доцент, к.т.н. Макарова Л.Н.,

к.т.н. Макаров А.В.,

ст. преподаватель Попова Н.В.

@Государственное образовательное учреждение высшего профессионального образования

«Тюменский государственный нефтегазовый университет» 2005г.

СОДЕРЖАНИЕ

Содержание	3
1. Основные положения	4
2. Пример расчёта	8
3. Последовательность шагов при расчётах в программе MatLab	14
4. Задания для самостоятельной работы	21
5. Список литературы	23

1. Основные положения метода расчёта настроек регуляторов при ограничении на корневой показатель колебательности

1.1. Корневой показатель колебательности - величина, обратная колебательностии равная наименьшему из всех отношений действительной частикомплексных корней к мнимойхарактеристического уравнения системы.

.

1.2. При расчёте систем задаётся обычно затухание колебаний, оно должно находиться в пределахи определяется

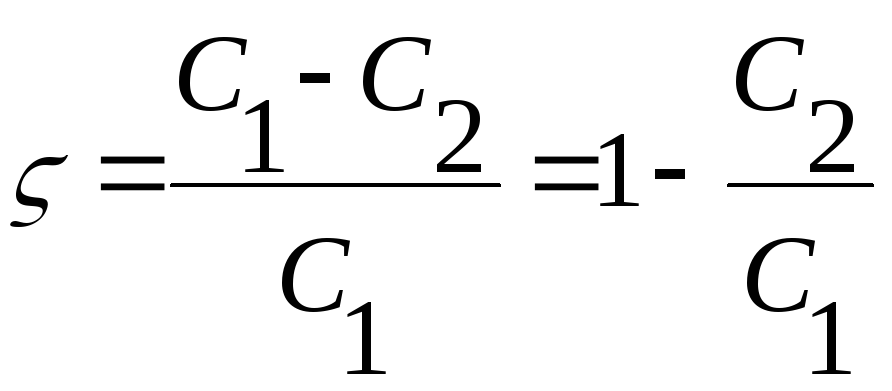, где и- амплитуды первого и второго периодов переходной характеристики соответственно.

Между колебательностью и затуханием имеется прямое соответствие:

или .

1.3. Условие, определяющее существование пары комплексно-сопряжённых корней с заданным корневым показателем колебательности для одноконтурной системы (Рисунок1) с единичной обратной связью на основе критерия Найквиста, имеет вид:

Рисунок 1. Структурная схема одноконтурной системы

где - расширенная амплитудно-фазовая частотная характеристика (АФЧХ) регулятора,

- расширенная АФЧХ объекта.

1.4. Для ПИ-регулятора с передаточной функцией расширенная АФЧХ имеет вид

1.5. Для ПИД – регулятора с передаточной функцией расширенная АФЧХ имеет вид

где ,

Т_д – постоянная дифференцирования,

Т_и – постоянная интегрирования,

,

- балластная постоянная.

1.6. Из условия существования пары комплексно-сопряжённых корней и на основании свойства комплексных чисел

вытекает равенство

Тогда для ПИ-регулятора:

(1)

Разрешив систему (1) относительно и, получим

(2)

1.7. Расчёт проводится внутри диапазона частот ;

находят из условия:

,что соответствует; (3)

из условия:

,что соответствует. (4)

Чтобы найти и , проводят и сводят в таблицу следующие расчёты (Таблица 1) для произвольно заданных частот, добиваясь выполнения равенств (3) и (4).

Таблица 1. Расчёты для определения и

1.8. Разбивают интервал нашагов; для каждой частотырассчитывают по (2) значенияии сводят в таблицу (Таблица 2).

Таблица 2. Значения настроек для разных значений частот

Настройки считаются оптимальными, если отношение максимальное. Полученные настройки должны обеспечить прямые и косвенные показатели качества, поэтому показатели качества рассчитывают при найденных параметрах регуляторов().

1.9. Для определения прямых показателей качества нужно построить переходную характеристику замкнутой системы, поэтому записывается передаточная функция замкнутой системы ():

Находится изображение переходной характеристики ():

и, используя обратное преобразование Лапласа, строится переходная характеристика системы ():

.

1.10. По переходной характеристике вычисляются прямые показатели качества: перерегулирование ; время регулированияи т.д.

1.11. По амплитудно-частотной характеристике замкнутой системы определяются косвенные показатели качества.

2. Пример расчёта

Задание. Рассчитать настройки ПИ – регулятора методом расширенных комплексных частотных характеристик (АФЧХ) системы на основе заданного корневого показателя качества (), структурная схема приведена выше (Рисунок 1), передаточная функция объекта имеет вид:

.

Решение

2.1. Расширенная АФЧХ (или КЧХ) ПИ - регулятора

.

2.2. Условие, определяющее существование комплексно-сопряжённых корней:

2.3. Составляем основную систему для расчётов

или

т. е.

2.4. Тогда расчётные формулы для настроек (и) имеют вид:

2.5. Выделяем диапазон изменения частот, обеспечивающих оптимальные настройки. Для этого, изменяя частоту от с шагом 0,0001, строим таблицу (Таблица 3) до тех пор, покастанет несущественной величиной.

Замечание. В таблице приведены не все значения в целях экономии места.

Замечание. В интервале частот, где приближается к, для получения большей точности нужно уменьшить шаг. Для ускорения убыванияпосле прохожденияшаг нужно увеличить.

Таблица 3. Значения действительной и мнимой частей обратной расширенной комплексной частотной характеристики объекта

0,001	0,083106	0,00066599	0,00022644
0,0011	0,083083	0,00073251	0,00024905
…	…	…	…
0,1509	0,028991	0,085116	0,028939
0,151	0,028941	0,085162	0,028955
0,1511	0,028892	0,085208	0,028971
…	…	…	…
0,9802	-0,98857	0,0001281	0,0000435
0,9803	-0,98877	0,0000614	0,0000209
0,9804	-0,98896	-0,0000052	-0,0000018

;

2.6. Интервал [;] разбиваем на 15 подинтервалов :

... Для каждой частоты рассчитываем и.

Замечание. Можно считать сначала

, а после определения наибольшего отношения высчитать значенияи.

Замечание: После определения приблизительного значения нужно уточнить это значение, построить интервал в окрестностис более мелким шагом. Результаты расчётов сведены в таблицу 4.

Таблица 4. Зависимость отношения от частоты

0,151	0,014346
0,23393	0,030988
0,31686	0,050538
0,39979	0,070398
0,48272	0,087973
0,56565	0,10067
0,64858	0,10589
0,73151	0,10103
0,81444	0,083506
0,89737	0,050717
0,9803	6,7184e-005
0,151	0,014346
0,23393	0,030988
0,31686	0,050538
0,39979	0,070398
0,48272	0,087973

итак, ,,.

2.7. Построение переходной характеристики

При нарушении равновесия системы автоматического управления в ней возникают переходные процессы. Реакция на единичное ступенчатое воздействие () или ступеньку, называется переходной характеристикой () :

,

где - передаточная функция замкнутой системы; в примере для приведённой структурной схемы:

,

,

Перерегулирование

, .

2.8. Для уменьшения можно попытаться уменьшить, например, оставивтем же. Тогда;

время регулирования при ;12c;

степень затухания .

Для расчёта настроек ПИД регулятора данный метод оказывается слишком громоздким и сложным.