5. Профильные разрезы

Рассмотрим построение разреза по данным ГИС, т.е. с использованием каротажных диаграмм. Основная идея – построение разреза производится теми же программными средствами, что и картопостроение.

Если струк. карту можно рассматривать как изображение функции глубины залегания поверхности от двух переменных (х;у),то границы на профильном разрезе можно рассматривать тоже, как изолинии значения некоторой финкции, которая задается тоже двумя переменными (координата Х и глубина).

Для получения сопоставимых с другими методиками результатов важно правильно выбрать функцию, которая будет использоваться для построения разреза таким способом.

Если нам нужен литологический разрез, то роль такой функции с приемлемыми результатами может сыграть кривая сопротивления 2х-метрового зонда (GZ3), т.к. проводилась серия экспериментов по применения геофизических методов и их комбинаций, и, согласно, критерия Стьюдента (применяемого при исследованиях) этот зонд давал наибольшую информативность. Тогда последовательность построения профильного разреза сводится к следующему:

1 выбирается направление профиля, а соответственно скважины, вдоль которых он будет проходить

2. выбирается интервал глубин, в котором необходимо построить профильный разрез (единый для всех скважин)

3. кривая GZ3 для каждой из скважин аппроксимируется сплайном, при этом шаг должен быть одинаковым для всех скважин.

4. Нужно отбросить бракованные значения (например, -999)

5. Определяется расстояние между скважинами по профилю, т.е. определяется координата Х для каждой скважины

6. Собирается таблица данных для построения профиля

Например: X h GZ3

1.24 800 ...

1.24 804 ...

1.24 808 ...

3.56 800 ...

3.56 804 ...

И т.д

7. данные подаются на вход в программу

При необходимости учета сейсмики ее дополняют в качестве априорной информации на этапе картопостроения.

1.6 ТРЕХМЕРНЫЕ МОДЕЛИ

3х-мерная модель характеризует изменение свойств в пространстве, структурой которого является сетка, а ее ячейки содержат значение какого-либо параметра.

Модели бывают:

• статические (3Д-геология) - на начало разработки

• динамические (гидродинамика)

3х-мерная сетка – это ячеистый каркас, внутри которого происходят все основные этапы геологического моделирования. Главное отличие 3х-мерной сетки от 2х-мерного грида заключается в том, что ячейка 3х-мерной сетки занимает определенный объем в пространстве и имеет три координаты (x, y,z), ячейки 2х-мерного грида характеризуются только площадью.

Значение параметра заключается в центральной точке ячейки 3х-мерной сетки.

Горизонтальное разрешение сетки определяет размерность dX и dY. При выборе горизонтального разрешения шага нужно учитывать:

1. расстояние между скважинами (необходимо, чтобы между скв. было минимум 2-3 ячейки)

2. размер моделируемого участка

3. аппаратные возможности ПК

чаще используют сетки 50х50, 100х100, реже 200х200.

Вертикальное разрешение сетки – размерность dZ.

Исходные данные для 3Д моделирования:

1. Координаты устьев скважин

2. Инклинометрия

3. Координаты пластопересечений

4. Стратиграфические разбивки

5. Кривые ГИС в формате *las

6. РИГИС (интерпретация ГИС)

7. Отбивки флюидных контактов

8. Сейсмические данные

9. Уравнения петрофизических зависимостей например, LgКпр=f(Кп)) и «керн-ГИС» (например, Кп=f(αпс)

2.1 СЕЙСМОРАЗВЕДОЧНАЯ ИНФОРМАЦИЯ

Если строится карта горизонта с привлечением сейсмики, то следует сейсмические данные пересчитать в углы падения, т.е производные.

Если метод картопостроения позволяет настраивать анизотропность, то необходимо учитывать направление сейсмических профилей.

С применением карт углов падения можно очень четко увидеть разломы.

2. РАСПОЗНАВАНИЕ ОБРАЗОВ

Образ рассматривается как класс объектов, а класс может быть применен к большому количеству.

Пусть есть множество точек.

красная прямая делит два класса с минимальным количеством ошибок (нужно найти ее).

Х ϵ(принадлежит) R1-плотность вероятности 1 класса

Х ϵ R2-плотность вероятности 2 класса

R – это выборки.

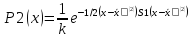
S-матрица ковариации

S1= S2

Находим отношение 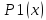к

И остается:

3.5 МОДЕЛИ ЗАЛЕЖЕЙ

В рассматриваемых ниже примерах моделируются профильные разрезы залежей. Они носят иллюстративный характер и непосредственно в оценке запасов не участвуют. На интервале [9 10] заданы две функции f (парабола) и g (горизонтальная прямая). Их совместный график приведен на рисунке 63.

Рис. 63. Совместный график функций f и g.

Процедура min(f,g) оставляет на графике одну из двух функций, ту, значение которой меньше (рис. 64).

Рис. 64. Комбинированная кривая min(f,g)

Если функций 3, а не 2, то соответствующая процедура записывается в виде min(f,min(g,h)). Сначала находится минимальная из функций g и h, затем полученный результат сравнивается с f. Точно так же работают операции поиска максимальных значений, объединения и пересечения множеств (функции должны быть заданы численно). На этой основе ниже получены выражения, которые иллюстрируются рисунками.

Пример. Пластовая сводовая залежь.

В приведенном ниже примере hk- кровля пласта; hp – его подошва; g – ВНК. Исходные кривые и окончательный результат приведены на рисунке 65. Вверху ВНК в виде непрерывной линии, внизу он проведен только внутри пласта. Выражение, которое позволяет этого добиться (формула залежи), hh=[min(hk,max(g,hp));hk;hp]. В формуле операция объединения заменена на точку с запятой.

Рис. 65. Модель пластовой сводовой залежи

Если добавить поверхность несогласия gg=ones(1,51)*7, то можно получить модель, изображенную на рисунке 66.

Рис. 66. Модель пластовой сводовой залежи, осложненной

поверхностью несогласия

Формула залежи, осложненной поверхностью несогласия, hh=[min(hk,gg);min(hk,max(hp,g));hp]. Если в квадратных скобках через точку с запятой добавить gg, то поверхность несогласия распространится на весь рисунок.

На следующем рисунке (67) gg – ГНК. Поэтому кровля пласта не удалена

Рис.67. Модель пластовой сводовой залежи с газовой шапкой

hh=[min(hk,gg);min(hk,max(hp,g));hp;hk] Добавили только кровлю и получили модель залежи с газовой шапкой. gg теперь – ГНК

Модель залежи в базальном песчанике приведена на рисунке 68.

Рис. 68. Модель залежи в базальном песчанике, прилегающем к выступу фундамента. Поверхность фундамента обозначена hf. Формула залежи hh=[min(max(hk,hf),max(g,hf));max(hk,hf);hf]

Приведенные примеры ясно показывают, что любую залежь можно описать простым математическим выражением.

4.2 ОШИБКИ КАРТ

1) σ² = σ² *β^т* (А^т*А)^-1*β – если задача решается, МНК без стабилизаторов

β – вектор базисных сплайнов(функций),в той точке, которой мы вычисляем ошибку.

А^т*А – матрица системы уравнений (S)

β^т * S^-1* β – в простом МНК

Вычисляем во всех узлах эти ошибки и получаем карту.

Когда вариационная задача:

S = А^т*А+αQ – матрица системы

Эта задача решается с помощью amnkd.

2) Считали (f) при разных ρ (вес на точки), складывали их и получали:

f = (f₁+f₂+…+f_n) / n;

находим дисперсию: S² = ((f₁-f).*(f₁-f)+(f₂-f).*(f₂-f)+…+(f_n-f).*( f_n-f)) / (n-1)

Они перемножаются покомпонентно, и получается, что дисперсия вычисляется в каждом узле.

3) Находим карту при стабилизаторе D₂ и D₁. При D₁ в точках min погрешность, а между точками стремится к 0.

4.3 ЭНТРОПИЯ

ЭНТРОПИЯ – мера неопределенности некоторых ситуаций.

P(xi) – вероятность i-го уравнения х.

Энтропия не зависит от типа распределения. Х можно представить как некоторую величину, меняющуюся во времени и пространстве.

Пусть есть событие, что Z1>2.5 и что Z2<=2.5 у них есть свои вероятности

Р(х1)=3/5 и Р(х2)=2/5 следовательно энтропия величины Z равна:

Н(х)=-(3/5*log(3/5)+2/5*log(2/5)= - (3/5(-0.22)+2/5(-0.4))= 0.292

Возможный диапазон изменчивости энтропии [0;log(n)] , где n-возможное количество значений. Нижняя граница, равная нулю, означает отсутствие неопределенности, т.е. х=const. Графически это можно выразить так:

Верхняя граница, равная log(n) – все значения встречаются с равной вероятностью. Энтропия безразмерная величина, поэтому есть возможность сравнивать степень изученности разных величин, а следовательно можно сравнивать энтропии разных моделей. Например, при подсчете запасов сделать вывод о том, какое месторождение более изучено, а какое менее. Энтропия имеет аналог – дисперсия.