4. Алгебра на множестве карт.

Логические операции со значениями поля в точках (или с коэффициентами сплайн) дают возможность получить индикаторные или характеристические функции, принимающие значения 1 (истина) или 0 (ложь).

Выражение 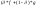позволяет получить карту f там, где δ>0 и карту g там, где δ=0. Поскольку операции совершаются на множестве точек знак «+» можно заменить символом объединения множесв . Использование логических операций и алгебры множеств позволяет строить сложные поверхности, составленные из фрагментов различных поверхностей.

5. Структура множества моделей

f, если f<g

min(f,g) = g, если f>g

max(f,g)g

[max(g,f);g]

min(f,g)g

[min(h,g);max(f,g);g]

С помощью алгебраических операций можно анализировать структуру множества поверхностей. К сожалению наглядно ее можно иллюстрировать только на профильных разрезах.

f_i=λ_if₁ линейная зависимость геологических границ;

max(f,g)Ug – g несогласно залегает на f;

min(f,g)Ug – f несогласно залегает на размытой поверхности g;

min(h,g)Umax(f,g)Ug – g граница перерыва, h граница в подперерывном комплексе, f граница в надперерывном комплексе.

6. Преобразование структурных карт в геологическую и обратно.

Пусть {f} – множество геологических границ (карт); g – карта рельефа. Выражение (f_i>g)∩(f_i-1<g)*n_i выделяет полосу выходов толщи, расположенной между границами f_i и f_i-1; n_i – число, цвет, штриховка, отличающие толщу от других толщ. Для самой молодой и для самой древней толщи остается только одно из неравенств. Таким способом емейство структурных карт преобразуется в геологичекую карту или карту среза, если g – плоскость.

Переход от геологической карты к структурной требует определить отметки выбранной границы по ее выходам на поверхности рельефа. Другой источник информации – простирание пород. Выходы любой границы прослеживаются на одном элементе рельефа (холм , структурный нос, лощина) две ближайшие точки пересечения геологической границы с одной изолинией карты рельефа надо соединить прямой линией. Простирание линии совпадает с простиранием пород. Для такого подхода можноиспользовать не обязательно границы стратиграфических подразделений. Вполне приемлемо прослеживать какую-нибудь грвку, смену растительности и тому подобное. Ввод в программу отметок и простирания (градиент по направлению простирания равен нулю) достаточен для получения удовлетворительной структурной карты.

7. Тектонические схемы.

Тектонические схемы чехла строятся путем выделения замкнутых поднятий разного порядка. Более сложная проблема выделение седловин. Для этого необходимо прежде всего найти седловые точки, из каждой из них провести провести лучи по всем направлениям до пересечения с замыкающей изолинией смежных поднятийв точках пересечения вычислить градиент поля. В точках касания скалярное произведение векктора,совпадающего с лучом и градиента равно нулю (векторы ортогональны). Так как угол между векторами конечен, то склярное приозведение будет отлично от нуля. Надо просто выбрать точку по минимуму. В окрестности седловой точки будет найдено 4 таких точки. Их необходимо попарно соединить кривыми, параллельными внешним изолиниям.

Берется карта по отражающему горизонту Б и строится одна сводная карта. Если мы проведе некоторые изолинии, то на этой карте выделятся крупные складки, своды, сиеклизы.

f – градиент f

m – направление m

(mi, f) – это будет точка касания луча, кот. выходит из седловой точки.