Глава 3. Плоские электромагнитные волны и их свойства

1. Общие свойства волновых процессов

Прежде чем рассматривать волновой процесс, дадим определение колебательного движения. Колебание – это периодически повторяющийся процесс. Примеры колебательных движений весьма разнообразны: смена сезонов года, колебание сердца, дыхание, заряд на обкладках конденсатора и другие.

Уравнение колебанияA(t) в общем виде записывают в виде

, (3.1)

где - амплитуда колебаний,- циклическая частота,- время,- начальная фаза. Часто начальную фазу принимают равной нулю.

От колебательного движения перейдем к рассмотрению волнового движения.Волна – это процесс распространения колебаний в пространстве с течением времени. Так как колебания распространяются в пространстве с течением времени, то в уравнении волны необходимо также учесть пространственные координаты и время. Уравнение волны A(z,t) имеет вид

, (3.2)

где А₀ – амплитуда, w - частота, t – время, b - волновое число, z – координата.

Физическая природа волн весьма многообразна. Известны звуковые, электромагнитные, гравитационные, акустические волны.

По типу колебаний все волны классифицируют на продольные и поперечные. Продольные волны – это волны, у которых частицы среды колеблются вдоль направления распространения волны (рис. 3.1а). Примером продольной волны является звуковая волна.

а б

Рис. 3.1 Продольные и поперечные волны

Поперечные волны – это волны, у которых частицы среды колеблются в поперечном направлении относительно направления распространения (рис. 3.1б).

Электромагнитные волны относятся к поперечным волнам. Следует учесть, что в электромагнитных волнах происходит колебание поля, и никакого колебания частиц среды не происходит. Если в пространстве происходит распространение волны с одной частотой w, то такая волна называется монохроматической.

Для описания распространения волновых процессов вводят следующие характеристики. Аргумент косинуса (см. формулу (3.2)), т.е. выражение , называетсяфазой волны.

Схематически распространение волны вдоль одной координаты показано на рис. 3.2, в данном случае распространение происходит вдоль оси z.

Рис. 3.2 Определение длины волны

Период – время одного полного колебания. Период обозначается буквой Т и измеряется в секундах (с). Величина обратная периоду называется линейной частотой и обозначается f , измеряется в герцах (=Гц). Линейная частотаf связана с круговой частотой ω. Связь выражается формулой

. (3.3)

Если зафиксировать время t, то из рис. 3.2 видно, что существуют точки, например А и В, которые колеблются одинаково, т.е. в фазе (синфазно). Расстояние между ближайшими двумя точками, колеблющимися в фазе, называется длиной волны. Обозначается длина волны l и измеряется в метрах (м).

Волновое число b и длина волны l связаны между собой формулой

. (3.4)

Волновое число b иначе называют фазовой постоянной или постоянной распространения. Из формулы (3.4) видно, что постоянная распространения измеряется в (). Физический смысл заключается в том, что она показывает, на сколько радиан изменяется фаза волны при прохождении одного метра пути.

Для описания волнового процесса вводят понятие фронта волны. Фронт волны – это геометрическое место воображаемых точек поверхности, до которых дошло возбуждение. Фронт волны иначе называют волновым фронтом.

Уравнение, описывающее волновой фронт плоской волны, получают из уравнения (3.2), в виде

. (3.5)

Формула (3.5) выражают уравнение волнового фронта плоской волны. Уравнение (3.4) показывает, что волновые фронты представляют собой бесконечные плоскости, перемещающиеся в пространстве перпендикулярно оси z.

Скорость перемещения фазового фронта называется фазовой скоростью. Фазовая скорость обозначается V_ф и определяется формулой

. (3.6)

Первоначально уравнение (3.2) содержит фазу с двумя знаками – отрицательным и положительным. Отрицательный знак, т.е. , указывает, что фронт волны распространяется вдоль положительного направления распространения осиz. Такая волна называется бегущей, или падающей.

Положительный знак фазы волны указывает на движение фронта волны в обратном направлении, т.е. противоположном направлению оси z. Такая волна называется отраженной.

В дальнейшем будем рассматривать бегущие волны.

Если волна распространяется в реальной среде, то из-за происходящих тепловых потерь, неизбежно происходит уменьшение амплитуды. Рассмотрим пример. Пусть волна распространяется вдоль оси z и первоначальное значение амплитуды волны соответствует 100%, т.е. A₀=100. Допустим, при прохождении одного метра пути, амплитуда волны уменьшается на 10%. Тогда будем иметь следующие значения амплитуд волн

Общая закономерность изменения амплитуды имеет вид

Такими свойствами обладает показательная функция. Графически процесс можно показать в виде рис. 3.3.

Рис. 3.3 Уменьшение амплитуды при распространении волны в среде

В общем виде соотношение пропорциональности запишем как

, (3.7)

где a - постоянная затухания волны.

Фазовую постоянную b и постоянную затухания a объединяют с помощью введения комплексной постоянной распространения g, т.е.

, (3.8)

где b - фазовая постоянная, a - постоянная затухания волны.

В зависимости от вида волнового фронта различают волны плоские, сферические, цилиндрические.

Плоская волна – это волна, имеющая плоский фронт волны. Плоской волне можно дать следующее определение. Волна называется плоской однородной, если векторное поле ив любой точке плоскости перпендикулярны направлению распространения и не изменяются по фазе и амплитуде.

Уравнение плоской волны

. (3.9)

Если источник, порождающий волну, является точечным, то фронт волны, распространяющийся в неограниченном однородном пространстве, представляет собой сферу. Сферическая волна – это волна, имеющая сферический фронт волны. Уравнение сферической волны имеет вид

, (3.10)

где r – радиус-вектор, проведенный из начала координат, совпадающего с положением точечного источника, в конкретную точку пространства, расположенной на расстоянии r.

Волны могут возбуждаться с помощью бесконечной нити источников, расположенных вдоль оси z. В этом случае такая нить будет порождать волны, фазовый фронт которых представляет собой цилиндрическую поверхность.

Цилиндрическая волна – это волна, имеющая фазовый фронт в виде цилиндрической поверхности. Уравнение цилиндрической волны имеет вид

, (3.11)

Формулы (3.2), (3.10, 3.11) указывают на различную зависимость амплитуды от расстояния между источником волны и конкретной точкой пространства, до которой дошла волна.

1. Уравнения Гельмгольца

Максвелл доказал, что распространение электромагнитных процессов в пространстве с течением времени происходит в виде волны. Рассмотрим доказательство этого положения, т.е. докажем волновой характер электромагнитного поля.

Запишем первые два уравнения Максвелла в комплексной форме в виде

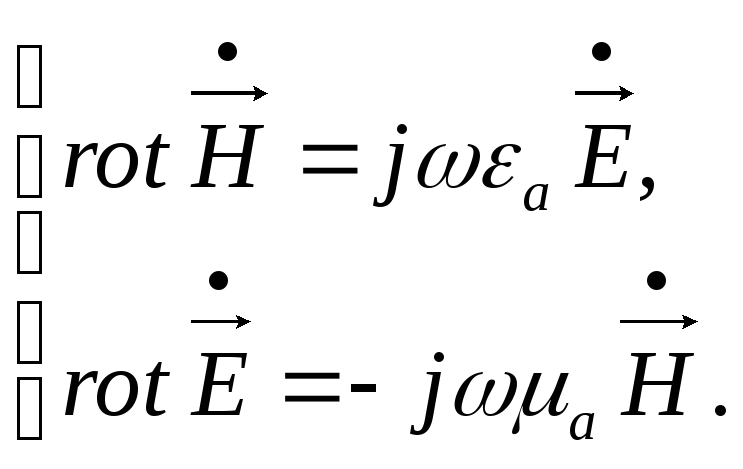(3.12)

Возьмем второе уравнение системы (3.12) и применим к нему операцию ротора к левой и правой частям. В результате получим

. (3.13)

Обозначим , представляющую собой постоянную распространения. Таким образом, имеем

. (3.14) С другой стороны, на основе известного тождества в векторном анализе запишем

, (3.15)

где является оператором Лапласа, который в декартовой системе координат выражается тождеством

(3.16)

Учитывая закон Гаусса, т.е. , уравнение (3.15) запишется упрощенном виде

, или

. (3.17)

Аналогично, пользуясь симметрией уравнений Максвелла, можно получить уравнение относительно вектора , т.е.

. (3.18)

Уравнения вида (3.17, 3.18) называются уравнениями Гельмгольца. В математике доказано, что если какой-либо процесс описывается в виде уравнений Гельмгольца, то это означает, что процесс является волновым процессом. В нашем случае делаем заключение: переменные во времени электрическое и магнитное поле неизбежно приводит к распространению в пространстве электромагнитных волн.

В координатной форме уравнение Гельмгольца (3.17) записывают в виде

, (3.19)

где ,,- единичные векторы вдоль соответствующих осей координат,

или

,

, (3.20)

.

2. Свойства плоских волн при распространении в не поглощающих средах

Пусть плоская электромагнитная волна распространяется вдоль оси z, тогда распространение волны описывается системой дифференциальных уравнений

(3.21)

где и- комплексные амплитуды поля,

. (3.22)

Решение системы (3.21) имеет вид

(3.23)

Если волна распространяется только в одном направлении вдоль оси z, и вектор направлен вдоль осиx, то решение системы уравнений целесообразно записать в виде

(3.24)

где и- единичные орты вдоль осиx,y.

Если в среде отсутствуют потери, т.е. параметры среды e_а и m_а, и являются действительными величинами.

Перечислим свойства плоских электромагнитных волн

1. Для среды вводится понятие волнового сопротивления среды

, (3.25)

где ,- амплитудные значения напряженностей поля. Волновое сопротивление для среды без потерь также является действительной величиной.

Для воздуха волновое сопротивление составляет

. (3.26)

2. Из уравнения (3.24) видно, что магнитное и электрическое поля совпадают по фазе. Поле плоской волны представляет собой бегущую волну, которую записывается в виде

(3.27)

Рис. 3.4 Распространение плоской электромагнитной волны

На рис. 3.4 векторы поля иизменяются синфазно, как следует из формулы (3.27).

3. Вектор Пойнтинга в любой момент времени совпадает с направлением распространения волны

. (3.28)

Модуль вектора Пойнтинга определяет плотность потока мощности и измеряется в .

4. Средняя плотность потока мощности определяется

(3.29)

или

, (3.30)

где - действующие значения напряженностей поля.

Энергия поля, заключенная в единице объема, называется плотностью энергии. Электромагнитное поле изменяется с течением времени, т.е. является переменным. Значение плотности энергии в данный момент времени называется мгновенной плотностью энергии. Для электрической и магнитнойсоставляющих электромагнитного поля мгновенные плотности энергии соответственно равны

, (3.31)

. (3.32)

Учитывая, что , из соотношений (3.31) и (3.32) видно, что.

Полная плотность электромагнитной энергииопределяется выражением

. (3.33)

1. Фазовая скорость распространения электромагнитной волны определяется формулой

. (3.34)

2. Длина волны λ определяется

, (3.35)

где - длина волны в вакууме (воздухе), с – скорость света в воздухе,e - относительная диэлектрическая проницаемость, m - относительная магнитная проницаемость, f – линейная частота, w - циклическая частота, V_ф – фазовая скорость, b - постоянная распространения.

3. Скорость перемещения энергии (групповая скорость ) можно определить из формулы

, (3.36)

где - вектор Пойнтинга,v - плотность электромагнитной энергии.

Если расписать иv в соответствие с формулами (3.28), (3.33), то получим

. (3.37)

Таким образом, получим соотношение

. (3.38)

При распространении электромагнитной монохроматической волны в среде без потерь выполняется равенство фазовой и групповой скорости.

Между фазовой и групповой скоростью существует связь, выраженная формулой

. (3.39)

Рассмотрим пример распространения электромагнитной волны во фторопласте, имеющем параметры e =2, m=1. Пусть напряженность электрического поля соответствует

(3.40)

Скорость распространения волны в такой среде будет равна

.(3.41)

Волновое сопротивление в среде из фторопласта соответствует значению

Ом. (3.42)

Амплитудные значения напряженности магнитного поля принимают значения

, . (3.43)

Плотность потока энергии, соответственно, равна

. (3.44)

Длина волны на частоте имеет значение

. (3.45)

4. Теорема Умова – Пойнтинга

Электромагнитное поле характеризуется собственной энергией поля, причем, полная энергия определяется суммой энергий электрического и магнитного полей. Пусть электромагнитное поле занимает замкнутый объем V. Тогда можно записать

. (3.46)

Энергия электромагнитного поля, в принципе, не может оставаться постоянной величиной. Возникает вопрос: какие факторы влияют на изменение энергии? Установлено, что на изменение энергии внутри замкнутого объема влияют следующие факторы:

• часть энергии электромагнитного поля может превратиться в другие виды энергии, например, механическую;

• внутри замкнутого объема могут действовать сторонние силы, которые способны увеличивать или уменьшать энергию электромагнитного поля, заключенную в рассматриваемом объеме;

• рассматриваемый замкнутый объем V обменивается энергией с окружающими телами за счет процесса излучения энергии.

Интенсивность излучения характеризуется вектором Пойнтинга. ОбъемV имеет замкнутую поверхность S. Изменение энергии электромагнитного поля рассматривают как поток вектора Пойнтинга сквозь замкнутую поверхность S (рис. 3.5), т.е. , причем возможны варианты>0, <0, =0. Отметим, что нормаль, проведенная к поверхности ,всегда является внешней.

S

Рис. 3.5 Излучение энергии из объема V

Напомним, что , где-это мгновенные значения напряженности поля.

(3.47)

Переход от интеграла по поверхности к интегралу по объему V осуществлен на основе теоремы Остроградского-Гаусса.

Зная, что подставим эти выражения в формулу (3.47). После преобразования, получим выражение в виде:

.(3.48)

Из формулы (3.48) видно, что левая часть выражается суммой, состоящей из трех слагаемых, каждое из которых рассмотрим в отдельности.

Слагаемое выражаетмгновенную мощность потерь, обусловленную в рассматриваемом замкнутом объеме токами проводимости. Иными словами, слагаемое выражает тепловые потери энергии поля, заключенного в замкнутом объеме.

Второе слагаемое выражает работу сторонних сил, произведенную в единицу времени, т.е. мощность сторонних сил. Для такой мощности возможны значения >0, <0.

Если >0, т.е. в объеме V добавляется энергия, тогда сторонние силы можно рассматривают в качестве генератора. Если <0, т.е. в объеме V происходит уменьшение энергии, то сторонние силы играют роль нагрузки.

Последнее слагаемое для линейной среды представим в виде:

(3.49)

Формула (3.49) выражает скорость изменения энергии электромагнитного поля, заключенного внутри объема V.

После рассмотрения всех слагаемых можно формулу (3.48) запишем в виде:

.(3.50)

Формула (3.50) выражает собой теорему Пойнтинга. Теорема Пойнтинга выражает баланс энергии внутри произвольной области, в которой существует электромагнитное поле.

4. Запаздывающие потенциалы

Запишем уравнения Максвелла в комплексной форме:

(3.51)

Пусть в однородной среде существуют сторонние токи. Попробуем преобразовать уравнения Максвелла для такой среды и получить более простое уравнение, описывающее электромагнитное поле в ней.

Возьмем уравнение .Зная, что характеристики и связаны между собой,то можно записать Учтем, что напряженность магнитного поля можно выразить с помощью векторного электродинамического потенциала , который вводится соотношением , тогда

. (3.52)

Возьмем второе уравнение системы Максвелла (3.51) и выполним преобразования:

т.е.

(3.53)

Формула (3.53) выражает второе уравнение Максвелла через векторный потенциал . Формулу (3.53) можно записать в виде

или

(3.54)

В электростатике, как известно, выполняется соотношение:

(3.55)

где -вектор напряженности поля, - скалярный электростатический потенциал. Знак минус указывает, что вектор направлен из точки, имеющей более высокий потенциал, в точку с более низким потенциалом.

Выражение в скобках (3.54) по аналогии с формулой (3.55) запишем в виде

или

(3.56)

где - скалярный электродинамический потенциал.

Возьмем первое уравнение Максвелла и запишем его с помощью электродинамических потенциалов

или

или

(3.57)

В векторной алгебре доказано тождество:

(3.58)

Используя тождество (3.58) можно первое уравнение Максвелла, записанное в виде (3.57), представить в виде

или

Приведем подобные

Умножим левую и правую части на множитель (-1):

(3.59)

можно задать произвольным образом, поэтому можно положить, что

. (3.60)

Выражение (3.60) называется лоренцевой калибровкой.

Если w=0, то получим кулонову калибровку =0.

С учетом калибровок уравнение (3.59) можно записать

. (3.61)

Уравнение (3.61) выражает собой неоднородное волновое уравнение для векторного электродинамического потенциала.

Аналогичным путем, исходя из третьего уравнения Максвелла ,можно получить неоднородное уравнение для скалярного электродинамического потенциала в виде:

(3.62)

Полученные неоднородные уравнения для электродинамических потенциалов имеют свои решения в виде

, (3.63)

гдеМ – произвольная точка М, -объемная плотность заряда, γ – постоянная распространения, r – текущее расстояние от каждого элемента объема источника до точки М.

, (3.64)

где V – объем, занимаемый сторонними токами, r – текущее расстояние от каждого элемента объема источника до точки М.

Решение для векторного электродинамического потенциала (3.63), (3.64) называется интегралом Кирхгофа для запаздывающих потенциалов.

Множитель с учетом выразим в виде

Этот множитель соответствует конечной скорости распространения волны от источника, причем Т.к. скорость распространения волны является конечной величиной, то воздействие источника, порождающего волны, до произвольной точки М доходит с запаздыванием во времени. Значение времени запаздывания определяется:На рис. 3.6 показан точечный источникU, который излучает сферические волны, распространяющиеся со скоростью v в окружающем однородном пространстве, а также произвольная точка М, расположенная на расстоянии r, до которой доходит волна.

Рис. 3.6 Излучение энергии точечным источником

В момент времени t векторный потенциал в точке М является функцией токов, протекающих в источнике U в более раннее время Иными словами,зависит от токов источника, которые протекали в ней в более ранний момент

Из формулы (3.64) видно, что векторный электродинамический потенциал параллелен (сонаправлен) плотности тока сторонних сил; его амплитуда убывает по закону ; на больших расстояниях по сравнению с размерами излучателя волна имеет сферический фронт волны.

Учитывая и первое уравнение Максвелла, определим напряженность электрического поля:

(3.65)

Полученные соотношения определяют электромагнитное поле в пространстве, созданном заданным распределением сторонних токов

4. Распространение плоских электромагнитных волн в хорошо проводящих средах

Рассмотрим распространение электромагнитной волны в проводящей среде. Такие среды также называют металлоподобными. Реальная среда является проводящей, если плотность токов проводимости значительно превосходит плотность токов смещения, т.е.и, причем, или

. (3.66)

Формула (3.66) выражает условие, при котором реальную среду можно считать проводящей. Иными словами, мнимая часть комплексной диэлектрической проницаемости должна превосходить действительную часть. Формула (3.66) также показывает зависимость от частоты. Причем, чем ниже частота, тем в среде более ярко выражены свойства проводника. Рассмотрим пример. Так, на частотеf = 1МГц = 10⁶ Гц сухая почва имеет параметры e=4, s=0,01,. Сравним между собойи, т.еи. Из полученных значений видно, что 1,6×10^-9 >> 3,56×10^-11, поэтому сухую почву при распространении волны с частотой 1 МГц следует считать проводящей.

Для реальной среды запишем комплексную диэлектрическую проницаемость

. (3.67)

В нашем случае , поэтому для проводящей среды следует записать

. (3.68)

Постоянная распространения g, как известно, определяется из уравнений Гельмгольца

.

Таким образом, получим формулу для постоянной распространения

. (3.69)

Известно, что

. (3.70)

Учитывая тождество (3.49), формулу (3.50) запишем в виде

. (3.71)

Постоянная распространения выражается в виде

. (3.72)

Сравнение действительных и мнимых частей в формулах (3.71), (3.72) приводит к равенству значений фазовой постоянной b и постоянной затухания a, т.е.

. (3.73)

Из формулы (3.73) выпишем длину волны, которую приобретает поле при распространении в хорошо проводящей среде

, (3.74)

где - длина волны в металле.

Из полученной формулы (3.74) видно, что длина электромагнитной волны, распространяющейся в металле, значительно сокращается по сравнению с длиной волны в пространстве.

Выше сказано, что амплитуда волны при распространении в среде с потерями уменьшается по закону . Для характеристики процесса распространения волны в проводящей среде введено понятиеглубины поверхностного слоя или глубины проникновения.

Глубина поверхностного слоя - это расстояние d, на котором амплитуда поверхностной волны уменьшается в е раз по сравнению с ее начальным уровнем.

, (3.75)

где - длина волны в металле.

Глубину поверхностного слоя также определяют из формулы

, (3.76)

где w - циклическая частота, m_а – абсолютная магнитная проницаемость среды, s - удельная проводимость среды.

Из формулы (3.76) видно, что с повышением частоты и удельной проводимости, глубина поверхностного слоя уменьшается.

Приведем пример. Медь с удельной проводимостью на частотеf = 10 ГГц (l = 3см) имеет глубину поверхностного слоя d = . Отсюда сделаем важный для практики вывод: нанесение на непроводящее покрытие слоя хорошо проводящего вещества позволит выполнить элементы устройств с малыми тепловыми потерями.

4. Отражение и преломление плоской волны на границе раздела сред

При распространении плоской электромагнитной волны в пространстве, представляющем собой области с различными значениями параметров и границей раздела двух сред в виде плоскости, возникают отраженные и преломленные волны. Интенсивности этих волн определяют через коэффициенты отражения и преломления.

Коэффициентом отражения волны называется отношение комплексных значений напряженностей электрического поля отраженной к падающей волн на границе раздела и определяется формулой:

, (3.77)

Коэффициентом прохождения волны во вторую среду из первой называется отношение комплексных значений напряженностей электрического поля преломленной к падающейволн и определяется формулой

. (3.78)

Если вектор Пойнтинга падающей волны перпендикулярен границе раздела, то

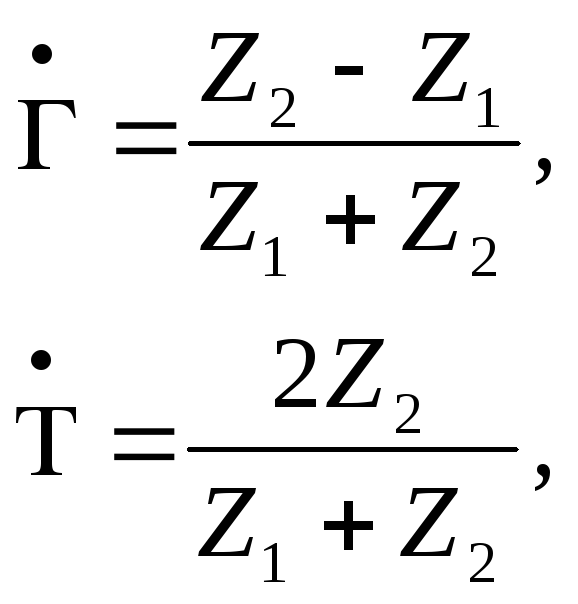(3.79)

где Z₁,Z₂ – характеристическое сопротивление соответствующих сред.

Характеристическое сопротивление определяется по формуле:

где , (3.80)

.

При наклонном падении направление распространения волны по отношению к границе раздела задается углом падения. Угол падения – угол между нормалью к поверхности и направлением распространения луча.

Плоскость падения – это плоскость, которая содержит падающий луч и нормаль, восстановленную в точку падения.

Из граничных условий следует, что углы падения и преломления связаны законом Снелля:

, (3.81)

где n₁, n₂ - показатели преломления соответствующих сред.

Электромагнитные волны характеризуются поляризацией. Различают эллиптическую, круговую и линейную поляризации. В линейной поляризации выделяют горизонтальную и вертикальную поляризацию.

Горизонтальная поляризация – поляризация, при которой вектор колеблется в плоскости, перпендикулярной плоскости падения.

Пусть на границу раздела двух сред падает плоская электромагнитная волна с горизонтальной поляризацией (рис. 3.7). Вектор Пойнтинга падающей волны обозначен . Т.к. волна имеет горизонтальную поляризацию, т.е. вектор напряженности электрического поля колеблется в плоскости, перпендикулярной плоскости падения, то он обозначени на рис. 3.7 показан в виде кружочка с крестиком (направлен от нас). Соответственно вектор напряженности магнитного поля лежит в плоскости падения волны и обозначен. Векторы,,образуют правую тройку векторов.

Для отраженной волны соответствующие векторы поля снабжены индексом «отр», для преломленной индексом - «пр».

При горизонтальной (перпендикулярной) поляризации нахождение коэффициентов отражения и прохождения находят следующим образом (рис. 3.7).

Рис. 3.7 Падение волны с горизонтальной поляризацией на границу раздела сред

На границе раздела двух сред выполняются граничные условия, т.е.

В нашем случае мы должны выявить тангенциальные проекции векторов, т.е. соответственно запишем

Линии напряженности магнитного поля направлены для падающей, отраженной и преломленной волн перпендикулярно плоскости падения. Поэтому следует записать

.

Исходя из этого, составим на основании граничных условий систему

,

Известно, что напряженности электрического и магнитного полей связаны между собой через волновое сопротивление среды Z

.

Тогда второе уравнение системы запишем в виде

.

Итак, система уравнений приобрела вид

Разделим оба уравнения этой системы на амплитуду падающей волны и,учитывая определения коэффициентов преломления (3.77) и прохождения (3.78), запишем систему в виде

Система имеет два решения и две неизвестные величины. Такая система разрешима.

(3.82)

Вертикальная поляризация – поляризация, при которой вектор колеблется в плоскости падения.

При вертикальной (параллельной) поляризации коэффициенты отражения и прохождения выражаются следующим образом (рис. 3.8).

1 среда

2 среда

Рис. 3.8 Падение волны с вертикальной поляризацией на границу раздела сред

Для вертикальной поляризации записывают аналогичную систему уравнений с учетом направления векторов электромагнитного поля

Такую систему уравнений аналогичным образом можно привести к виду

Решением системы являются выражения для коэффициентов отражения и прохождения

(3.83)

При падении плоских электромагнитных волн с параллельной поляризацией на границу раздела двух сред коэффициент отражения может обращаться в ноль. Угол падения, при котором падающая волна полностью, без отражения, проникает из одной среды в другую, называется углом Брюстера и обозначается как .

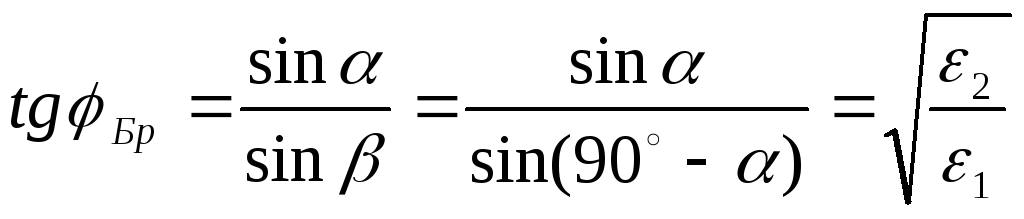, (3.84)

или угол Брюстера определяют из формулы

. (3.85)

Подчеркнем, что угол Брюстера при падении плоской электромагнитной волны на немагнитный диэлектрик может существовать лишь при параллельной поляризации.

Если плоская электромагнитная волна падает под произвольным углом на границу раздела двух сред с потерями, то отраженную и преломленную волны следует считать неоднородными, так как плоскость равных амплитуд должна совпадать с границей раздела. Для реальных металлов угол между фазовым фронтом и плоскостью равных амплитуд мал, поэтому можно полагать, что угол преломления равен 0.

8. Приближенные граничные условия Щукина-Леонтовича

Данные граничные условия применимы в случае, если одна из сред является хорошим проводником. Предположим, что плоская электромагнитная волна падает под углом j из воздуха на плоскую границу раздела с хорошо проводящей средой, которая описывается комплексным показателем преломления

. (3.86)

Из определения понятия хорошо проводящей среды следует, что . Применив закон Снелля, можно отметить, что угол преломленияb будет очень малым. Поэтому можно считать, что преломленная волна входит внутрь хорошо проводящей среды практически по направлению нормали при любом значении угла падения.

Используя граничные условия Леонтовича, необходимо определить касательную составляющую магнитного вектора . Обычно приближенно полагают, что эта величина совпадает с аналогичной составляющей, вычисленной на поверхности идеального проводника. Ошибка, возникающая при таком приближении, будет очень мала, так как коэффициент отражения от поверхности металлов, как правило, близок к нулю.

8. Излучение электромагнитных волн в свободное пространство

Выясним, в чем состоят условия излучения электромагнитной энергии в свободное пространство. Для этого рассмотрим точечный монохроматический излучатель электромагнитных волн, который помещен в начало сферической системы координат. Как известно, сферическая система координат задается (r, Θ, φ), где r – радиус вектор, проведенный из начала системы координат в точку наблюдения; Θ – меридиональный угол, отсчитываемый от оси z (зенита) до радиус-вектора, проведенного в точку М; φ – азимутальный угол, отсчитываемый от оси Х до проекции радиус-вектора, проведенной из начала координат до точки М′ (М′ - это проекция точки М на плоскость xoy) (рис.3.9).

Рис. 3.9. Положение точки М в сферической системе координат

Точечный излучатель находится в однородной среде, обладающей параметрами

Такой источник излучает электромагнитные волны во все направления и любая составляющая электромагнитного поля подчиняется уравнению Гельмгольца, кроме точки r=0. Можно ввести комплексную скалярную функцию Ψ, под которой понимают любую произвольно взятую составляющую поля. Тогда уравнение Гельмгольца для функции Ψ имеет вид:

, (3.87)

где - волновое число (постоянная распространения).

Постоянную распространения выразим в виде

(3.88)

Положим, что функция Ψ обладает сферической симметрией, тогда уравнение Гельмгольца запишем в виде:

(3.89)

Запись уравнение (3.89) можно несколько видоизменить:

(3.90)

Уравнения (3.89) и (3.90) являются тождественными между собой. Уравнение (3.90) известно в физике как уравнение колебаний. Такое уравнение имеет два решения, которые при равенстве амплитуд имеют вид:

(3.91)

(3.92)

Как видно из (3.91), (3.92) решение уравнения отличается только знаками. Причем, указывает набегущую волну от источника, т.е. волну распространяющуюся от источника в бесконечность. Вторая функция указывает, что волна приходит к источнику из бесконечности. Физически один и тот же источник не может порождать одновременно две волны: бегущую и приходящую из бесконечности. Поэтому необходимо учесть, что волна физически не существует.

Рассматриваемый пример достаточно прост. В случае излучения энергии системой источников выбрать правильное решение весьма сложно. Поэтому требуется аналитическое выражение, являющееся критерием выбора правильного решения. Нужен общий критерий в аналитическом виде, позволяющий выбрать однозначное физически обусловленное решение.

Иными словами, нужен такой критерий, который отличает функцию, выражающую собой волну, бегущую от источника в бесконечность, от функции, описывающей волну, приходящую из бесконечности в источник излучения.

Такая задача решена А. Зоммерфельдом. Он показал, что для бегущей волны, описываемой функцией ,выполняется соотношение:

(3.93)

Эта формула называется условием излучения или условием Зоммерфельда.

Рассмотрим элементарный электрический излучатель в виде диполя. Электрический диполь представляет собой отрезок провода малой длины l по сравнению с длиной волны l (l << l), по которому протекает переменный ток (рис. 3.10). Т.к. выполняется условие l << l, то можно считать, что во всех сечениях провода в данный момент времени протекает одинаковый по велечине ток

Рис. 3.10 Излучающий диполь

Нетрудно показать, что изменение электрического поля в пространстве окружающем провод, носит волновой характер. Для наглядности рассмотрим предельно упрощенную модель процесса образования и изменения электрической составляющей электромагнитного поля, которую излучает провод. На рис. 3.11 показана модель процесса излучения электрического поля электромагнитной волны в течение времени, равного одному периоду.

Рис.3.11 Модель процесса излучения за один период

Как известно, электрический ток i обусловлен движением электрических зарядов и можно записать

или .

В дальнейшем будем рассматривать только изменение на проводе положения положительного и отрицательного зарядов. Силовая линия напряженности электрического поля начинается на положительном заряде и оканчивается на отрицательном. На рис. 3.11 силовая линия показана пунктиром. Помним, что электрическое поле создается во всем пространстве, окружающем проводник, хотя на рис. 3.11 показана одна силовая линия.

Чтобы по проводнику протекал переменный ток, необходим источник переменной ЭДС. Такой источник включен в середину провода. Состояние процесса излучения электрического поля показано на рис. 3.11 цифрами от 1 до 13. Каждая цифра соответствует определенному моменту времени, соответствующему состоянию процесса. Момент времени t=1 соответствует началу процесса, т.е. ЭДС = 0. В момент t=2 появляется переменная ЭДС, которая вызывает движение зарядов. С появлением движущихся зарядов в проводе возникает электрическое поле в пространстве. С течением времени (t = 3÷5) заряды движутся к концам проводника и силовая линия охватывает все большую часть пространства. Силовая линия расширяется со скоростью света в направлении, перпендикулярном проводу. В момент времени t = 6 – 8 ЭДС, пройдя через максимальное значение, уменьшается. Заряды движутся к середине провода.

В момент времени t = 9 заканчивается полупериод изменения ЭДС, она уменьшается до нуля. При этом происходит слияние зарядов, они компенсируют друг друга. Электрическое поле в этом случае отсутствует. Силовая линия напряженности излученного электрического поля замыкается и продолжает удаляться от провода.

Далее наступает второй полупериод изменения ЭДС, процессы повторяются с учетом изменения полярности. В моменты t = 10÷13 показана картина протекания процесса с учетом силовой линии напряженности электрического поля.

Мы рассмотрели процесс образования замкнутых силовых линий вихревого электрического поля. Стоит помнить, что излучение электромагнитных волн является единым процессом. Электрическое и магнитное поле являются неразрывными взаимообусловленными составляющими электромагнитного поля.

Процесс излучения, показанный на рис. 3.11, аналогичен излучению электромагнитного поля симметричным электрическим вибратором, который широко применяется в технике радиосвязи. Необходимо помнить, что плоскость колебаний вектора напряженности электрического поля является взаимно перпендикулярной плоскости колебаний вектора напряженности магнитного поля.

Излучение электромагнитных волн обусловлено переменным процессом. Поэтому в формуле для заряда можно положить постоянную С=0. Для комплексной величины заряда можно запишем:

. (3.94)

По аналогии с электростатикой введем понятие момента электрического диполя с переменным током :

. (3.95)

Из формулы (3.95) следует, что векторы момента электрического диполя и направленного отрезка провода являются сонаправленными.

Заметим, что реальные антенны имеют длину проводов обычно сравнимую с длиной волны. Чтобы определить излучательные характеристики таких антенн, провод мысленно разбивают на отдельные малые участки, каждый из которых рассматривают в виде элементарного электрического диполя. Результирующее поле антенны находят путем суммирования излучаемых векторных полей, порожденных отдельными диполями.