2.2. Методы (способы) представления колебаний

Колебательный процесс можно представить аналитически, временной диаграммой (т.е. графиком зависимости колеблющейся динамической переменной от времени), спектральной диаграммой, векторной диаграммой, фазовой траекторией (диаграммой состояния).

а. Аналитически гармонические колебания выражаются уравнением колебаний с использованием тригонометрических функций синуса или косинуса. Например:

x(t) = A cos(t + ).

В соответствии с соотношением Эйлера =cos + i sin гармонические колебания аналитически можно представить и в комплексном пространстве (здесь i = ). Под гармонической функцией в комплексном пространстве следует понимать экспоненту с мнимым показателем:x(t) = A

б. Гармонические колебания, например, напряжения в колебательном контуре U(t) = U₀ cos(t + ), можно представить графически временной диаграммой, т.е. графиком U(t), где по горизонтальной оси отложено время t, по вертикальной оси колеблющаяся динамическая переменная U (см. рис. 5). Эта диаграмма может быть получена с помощью осциллографа, подключенного, например, к активному сопротивлению колебательного контура.

Рис. 5.

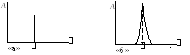в. Если фазовые характеристики (фазовые соотношения) не интересны, то колебание удобно представлять графически спектральной диаграммой. На графике по горизонтальной оси откладывается частота  (или  =), а по вертикали амплитуда динамической переменной (или энергия, пропорциональная квадрату амплитуды и частоты). В случае гармонического колебания x(t) = A cos(t + ) спектр состоит из одной частоты  (рис. 6-а). В реальной колебательной системе в ее спектре содержатся набор частот в определенном частотном диапазоне (рис.6-б).

Рис. 6.

г. Гармонические колебания можно представить векторной диаграммой. Гармоническое колебание x(t) = A cos(t + ) определено, если заданы амплитуда А, начальная фаза  и циклическая частота . Эти характеристики на векторной диаграмме выражаются следующим образом. Выбирается полюс 0 и луч ОМ (см. рис. 7). Относительно луча ОМ отсчитывается начальная фаза. Из полюса проводится вектор А, модуль которого рав

Рис.7

ен амплитуде колебания, причем векторА поворачивается на угол , равный начальной фазе колебания (положительный угол соответствует повороту против часовой стрелки, отрицательный – против). Предполагается, что вектор А вращается относительно полюса 0 с угловой скоростью . Таким образом, векторная диаграмма отображает все характеристики уравнения колебаний.

д. Представление колебательного процесса с помощью фазовой траектории (диаграммы состояния). Этот способ рассмотрим на примере механической колебательной системы. Известно, что состояние и изменение состояния любой механической системы материальных точек с их известными массами полностью определено, если в данный момент времени одновременно заданы координаты и скорости всех материальных точек механической системы (в теоретическом курсе классической механики состояние системы задается координатами и импульсом). Пусть смещение материальной точки, прикрепленной к пружине, совершается по закону x(t) = A cos(t + ), тогда скорость материальной точки изменяется по закону v_x = . Возведя в квадрат эти уравнения и принимая во внимание тождество cos² (t + ) + sin² (t + ) = 1, получим:

+ = 1 или x² + =A².

Последнее уравнение - это уравнение окружности радиусаА (рис.8). Изображающая точка, т.е. точка на графике, изображающая состояние колебательной системы, движется равномерно по окружности по часовой стрелке. Изобра-

Рис.8. Рис.9. жающая точка при движении образует фазовую траекторию. Если колебание гармоническое, то фазовая траектория представляет собой замкнутую кривую.

Фазовая траектория затухающих колебаний имеет вид спирали, скручивающейся к началу 0. Действительно, уравнение для смещения затухающих колебаний имеет вид:

x(t) = A cos t (для простоты за начальную фазу принято значение  = 0).

Уравнение скорости v_x = =  A( cos t +  sin t). При малых затуханиях (<<) v_x = A sin t. Возведя в квадрат уравнения для смещения и скорости, получим:

x² + =A². Это уравнение спирали, скручивающейся к началу 0, т.е. к состоянию равновесия колебательной системы с нулевой координатой и нулевой скоростью (рис. 9).