2.11. Спектр атома водорода

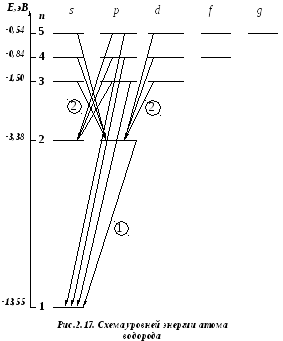
Изобразим схему уровней энергии атома водорода (рис.2.17).

Испускание и поглощение света происходит при переходе электрона с одного энергетического уровня на другой. В квантовой механике доказывается, что наиболее вероятны (возможны) только такие переходы, при которых изменение квантового числа lравно

. (2.87)

Это условие называется правилом отбора.

При переходе электронов излучается квант энергии, равный

. (2.88)

Здесь - энергия уровня, соответствующего значению главного квантового числаn_i,ν – частота,λ– длина волны излучения. Формулу (2.88) можно представить в виде:

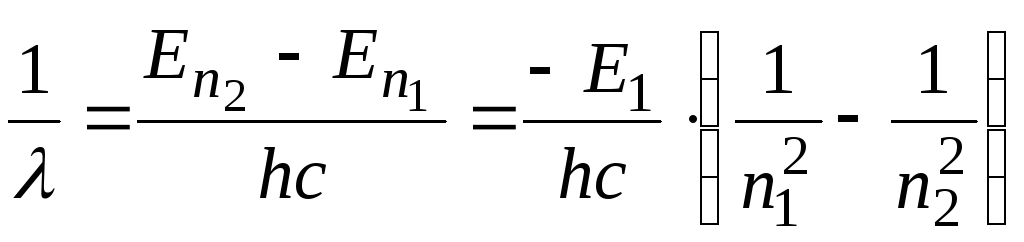, (2.89)

где .

Группа спектральных линий с одинаковыми называетсясерией. Назовем некоторые серии линий спектра атомов водорода:

–серия Лаймана, она находится в ультрафиолетовой части спектра.

–серия Бальмера, она находится в видимой части спектра.

- серия Пашена, она находится в инфракрасной части спектра.

На рис.2.17 изображены электронные переходы, соответствующие сериям Лаймана (1) и Бальмера (2) с учетом правил отбора (2.87).

Формулу (2.89) можно записать в виде

, (2.90),

где . (2.91)

Выражение (2.90) называется сериальной формулой. Величина R называется постоянной Ридберга; ранее она была установлена экспериментально, ее численное значение равно , что совпадает с вычисленным по формуле (2.90).

2.12. Распpеделение электpонов в атоме по энеpгетическим состояниям. Пеpиодическая система элементов д.И.Менделеева

В 1869 году Д.И.Менделеев открыл периодический закон, согласно которому химические и некоторые физические свойства элементов зависят от их масс. Основы теории пеpиодической системы элементов были разработаны гораздо позже с квантовых позиций.

Квантовая теория периодических изменений химических и физических свойств элементов построена на следующих предположениях.

• Порядковый номер элемента Zравен общему числу электронов в атоме данного элемента.

• Состояние электрона в атоме определяется набором четырех квантовых чисел: n , l , m, .

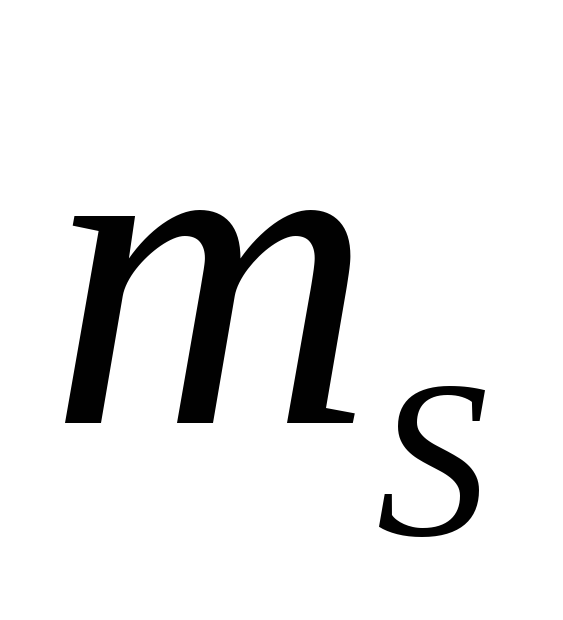• Распределение электронов в атоме по энергетическим состояниям должно удовлетворять принципу минимума потенциальной энергии. При возрастании числа электронов в атоме каждый последующий электрон занимает только состояние с наименьшей энергией.

• Заполнение энергетических состояний электронами в атоме должно подчиняться принципу Паули.

Из вышеизложенного следует: электроны в атоме могут занимать только определённые энергетические состояния. При этом химические и некоторые физические свойства элементов определяются валентными электронами атома.

Заполнение энергетических состояний подчиняется следующим принципам.

1. Все электроны в атомах, у которых одинаковы значения главного квантового числа n, образуютэлектронный слой. Максимальное число электронов в каждом слое определяется формулой:

. (2.92)

При n=1 (K - слой);

n=2 (L - слой);

n=3 (M - слой) и так далее.

В каждом слое электроны распределяются по оболочкам, каждой оболочке соответствует определённое значение орбитального квантового числа l.

2. Максимальное число электронов в оболочке определяется формулой:

, (2.93)

где число lможет принимать значения:l=0,1,2,…….n-1. Некоторые значенияи представлены в таблице 2.3.

Таблица 2.3

n	Слой
1	K	2	2
2	L	8	6
3	M	18	10

Электронные состояния в атоме принято обозначать символами.Например, основное состояние атома кислорода выражается следующими символами:1S², 2S², 2P⁴. Это означает, что в 1S- и 2S-состояниях находятся по два электрона, в 2P⁴-состоянии находятся четыре электрона.

В реальной периодической системе элементов имеются отступления от порядка заполнения энергетических состояний, который приведён в таблице. Такой порядок заполнения энергетических состояний имеет место в том случае, когда электронов в атоме не слишком много. При увеличении числа электронов в атоме на их энергию, кроме взаимодействия электронов с ядром, оказывает существенное влияние взаимодействие электронов между собой. Поэтому, если электронов в атоме много, то может оказаться, что состояние с большим nи малымl может быть для электрона более выгодно, чем состояние с малымnи большимl .

В квантовой механике показывается, что среднее расстояние электрона от ядра является периодической функцией времени. При переходе электрона из состояния nв состояниеm(n→m)среднее расстояние электрона определится выражением:

. (2.94)

Здесь и- волновые функции электрона в состоянииnиm.

Интеграл (2.94) при определённых условиях может обращаться в нуль; это означает, что переход электрона из состояния n в состояние m запрещён, и спектральной линии в этом случае не будет.

В квантовой механике существуют правила отбора,которые ограничивают число возможных переходов электронов в атоме.Возможны лишь такие переходы, при которых .

Волновые функции изависят от квантовых чисел: n, l, m, m_S .Расчёт показывает, что для электрона, движущегося в центрально-симметричном поле ядра^, при условии,что изменение орбитального квантового числа .

Примечание. Помимо правил отбора по орбитальному квантовому числу существуют и другие правила отбора, например, по магнитному квантовому числу. Их рассмотрение выходит за рамки данного пособия.