Условия максимумов и минимумов при интерференции световых волн

Поместим точечный источник монохроматического света на границе раздела двух сред с показателями преломленияи. Световая волна окажется разделенной на две волны (рис. ). В некоторой точке Р произойдёт наложение этих волн.

Уравнения возбуждаемых в точке Рколебаний имеют вид:

(1)

(2)

При сложении этих колебаний амплитуда результирующего колебания будет зависеть от разности фаз .

Разность фаз колебаний в точке Р

. (3)

Обозначим разность оптических путей

. (4)

Величина называетсяоптической разностью хода.

Отношение , (5)

где - длина световой волны в вакууме.

Из выражений (3), (4) и (5) следует связь между оптической разностью хода и разностью фаз колебаний:

. (6)

Если разность фаз колебаний

, (7)

то амплитуда имеет максимальное значение, будет наблюдаться интерференционный максимум.

Если разность фаз колебаний

, (8)

то амплитуда имеет минимальное значение, будет наблюдаться интерференционный минимум. Здесь - целое число.

Используя формулу (6) и выражения (7) и (8), можно записать и сформулировать условия интерференционных максимумов и минимумов для оптической разности хода.

Условие максимума: . (9)

Условие минимума: . (10)

Если оптическая разность хода равна четному числу длин полуволн, то будет наблюдаться интерференционный минимум, если нечетному - интерференционный максимум.

Интерференция в тонких пленках

При падении световой волны на тонкую прозрачную пластинку (плёнку) происходит отражение от обеих поверхностей пластинки. В результате возникают когерентные световые волны, которые могут интерферировать.

Получим условия интерференционных максимумов и минимумов для этого случая. Обозначим толщину пластинки символом , а показатель преломления её вещества -. Пусть на эту пластинку падает под угломплоская монохроматическая световая волна (луч света).

Л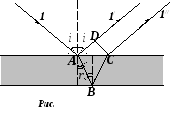уч света 1 в точке А частично отразится от верхней грани (1^/), частично преломится.

Преломленный луч испытывает отражение от нижней поверхности пластинки в точке В, затем, преломившись в точке С, под тем же углом iвыходит из пластинки (1^//).

Найдем оптическую разность хода лучей 1^/ и 1^//. Она равна

(1)

В этом выражении слагаемое учитывает изменение фазы световой волны напри её отражении от оптически более плотной среды (в точке.A).

Выразим оптическую разность хода через толщину пластинки, показатель преломленияи угол преломленияr . Учтем, что угол падения и угол преломления света связаны между собой соотношением:

(2)

Займемся геометрией (рис. )

(3)

; (4)

(5)

Подставим формулы (3) и (5) в выражение (1) для оптической разности хода, получим:

(6)

Так как , то

(7)

Оптическая разность хода зависит от толщины пленки , показателя преломления её материалаи длины световой волны.

Условием интерференционных максимумов будет выражение :

Условием интерференционных минимумов:

. (8)

Анализ полученных выражений позволяет сделать следующие выводы.

• Если на тонкую пленку постоянной толщины падает монохроматическое излучение, то в отраженном свете она будет либо окрашенной в один цвет, либо тёмной.

• Если толщина пленки неодинакова, то на ней будет наблюдаться интерференционная картина.

• Если плёнка постоянной толщины освещается белым светом, то она будет иметь окраску, соответствующую длине волны, для которой выполняется условие максимума.

• Если толщина пленки неодинакова, то при освещении белым светом она будет иметь участки, окрашенные в разные цвета.