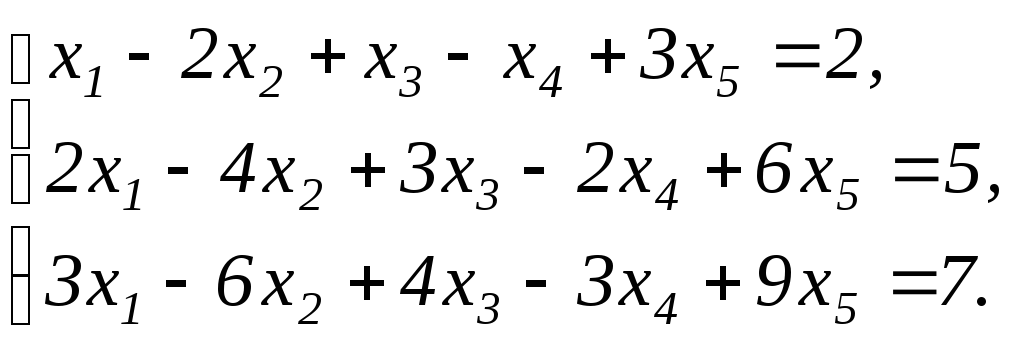- •Линейная алгебра
- •Основные вопросы программы раздела «линейная алгебра»
- •Решение типовых задач раздела
- •Задачи для самостоятельной и практической работы
- •Рейтиноговая оценка знаний студенТов
- •Список используемой литературы
- •Содержание
- •Н.Б. Панченко, ассистент Редактор: о.М. Барбаков, д.С.Н., профессор
- •625000, Г. Тюмень, ул. Володарского,38
- •625039, Г. Тюмень, ул. Киевская, 52
Задачи для самостоятельной и практической работы
Найти линейные комбинации заданных матриц:
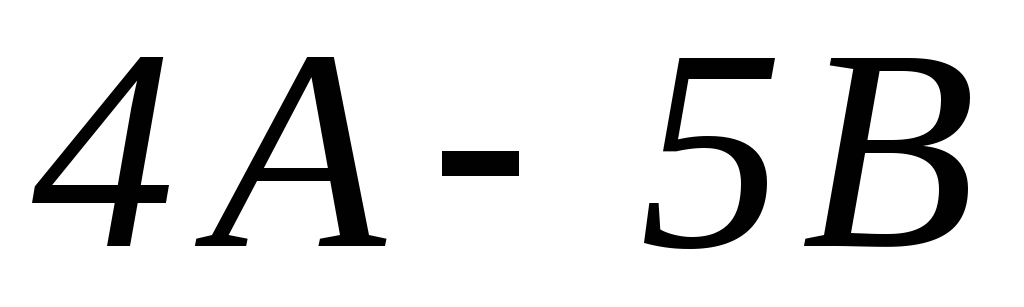 ,
где
,
где
 ,
, .
.
Ответ:
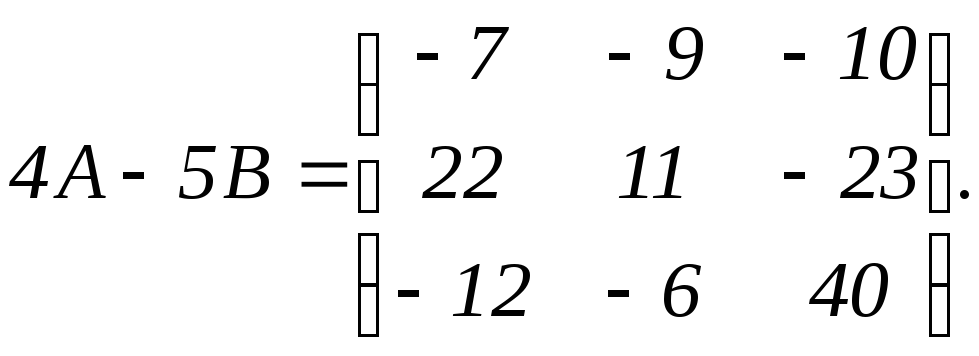
 ,
где
,
где
 ,
,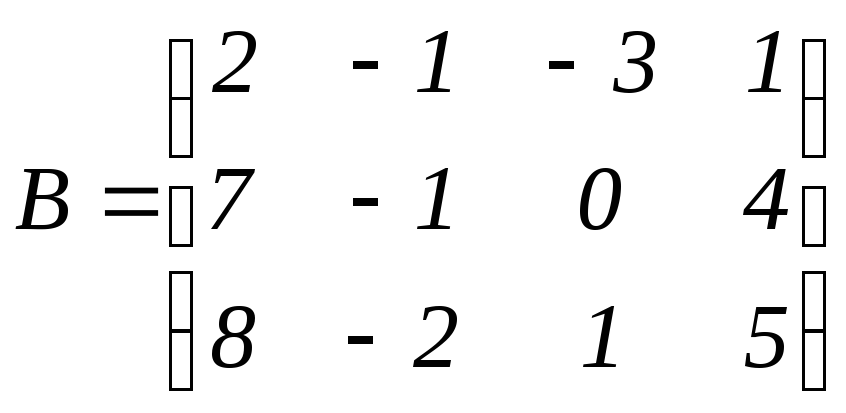 .
.
Ответ:
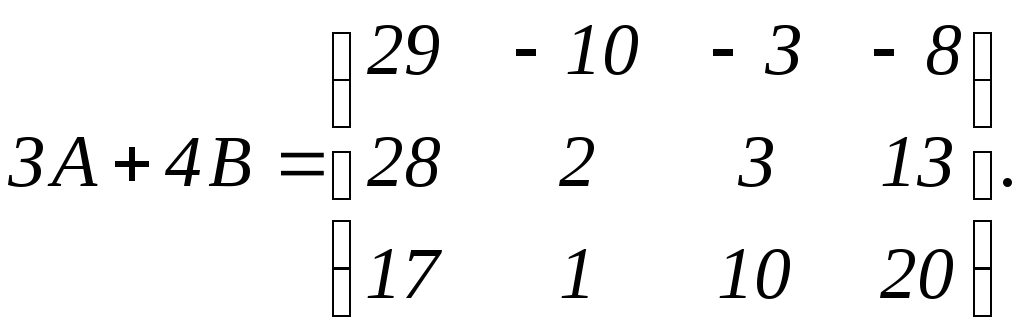
 ,
где
,
где
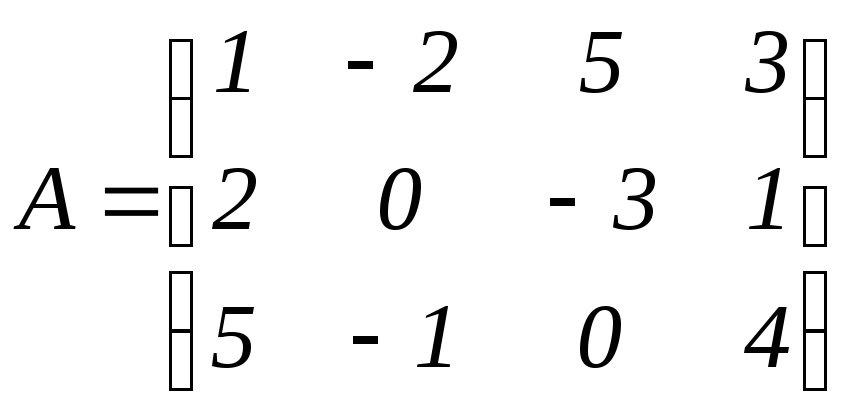 ,
, .
.
Ответ:

 ,
где
,
где
 ,
, ,
,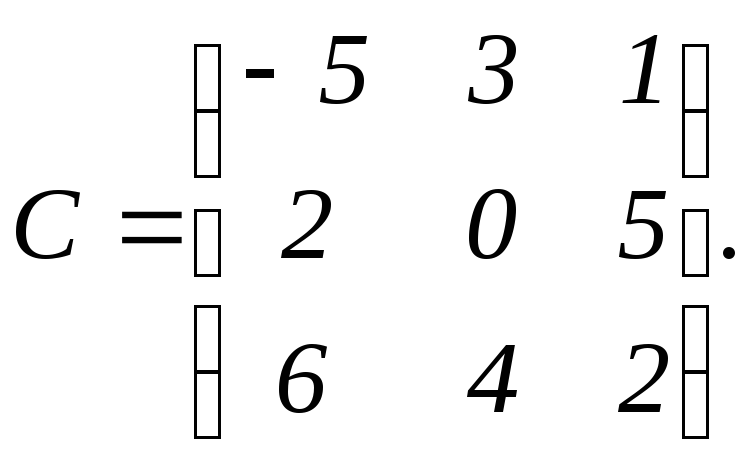
Ответ:
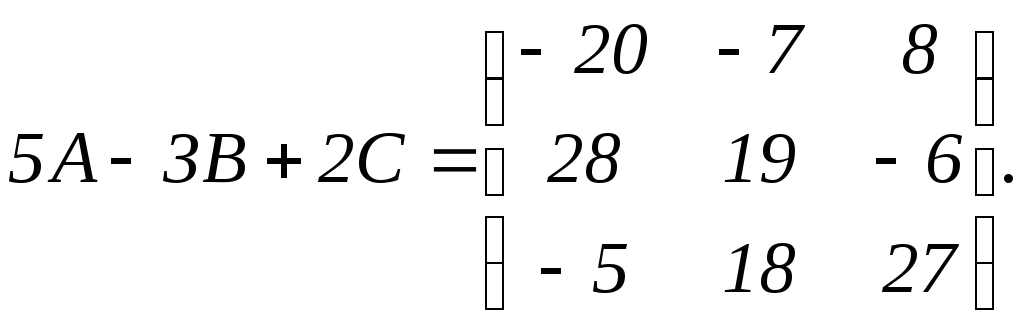
Найти произведение матриц
 и
и ,
если это возможно:
,
если это возможно: ,
,
 .
.
Ответ:
![]() ,
,
 ,
,
 .Ответ:
.Ответ:
 ,
, .
. ,
,
 .Ответ:
.Ответ:
 ,
, .
. ,
,
 .Ответ:
.Ответ:
 ,
, .
. ,
,
 .Ответ:
.Ответ:
 ,
, .
.
 .
.
Ответ:
![]() ,
,
Ответ:
 ,
, .
.
Найти произведение матриц
 и
и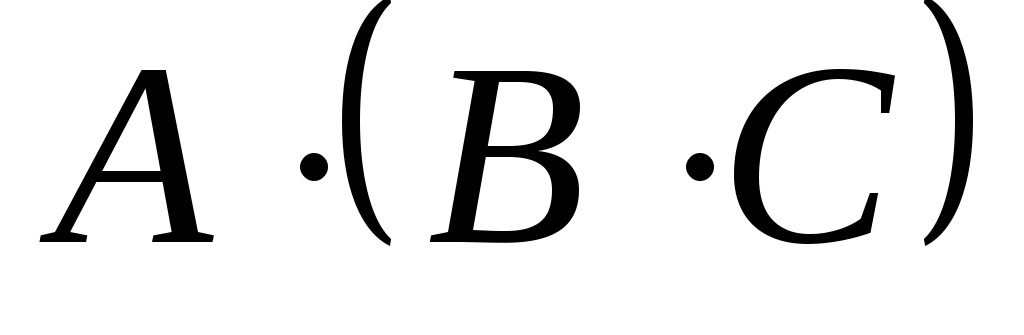 :
: ,
,
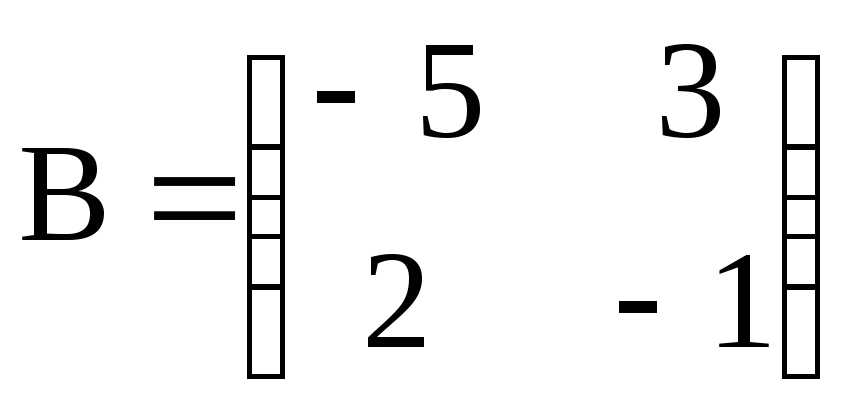 ,
, .
. ,
,
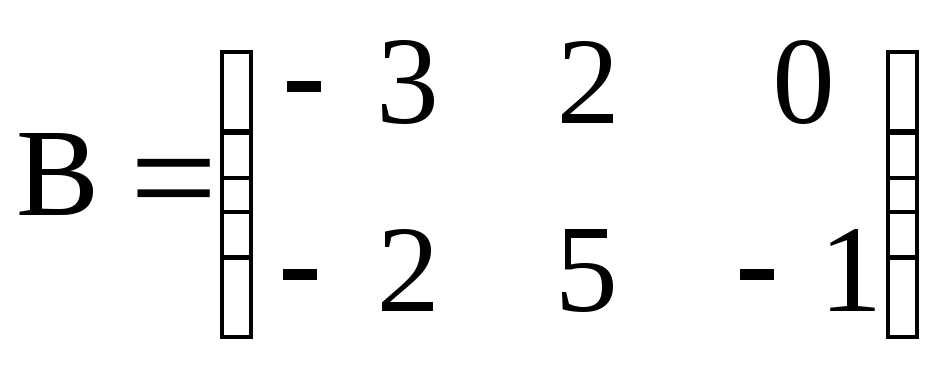 ,
, .
. ,
,
 ,
, .
.
Найти значение матричного многочлена
 ,
если:
,
если: ,
,
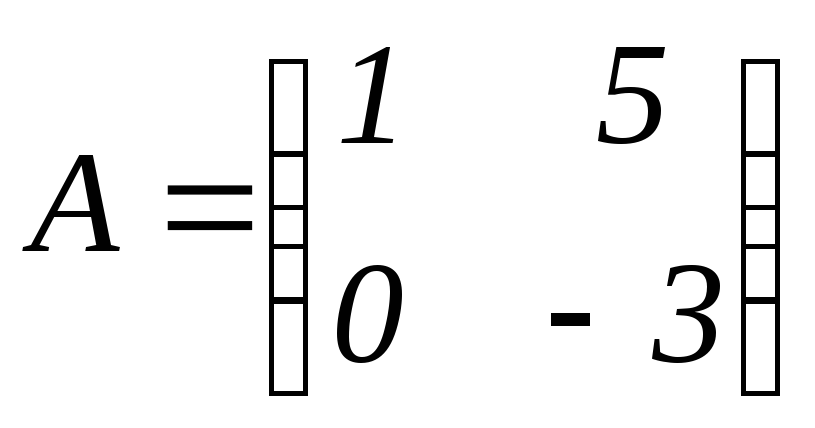 .Ответ:
.Ответ:
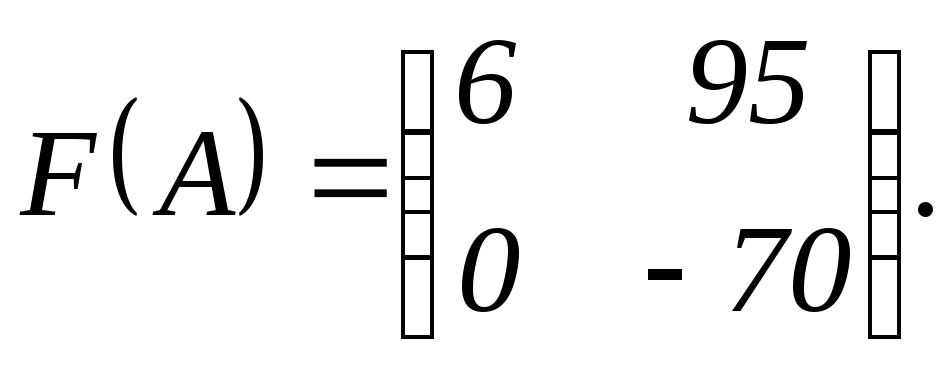
 ,
,
 .Ответ:
.Ответ:

 ,
,
 .Ответ:
.Ответ:

 ,
,
 .Ответ:
.Ответ:

 ,
,
 .Ответ:
.Ответ:
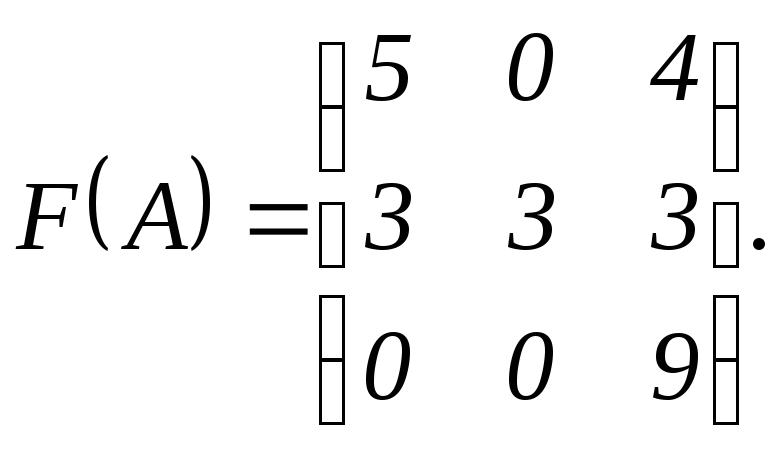
 ,
,
 .
.
Ответ:

Найти матрицу
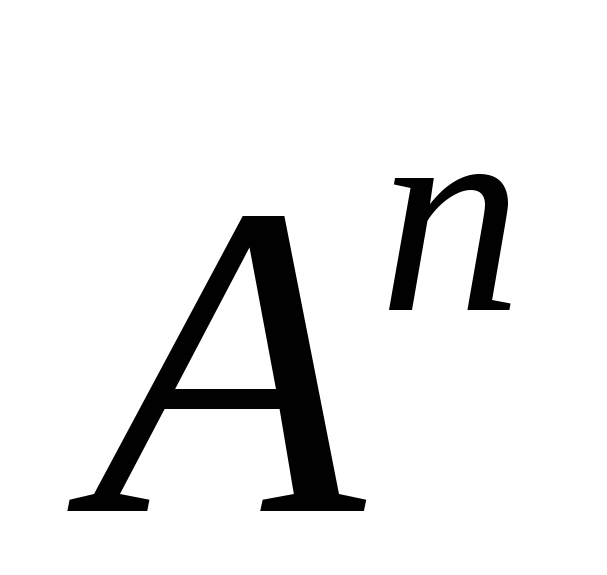 :
:
|
1)
|
2)
|
3)
|
Транспонировать матрицу:
|
|
|
Вычислить определитель:
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
Найти ранг матрицы:
 .
Ответ:
2.
.
Ответ:
2.
 .
Ответ:
3.
.
Ответ:
3.
 .
Ответ:
3.
.
Ответ:
3.
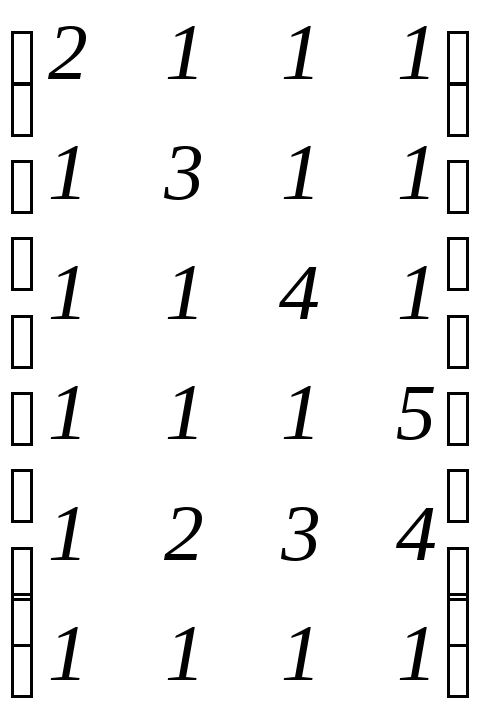 .
Ответ:
4.
.
Ответ:
4.
 .
Ответ:
2.
.
Ответ:
2.
 .
Ответ:
3.
.
Ответ:
3.
 .
Ответ:
3.
.
Ответ:
3. .
Ответ:
2.
.
Ответ:
2. .
Ответ:
2.
.
Ответ:
2.
Найти обратную матрицу:
 .
Ответ:
.
Ответ:

 .
Ответ:
.
Ответ:
 .
.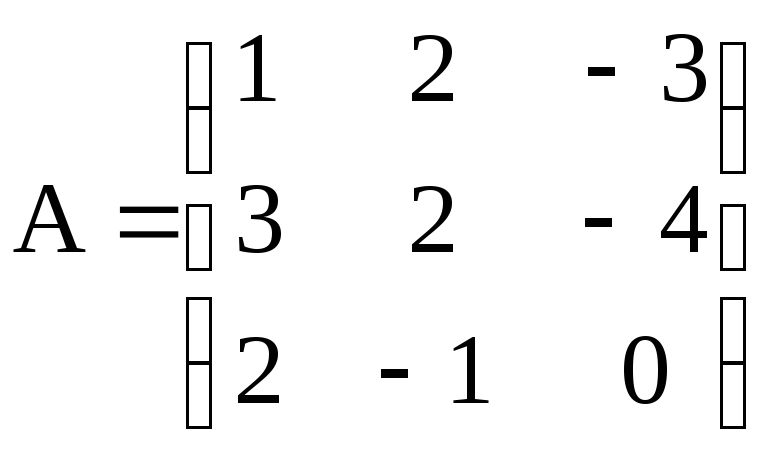 .
Ответ:
.
Ответ:
 .
. .
Ответ:
.
Ответ:
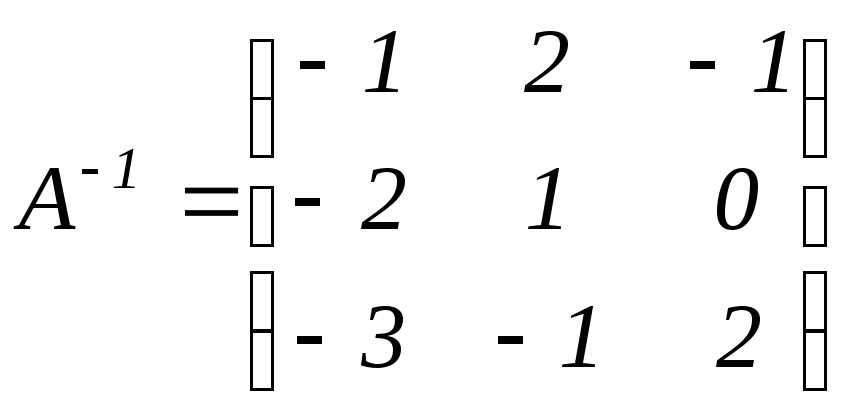 .
.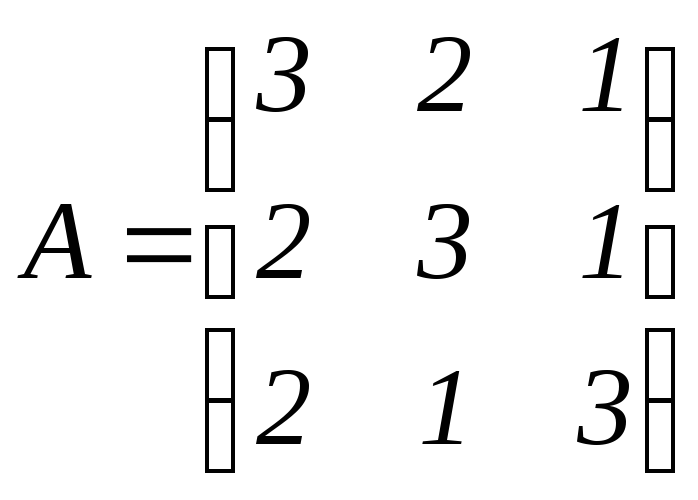 .
Ответ:
.
Ответ:

 .
Ответ:
.
Ответ:
 .
. .
Ответ:
.
Ответ:
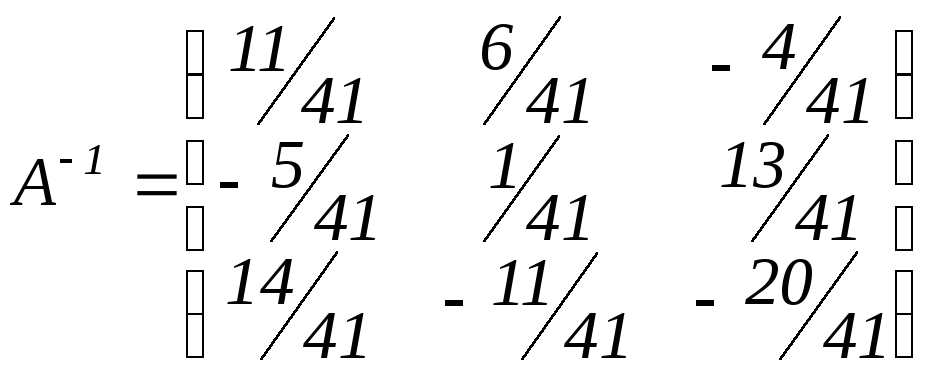 .
.
Решить матричное уравнение:
 .
Ответ:
.
Ответ:
 .
. .
Ответ:
.
Ответ:
 .
. .
Ответ:
.
Ответ:
 .
.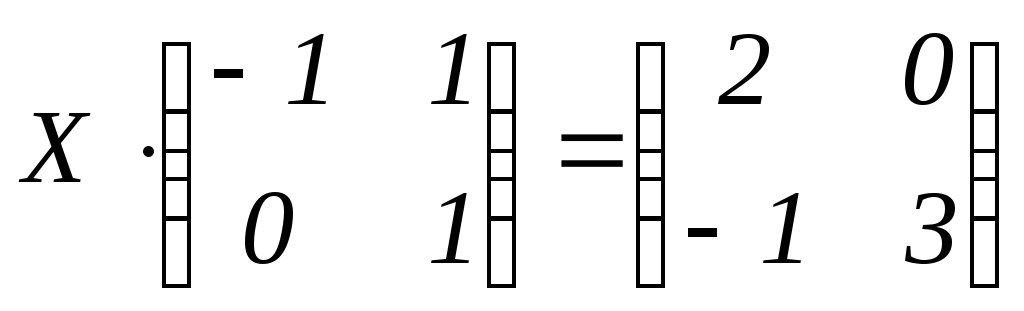 .
Ответ:
.
Ответ:
 .
. .
Ответ:
.
Ответ:
 .
. .
Ответ:
.
Ответ:
 .
. .
.
Ответ:
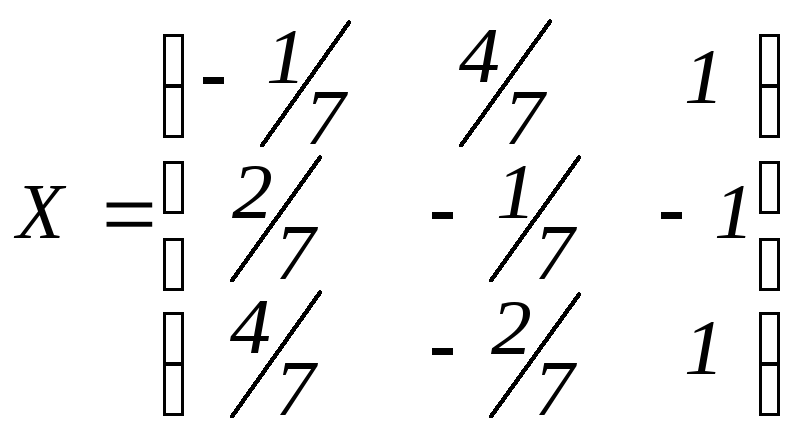 .
.
Исследовать системы линейных уравнений, для совместных систем найти общее и одно частное решение:
Ответ:
система совместна и неопределенна,
общее решение
![]() ,
частное решение
,
частное решение![]() .
.
Ответ: система несовместна.
Ответ:
система совместна и определена, о. р. -
![]() ,
ч. р. -
,
ч. р. -![]() .
.
Ответ: система несовместна.
Ответ: система несовместна.
Ответ:
система совместна и определенна, о. р.
-
![]() ,
ч.р. -
,
ч.р. -![]() .
.
Ответ:
система совместна и неопределенна,
общее решение
![]() ,
частное решение
,
частное решение![]() .
.
Ответ:
система совместна и неопределенна,
общее решение
![]() ,
частное решение
,
частное решение![]() .
.
Ответ:
система совместна и определенна, о.р. -
![]() ,
ч.р. -
,
ч.р. -![]() .
.
Ответ:
система совместна и неопределенна,
общее решение
![]() ,
частное решение
,
частное решение![]() .
.
Ответ:
система совместна и неопределенна,
общее решение
![]() ,
частное решение
,
частное решение![]() .
.
Ответ:
система совместна и определенна, о.р. -
![]() ,
ч.р. -
,
ч.р. -![]() .
.
Решить систему линейных уравнений методом обратной матрицы и по формулам Крамера:
 Ответ:
Ответ:
 .
. Ответ:
Ответ:
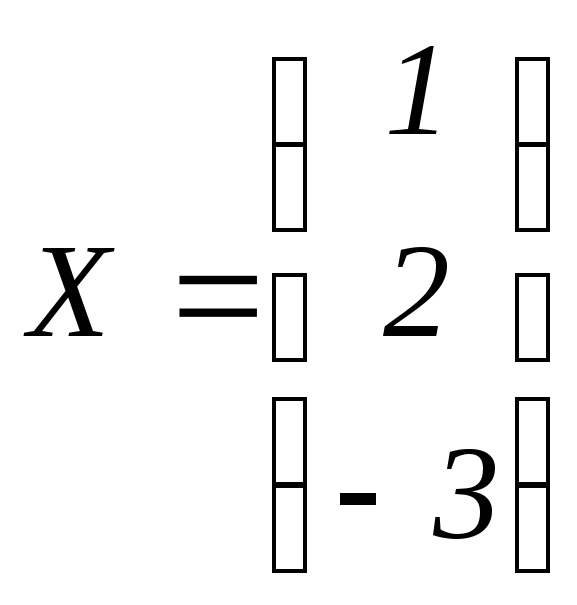 .
. Ответ:
по формулам Крамера и с помощью обратной
матрицы систему решить нельзя.
Ответ:
по формулам Крамера и с помощью обратной
матрицы систему решить нельзя. Ответ:
Ответ:
 .
. Ответ:
Ответ:
 .
. Ответ:
Ответ:
 .
. Ответ:
Ответ:
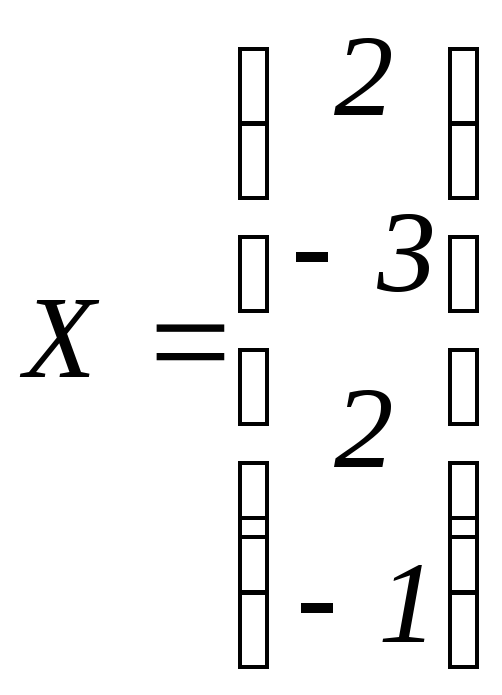 .
. Ответ:
Ответ:
 .
.Найти неизвестные коэффициенты многочлена
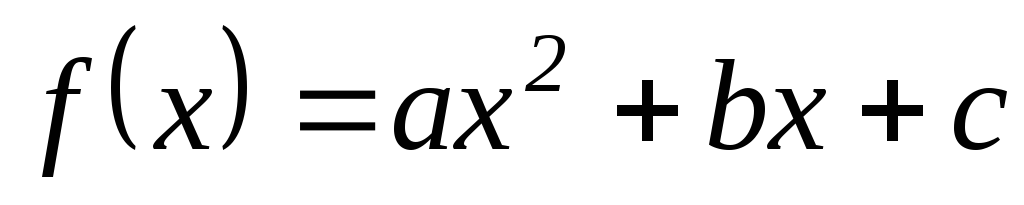 удовлетворяющего условиям:
удовлетворяющего условиям: ,
, ,
, .
.
Ответ:
![]() .
.
Найти неизвестные коэффициенты функции
 удовлетворяющего условиям:
удовлетворяющего условиям: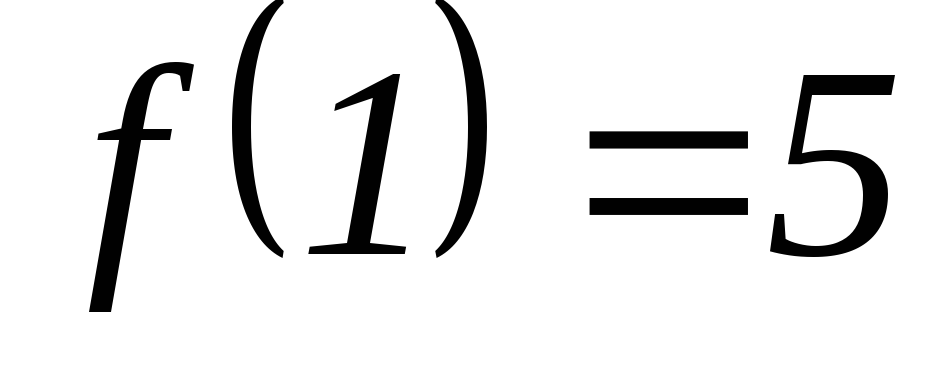 ,
,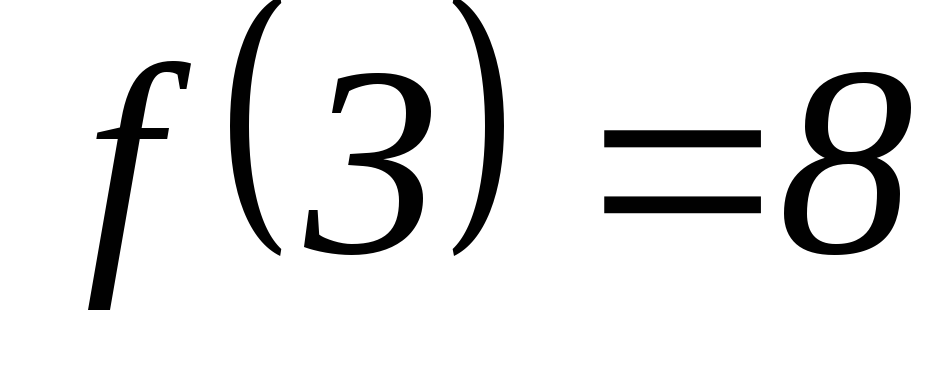 ,
, .
.
Ответ:
![]() .
.
Решить систему методом Жордана – Гаусса:
 Ответ:
Ответ:
 .
. Ответ:
Ответ:
 .
.
Пусть заданы вектора
 и
и .
Построить следующие вектора: а)
.
Построить следующие вектора: а) ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)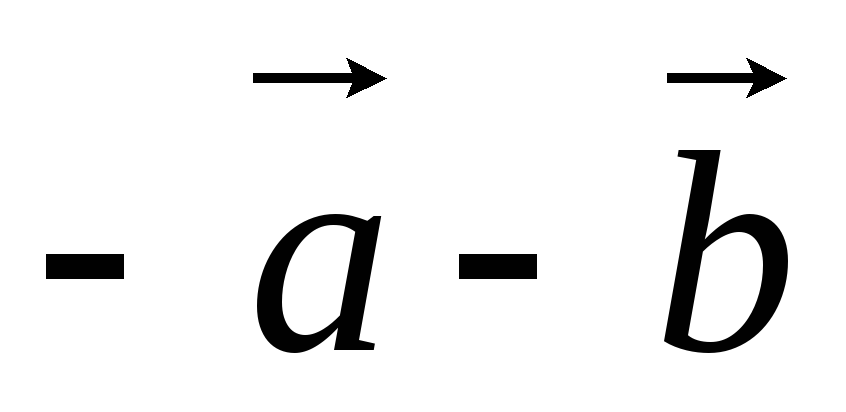 .
.Дано:
 ,
, ,
, .
Вычислить
.
Вычислить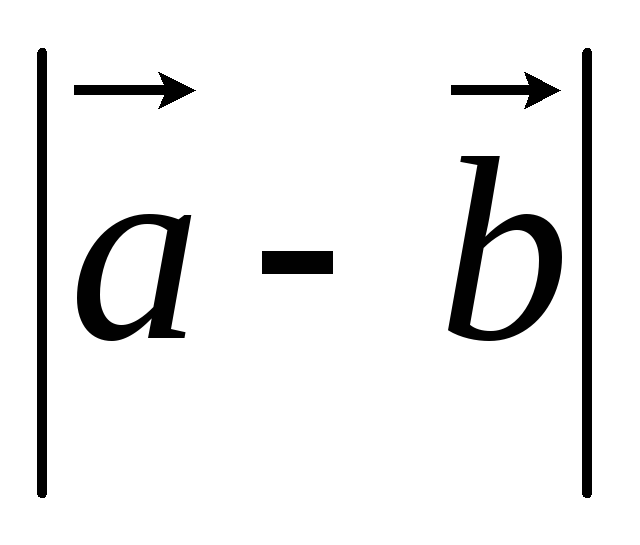 .
.В треугольнике ABC вектор
 и вектор
и вектор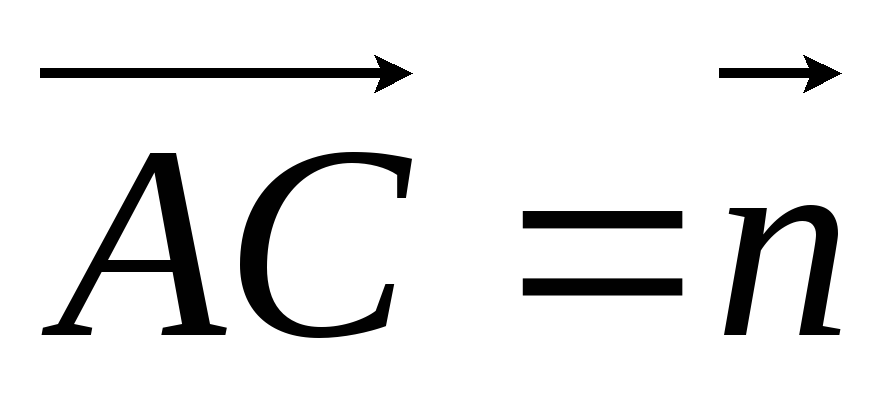 .
Построить
каждый из следующих векторов: а)
.
Построить
каждый из следующих векторов: а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г) .
.ABCDEF - правильный шестиугольник, причем
 ,
,
 .Выразить через
.Выразить через
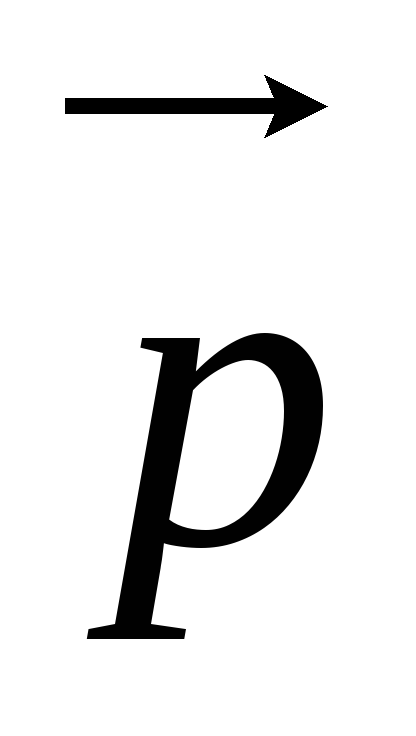 и
и
 векторы
векторы ,
, ,
, ,
,
 ,
,
 ,
, и
и
 .
.Точки К и L служат серединами сторон
 и
и
 параллелограмма
ABCD.
Выразить
векторы
параллелограмма
ABCD.
Выразить
векторы
 и
и
 через
векторы
через
векторы
 и
и .
.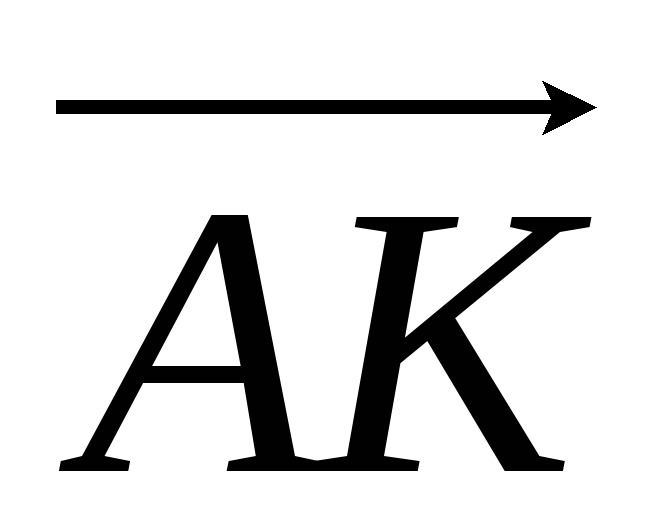 и
и
 медианы
треугольника ABC.
Выразить через
медианы
треугольника ABC.
Выразить через
 и
и
 векторы
векторы ,
, ,
, .
.
Дано разложение вектора
 по базису
по базису
 ,
, ,
, :
:
 .
Определить разложение по этому же
базису вектора
.
Определить разложение по этому же
базису вектора
 ,
параллельному вектору
,
параллельному вектору и противоположного
с ним направления, при условии, что
и противоположного
с ним направления, при условии, что
 .
.Векторы
 и
и совпадают со сторонами треугольникаABC.
Определите координаты векторов,
приложенных к вершинам треугольника
и совпадающих с его медианами AM,
BN,
СР.
совпадают со сторонами треугольникаABC.
Определите координаты векторов,
приложенных к вершинам треугольника
и совпадающих с его медианами AM,
BN,
СР.Вектор составляет с осями
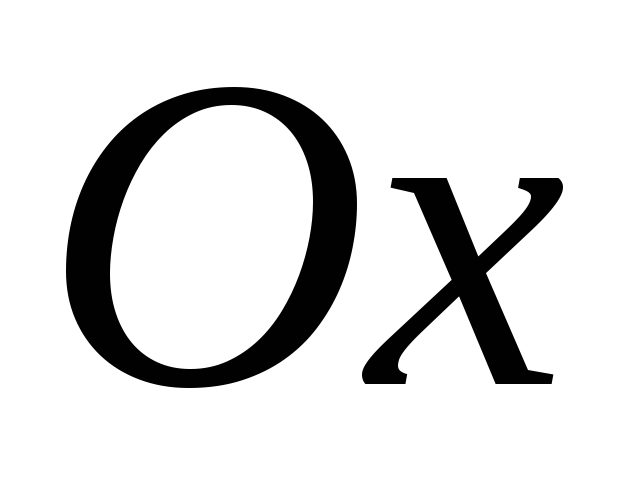 и
и
 углы
углы и
и .
Какой угол он составляет с осью
.
Какой угол он составляет с осью ?
?
Дано:
 ,
, .
Определить, при каком значении
.
Определить, при каком значении векторы
векторы и
и будут перпендикулярны.
будут перпендикулярны.Даны вершины треугольника
 ,
, ,
, .
Определить его внутренний угол при
вершине В.
.
Определить его внутренний угол при
вершине В.Даны векторы
 и
и .
Найти координаты векторных произведений:
1)
.
Найти координаты векторных произведений:
1)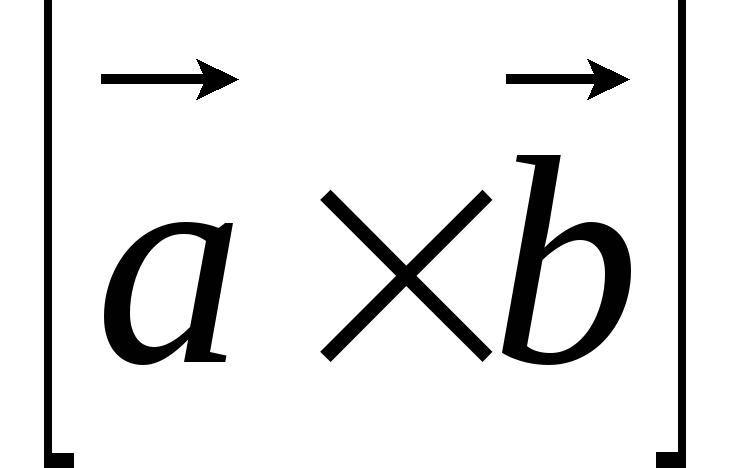 ;
2)
;
2)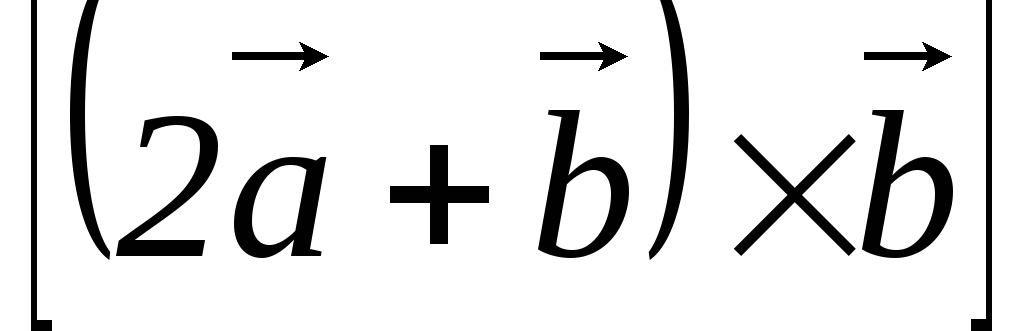 ;
3)
;
3) .
.Даны вершины треугольника
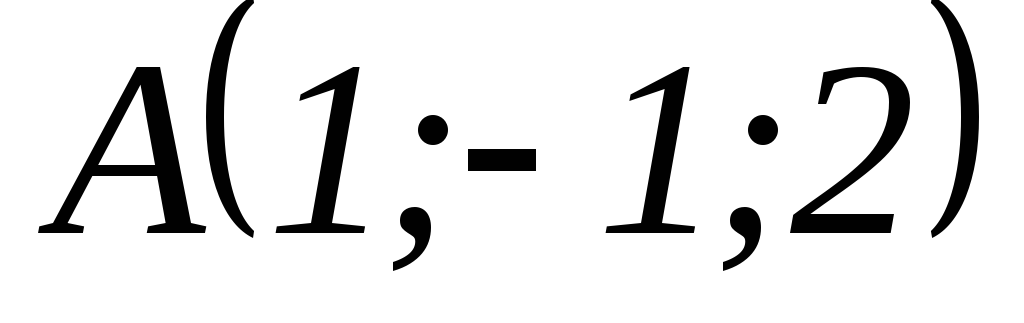 ,
, и
и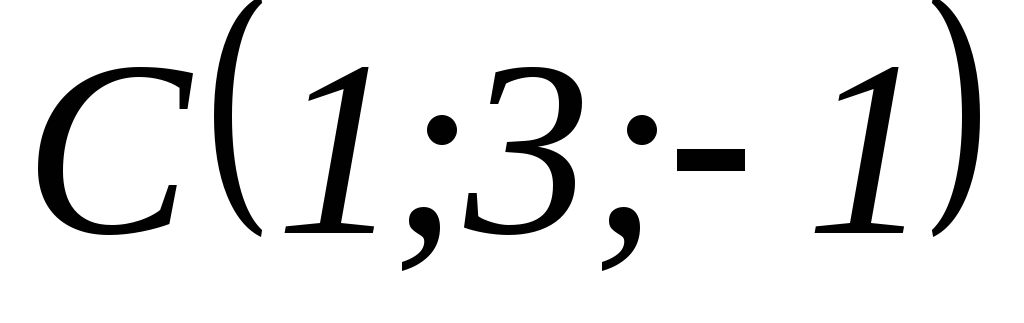 .
Вычислить длину его высоты, опущенной
из вершиныВ
на сторону
АС.
.
Вычислить длину его высоты, опущенной
из вершиныВ
на сторону
АС. Даны точки
 ,
, ,
, .
Вычислить площадь треугольникаABC.
.
Вычислить площадь треугольникаABC.
Найти смешанное произведение векторов
 ,
, и
и ,
заданных
своими координатами: 1)
,
заданных
своими координатами: 1)
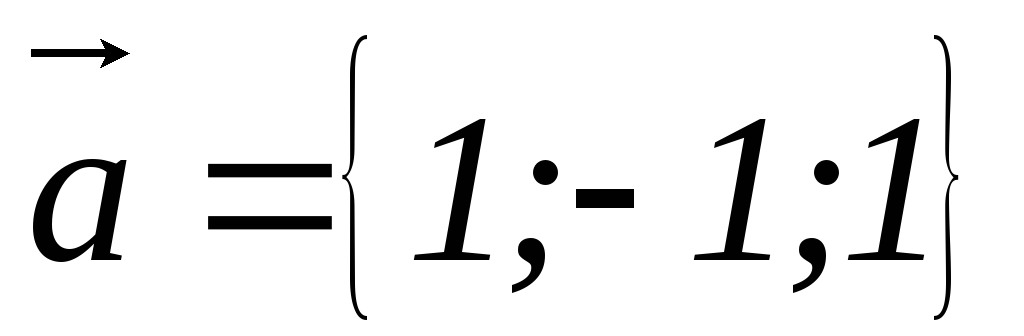 ,
, ,
,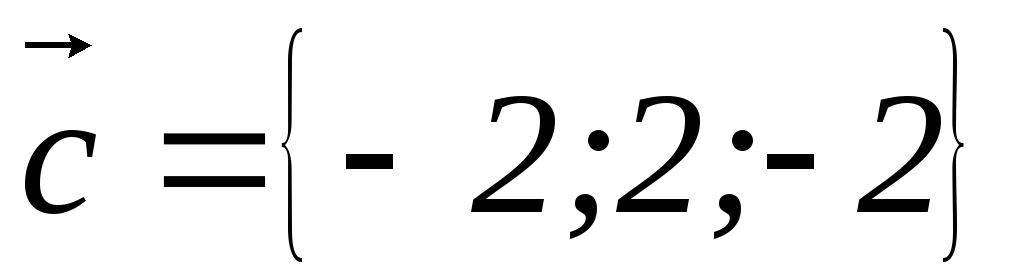 ;
2)
;
2) ,
, ,
, ;
3)
;
3)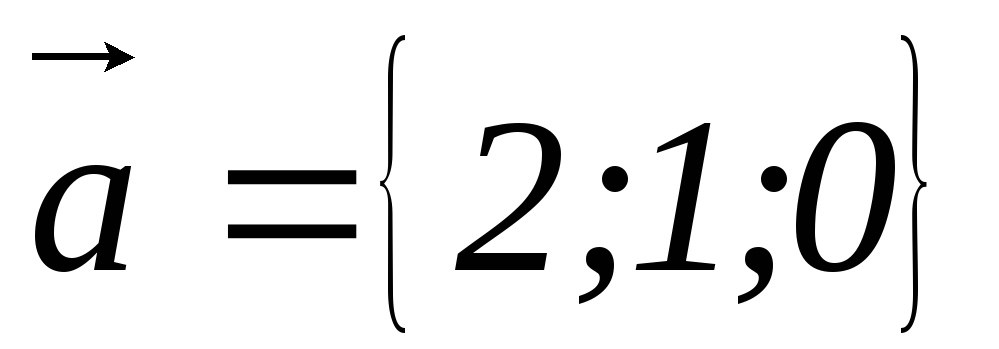 ,
, ,
,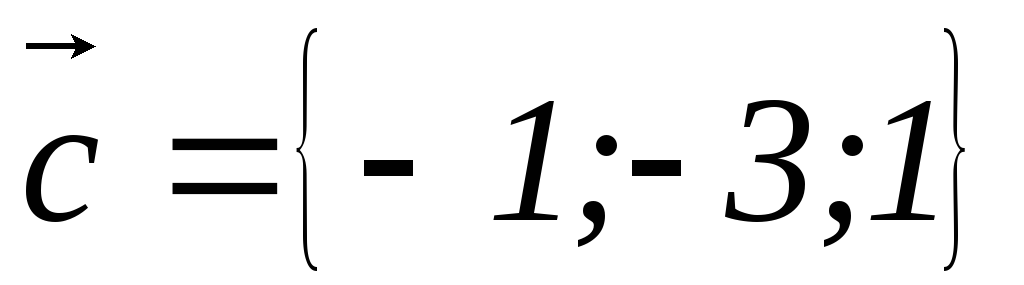 ;
4)
;
4) ,
,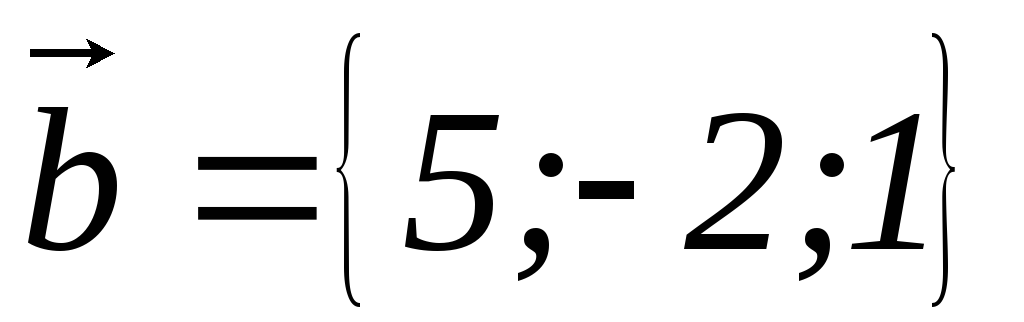 ,
, .
.Проверим, компланарны ли векторы, заданные своими координатами в произвольном базисе: а)
 ,
, ,
, ;
б)
;
б) ,
, ,
, .
.Доказать, что четыре точки
 ,
, ,
, ,
, лежат в одной плоскости.
лежат в одной плоскости.Найти длину высоты треугольной пирамиды ABCD, опущенной из вершины D на грань ABC.
 ,
, ,
, ,
, .
.Показать, что векторы
 ,
, ,
, компланарны.
компланарны.
Вычислить объем пирамиды с вершинами в точках
 ,
, ,
, ,
, .
.
Найти характеристические числа и собственные векторы линейного преобразования с матрицей
 .
.Определить характеристические числа и собственные векторы линейного преобразования с матрицей
 .
.Определить характеристические числа и собственные векторы линейного преобразования
 с матрицей
с матрицей .
.Привести к каноническому виду квадратичную форму
 .
.Привести к каноническому виду квадратичную форму
 .
.Привести к каноническому виду квадратичную форму
 .
.


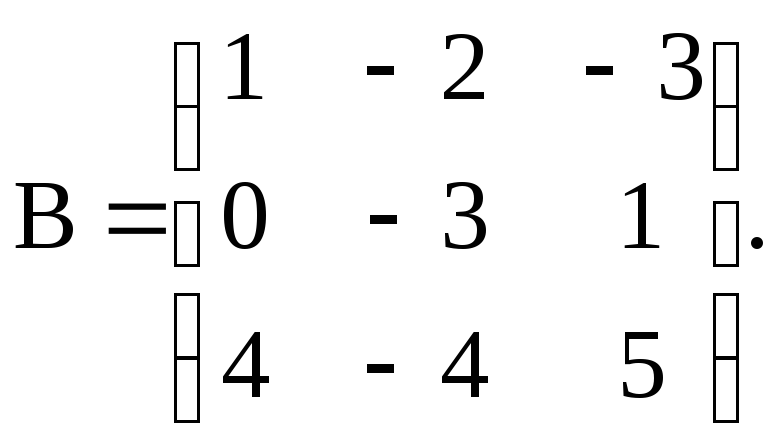
 .
. .
.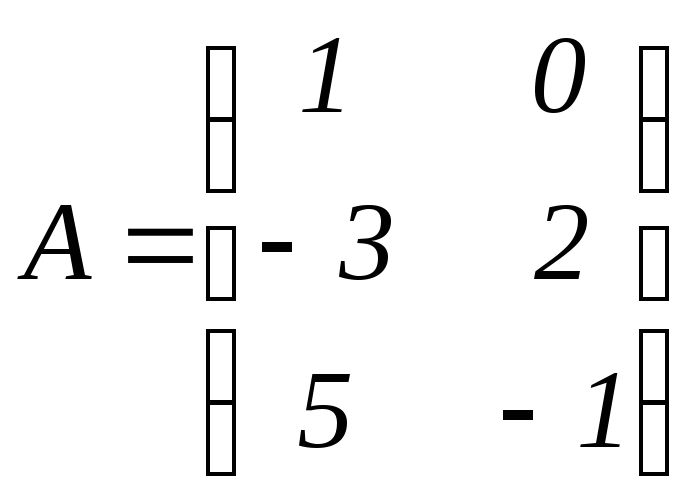 .
. .
. .
Ответ:
40.
.
Ответ:
40. .
Ответ:
-12.
.
Ответ:
-12.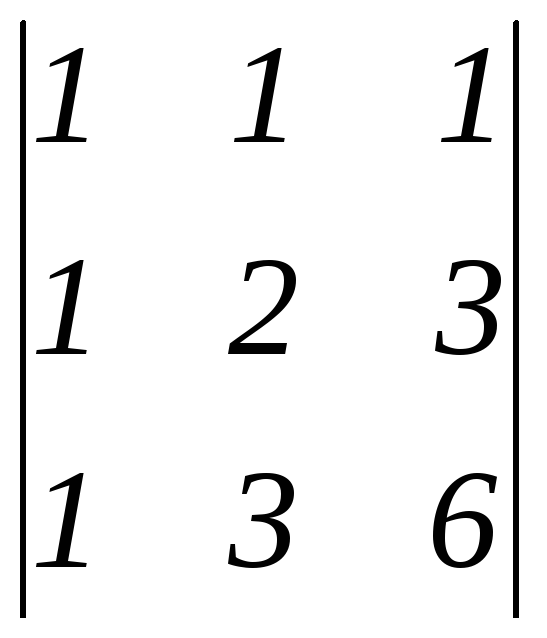 .
Ответ:
1.
.
Ответ:
1. .
Ответ:
4.
.
Ответ:
4. .
Ответ:
134.
.
Ответ:
134. .
Ответ:
.
Ответ:
 .
Ответ:
60.
.
Ответ:
60. .
Ответ:
-6.
.
Ответ:
-6. Ответ:
150.
Ответ:
150. .
Ответ:
5.
.
Ответ:
5. .
Ответ:
.
Ответ:
 .
Ответ:
52.
.
Ответ:
52.