4. Уравнения в частных производных I степени

Уравнения в частных производных I степени

1. Линейные однородные уравнения в частных производных I степени

Линейные однородные уравнения в частных производных (УЧП) I степени в общем случае имеют вид:

(1)

где - вектор независимых переменных, - вектор функций, зависящих только от , - неизвестная (искомая) функция.

Решение данного рода уравнений производится с помощью метода характеристик. Суть метода заключается в приведении УЧП I степени к системе обыкновенных дифференциальных уравнений. При этом используются первые интегралы полученной системы.

1.1 Первый интеграл системы обыкновенных дифференциальных уравнений.

Первым интегралом системы обыкновенных дифференциальных уравнений вида:

(2)

называется функция , такая что ее производная вдоль направления вектора равна нулю, т.е.:

(3) .

При этом для автономных систем (т.е. систем вида (2), где параметр не входит в правую часть уравнений) существует независимый первый интеграл.

Для нахождения первых интегралов системы (2) необходимо из ее решений (если они существуют!) последовательно исключать вспомогательную переменную .

(пример №1): задана система уравнений:

решая каждое из уравнений системы, получим:

отсюда: и первый интеграл запишется в виде: . Для проверки необходимо результат подставить в уравнение (3):

Семейство кривых уровня при представлено на рисунке 1.

Рис 1. Кривые уровня уравнения

Отсюда следует, что первый интеграл сохраняет постоянные значения вдоль направления (т.е. вдоль вектора , см уравнение (3)).

1.2 Метод характеристик

Для уравнения (1) вводится вспомогательная переменная и составляется система уравнений типа (2). Для полученной системы находятся первый интеграл. Доказано что произвольная функция (здесь ) от первых интегралов системы (2) является решением УЧП I степени (1). Решение:

(4)

является общим решением УЧП I степени (1). Это устанавливается подстановкой (4) в (1). Иначе это устанавливается тем, что уравнение (1) означает равенство нулю производной от вдоль направления вектора и то же действительно для первых интегралов (см. уравнение (3)).

Практически для решения УЧП I степени методом характеристик можно воспользоваться следующим алгоритмом:

а) записать систему (2) для уравнения (1).

б) решить систему (2), объединить решения путем исключения вспомогательной переменной и найти первый интеграл

в) записать решение (1) в виде (4).

В дальнейшем, если не оговаривается особо, для УЧП I степени порядка в качестве независимых переменных будем обозначать - координатные переменные.

(пример №2): задано УЧП I степени

(знак минус нельзя опускать при преобразовании констант интегрирования )

Объединяя решения, получим: , отсюда первый интеграл и общее решение УЧП I степени запишется в виде: , где - произвольная функция.

На рисунке 2 представлено семейство характеристик при , а также поверхности функций , и при ,

На рисунке 3 представлена поверхность функций и нанесены линии характеристик (в плоскости ). Видно, что вдоль характеристик значения функции остаются неизменными.

1

2

3

4

Рис 2. Семейство характеристик [1]; поверхности функций [2], [3] и [4].

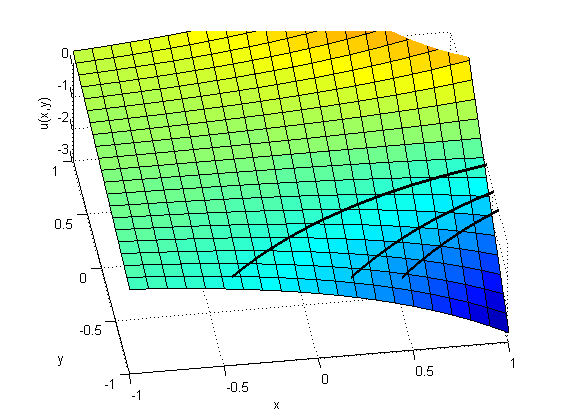
Рис 3. Поверхность функций и линии характеристик

1.3 Задача Коши

Для выделения из общего решения УЧП I степени частного решения необходимо иметь начальное условие, которое задается на гиперповерхности – поверхности, размерность которой на единицу меньше размерности исходного уравнения. Таким образом, начальное условие будет задаваться в виде:

(5)

где - обозначает гиперповерхность. Так, для уравнения гиперповерхность будет являться линией, например .

Условие (5) вместе с уравнением (1) образует задачу Коши. Доказано, что эта задача имеет однозначное решение в некоторой окрестности точки , если гиперповерхность не касается кривых характеристик (т.е. пересекает характеристики не под нулевым углом). Для нахождения частного решения (т.е. для определения функции из (4)) в этом случае достаточно подставить общее решение в условие (5).

(пример №3) решить задачу Коши для уравнения с начальным условием ().

Рис 4. Семейство характеристик и гиперповерхность

На рисунке 4 представлено семейство характеристик данного уравнения (см пример №2) и гиперповерхность . Так как гиперповерхность не касается характеристик, то можно найти частное решение УЧП. Для этого общее решение данного уравнения подставляем в начальные условия:

,

отсюда - искомое частное решение.

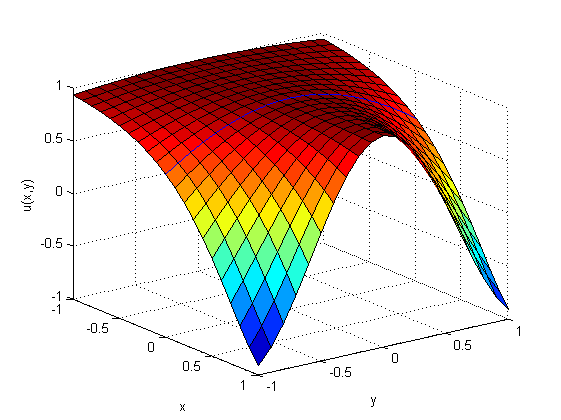
Рис 5. Поверхность функции и гиперплоскость

(синяя линия)

2. Линейные неоднородные уравнения в частных производных I степени

Неоднородное уравнение в частных производных I степени записывается в следующем виде:

(6)

где - функция от вектора переменных . Подобно решению линейных неоднородных обыкновенных дифференциальных уравнений, решение уравнений типа (6) ищется в виде суммы общего решения однородного уравнения и частного решения неоднородного. Для этого, система характеристик (2) дополняется уравнением для функции :

(7)

Система (7) представляет собой систему обыкновенных дифференциальных уравнений в расширенном пространстве. Если решение системы (2), взятое в виде функций по вспомогательным переменным подставить в (7), то последнее уравнение будет представлять собой производную функции : и его можно проинтегрировать по (вдоль характеристики), тем самым получив искомое частное решение: .

Итоговое решение уравнения (6) запишется в виде:

(8) .

Задача Коши решается (с теми же условиями наличия решения) для уравнения (6) также как и для уравнения (1).

(пример №4): задано неоднородное УЧП I степени

а) решаем систему характеристик

Объединяя решения, получим: , отсюда первый интеграл и общее решение УЧП I степени запишется в виде: .

б) находим частное решение, для чего записываем уравнение для :

Итоговое решение запишется в виде: .

На рисунке 6 представлена поверхность функций и нанесены линии характеристик (в плоскости ). Для неоднородных уравнений характерно то, что вдоль линий характеристик функция уже не сохраняет постоянные значения.

Рис. 6 Поверхность функции и линии характеристик.

3. Квазилинейные уравнения в частных производных I степени

Квазилинейные уравнения в частных производных (УЧП) I степени имеют вид:

(8) ,

где - вектор независимых переменных, и - функции зависящие от и , - неизвестная (искомая) функция.

Решение данного уравнения ищется на системе характеристик, вида:

(9) ,

где - вспомогательная переменная. Система (9) представлена в n+1 – мерном (расширенном) пространстве; для ее решения необходимо рассматривать все n+1 уравнения совместно. Напомним что для неоднородного уравнения (у которого система характеристик имеет также расширенный вид), решение находилось для n первых уравнений, затем результат подставлялся в последнее уравнение.

Таким образом, для системы (9) находятся n первых интегралов, (зависящих от и ) и общее решение уравнения (8) записывается в неявном виде:

(10) ,

т.е. выражение (10) нельзя разрешить относительно .

(пример №1): задано квазилинейное УЧП I степени

Решаем расширенную систему характеристик:

Объединяя 1-е и 3-е уравнение системы, получим: , отсюда первый интеграл: .

Далее чтобы найти интеграл во 2-м уравнении, подставим в него переменную , выраженную из 3-го уравнения: и второй первый интеграл: .

В итоге получим общее решение в неявном виде:

Задания по теме «Уравнения в частных производных I степени»

Задание №1. Найти общее решение однородных уравнений в частных производных:

а)

б)

Изобразить линии характеристик, примеры функций являющихся решениями данных уравнений.

Задание №2. Найти общее решение однородного уравнения

Изобразить линии характеристик, примеры функций являющихся решениями данных уравнений.

Решить задачу Коши для данного уравнения с начальными условиями:

а)

б)

Задание №3. Найти решение неоднородного уравнения

при начальных условиях . Изобразить поверхность функции

Задание №4. Найти общее решение квазилинейных уравнений

а)

б)

Ответы и дополнительные задания:

Ответ к заданию №1. а) ; б)

Необходимо построить поверхности этих функций, наложить на них линии характеристик и убедиться что вдоль этих линий функция неизменна.

Ответ к заданию №2 Вариантов ответов может быть множество, в зависимости от способов нахождения тригонометрических интегралов и тригонометрических постановок. Для проверки правильности решения (как и в любом примере) необходимо результат (т.е. функцию ) подставить в исходное уравнение, найти частные производные и проверить, является ли получившееся тождество верным. Так, результатом является функция , легко получаемая при использовании табличных неопределенных интегралов для секанса и косеканса. Проверка этой функции непосредственной подстановкой проблематична, поэтому проще посчитать символьно подстановку в исходное уравнение в Matlabe, затем подставить числа вместо и убедиться, что результат для широкого диапазона вариаций близок к нулю (т.е. к правой части исходного уравнения).

Далее необходимо найти частные решения при заданных гиперповерхностях и . Для этого строим линии характеристик, проекцию гиперповерхности и соотносим результаты (см. рисунок):

Можно заметить, что гиперповерхность (изображена отдельно справа) л совпадает с линией характеристики при x = 0, поэтому частное решение для может не существовать.

Ищем частное решение для, для чего подставляем его в общее:

заменяем: , отсюда: и и окончательно:

Ответ к заданию №3.

Необходимо построить поверхность этой функции, гиперповерхность и убедится что поверхность проходит через гиперповерхность.

Ответ к заданию №4. а) , б)