
Формулы преобразования произведения тригонометрических функций
|
= |
cos(α - β) - cos(α + β) |
|
2 |
|
= |
sin(α - β) + sin(α + β) |
|
2 |
|
= |
cos(α - β) + cos(α + β) |
|
2 |
Формулы приведения

sin(-x) = - sinxarcsin(-x) = -arcsinx
cos(-x) = cosx arcos(-x) = π-arccosx
tg(-x) = -tgxarctg(-x) = -arctgx
ctg(-x) = -ctgxarcctg(-x) = π-arcctgx
формула дополнительного угла
asinα
+ bcosα
=
 где
где
sin =
=
 ;cos
;cos =
=

Значения тригонометрических функций


sinα
=
 cosα
=
cosα
=
 tgα
=
tgα
=
 ctgα
=
ctgα
=

Арккосинус, арксинус, арктангенс
arcsin(x) =

arccos(x) =
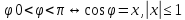 ;
;arctg(x) =
 ;
;arcctg(x) =

sin(arcsinx)=x
cos(arccosx)=x
tg(arctgx)=x
ctg(arcctgx)=x
Последовательность чисел
Арифметикалық прогрессия(an)
a1 –первый член ,…., an – n–й член,d=an+1-an=…=-разность прогрессии.
an = a1+(n-1)d. (формула n – го члена)
an =
 ,
(n>k);
,
(n>k);an = ak+(n-k)d;
 или
или (формула
суммы перых n
членов(an))
(формула
суммы перых n
членов(an))
Геометрическая прогрессия (bn)
b1
–первыйй член ,…., bn
– n
ый член, d= =…=
- знаменатель прогрессии.
=…=
- знаменатель прогрессии.
bn = b1
 q
n-1, (формула n – го члена)
q
n-1, (формула n – го члена)bn =
 ;
; =
= ;
;
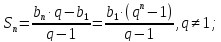
Сумма
бесонечно убывающей геометрической
прогресси при
( <1).
<1).
 ;
;
Логарифм
Логарифм числа. Свойства логарифмов
logab
 ax=
b; a logab = b, a>0, a
ax=
b; a logab = b, a>0, a
log a(bc) = logab + logac;
log a(b/c) = logab – logac;
loga(bc) = c logab;
log(ac)b = (1/c) logab;
logaa=1;
loga
 =
= ;
;logab =
 ;
;loga1=0;
logambm = logab;
 =
=
 ;
;logab=

ПРОИЗВОДНАЯ
Производная некоторых функций
C’ =0, Cϵ R
(xn)’ = nxn-1, n ϵ Z
 =
=



7.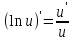
8.

9.
(

10.
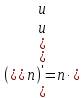
11.

12.

13.
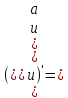
14.

15.

16.
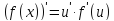
17.

Уравнение касательной к графику y = f(x)

Tg =
= -угловой
коэффициент
-угловой
коэффициент
Уравнение касательной определяется по формуле:

 –точка
пересечения (касания);
–точка
пересечения (касания);
Промежутки возрастания и убывания заданной функции
Пусть
функция y
= f(x)
непрерывна, определена и дифференцируема
на промежутке Х и равенство
 (х)=0
выполняется для конечных чисел точек
данного промежутка.
(х)=0
выполняется для конечных чисел точек
данного промежутка.
Решение неравенства
 показывает
промежуток возрастания функции.
показывает
промежуток возрастания функции.Решение неравенства
 показывает промежуток убывания функции.
показывает промежуток убывания функции.
Наибольшее и наименьшее значения непрерывной функцией y = f(x) в промежутке [a;b]:
Находится
 .
.Находим критическое точки решая уравнение
 .
.Выясняем, принадлежит ли полученные критические точки промежутку [a;b].
Находим значения функции y = f(x) на концах отрезка [a;b]
Сравнивая полученные значения функции, определяем наибольшее и неименьшее значения.
ИНТЕГРАЛ
Неопределенный интеграл

Интегральные исчисления
Методы интегрирования
Метод замены переменных

Интегрирование по частям

Определенный интеграл

Применение определенного интеграла
для вычисления площади
а)
Если

[a,b],
то
A=

б)
Если

[a,b],
то
A=-

в)
A=

г) Площадь кривой трапеций, ограниченной двумя линиями:

Применение интеграла для вычисления объемов тел вращения
Объем тела, полученного в результате вращения графика функции y=f(x), ограниченной линиями x=a и x=bвокруг оси Ох вычисляется по формуле:
V=
Объем тела, полученного в результате вращения графика функции y=f(x), ограниченной линиями y=cи y=dвокруг оси Оу вычисляется по формуле:
V=

Длина кривойy=f(x)в отрезке [a,b]


ГЕОМЕТРИЯ
ПЛАНИМЕТРИЯ
Теорема Фалеса


Основные свойства призвольного труегольника


Стороны: BC=a, AC=b,AB=c.
Периметр:P=a+b+c
Полупериметр:
Против большой стороны лежит больший угол.
Теорема косинусов:
 ;
;
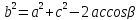 ;
;
 ;
;

Высоты:
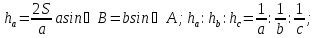
Медианы:
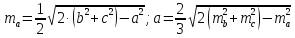
G – центр тяжести



Биссектрисы:


Пересечение биссектрис есть центр вписанной окружности.


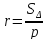



R,r – радиусы описанной и вписанной окружностей
Площадь произвольного треугольника



 ;
;
Равносторонний треугольник

h=m=l=


Прямоугольный треугольник



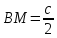

Частные случаи:

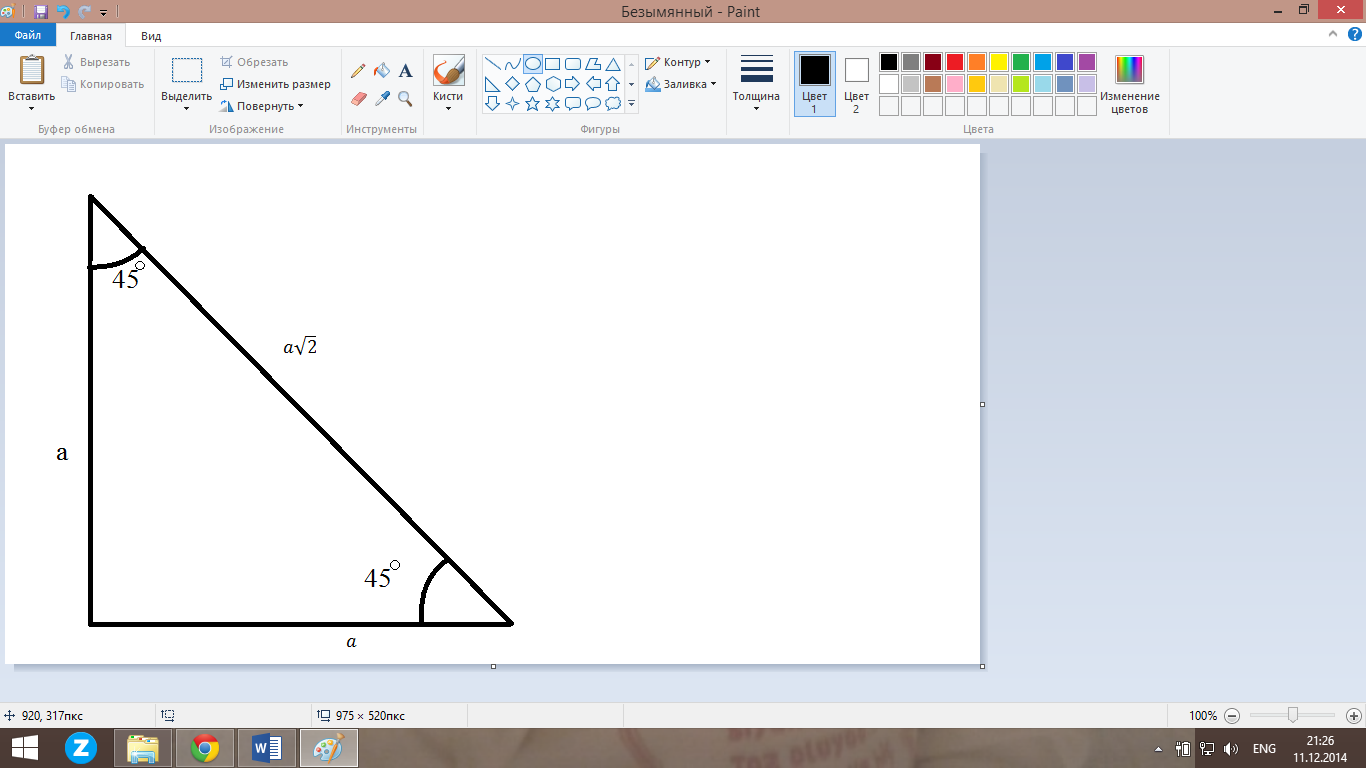
Равнобедренный треугольник

AC=BC
AH=HB

Выпуклый многоугольник
Пусть n–число сторон многоугольника.
Сумма внутренних углов многоугольника:
(n
– 2) ;
;
Сумма диагоналей:
 ;
;
Площадь правильного мнгоугольника:
S
=

где а – сторона правильного многоугольника.
Произвольный выпуклый четырехугольный

 ;
;
 ;
;
Параллелограм

 ;
;
 ;
;
 ;
;
Прямоугольник

P=2a+2b;
S=ab= ;
;
Ромб

P=4a;
S=ah= ;
;
AG= ;
;
4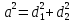 .
.
Квадрат
Диагональ: ;
;
Площадь: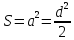 ;
;
Трапеция

AM=MD, CN=NB
m= ,
,
S=
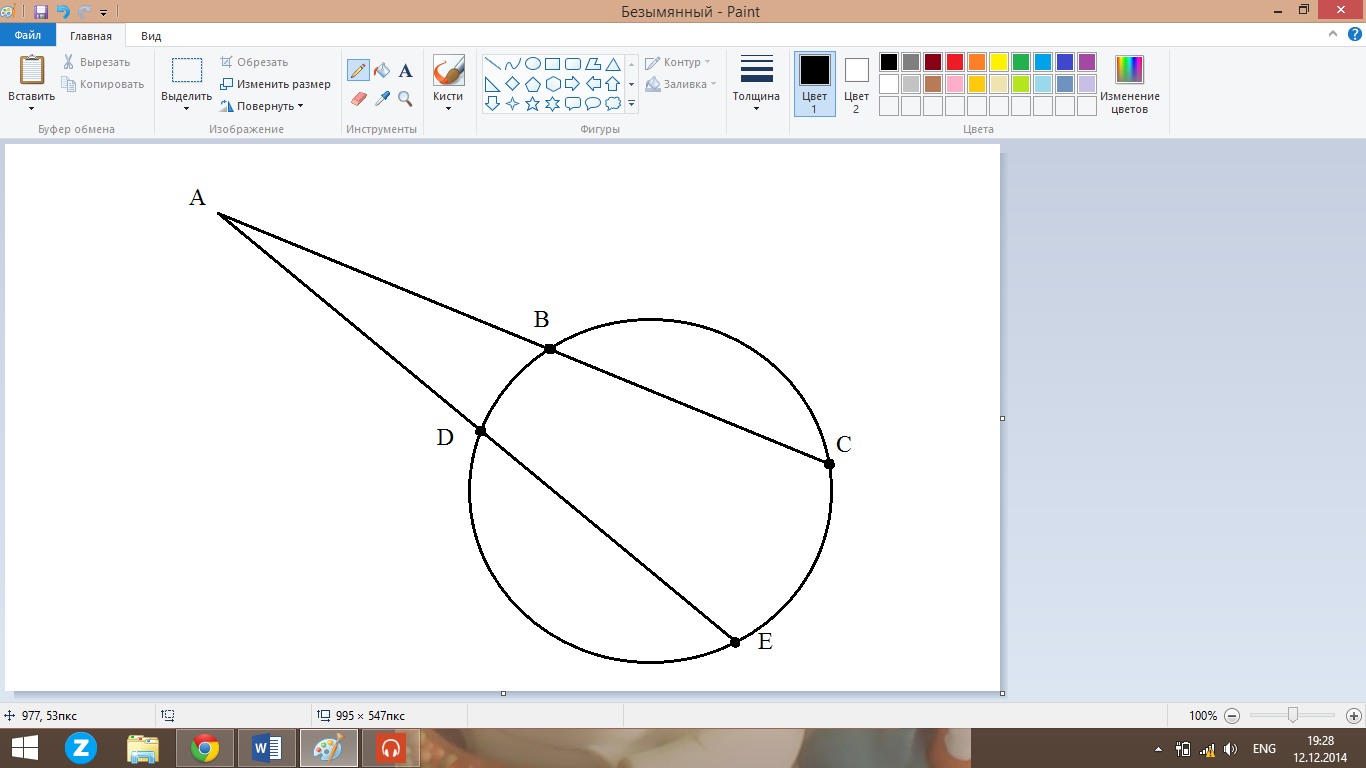
Окружность. Круг. Сектор. Кольцо

O – центр окружности
MN – диаметр окружности
AB – хорда окружности
d – диаметр окружности
r- радиус окружности
RK - секущая окружности
TQ – касательная окружности



Длина
хорды: l=2rsin

ab=cd

AC=BC

A
AB
Площадь
круга:S=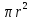
Длина
окружности:C=2
Длина
дуги: l= , где
, где
 - центральный угол
- центральный угол
Площадь
сектора:
Площадь
сегмента: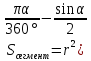 )
)
Площадь
кольцо:
СТЕРЕОМЕТРИЯ
Призма


Площадь поверхности и объем призмы
|
|
Наклонная призма |
Прямая призма |
|
Боковая поверх. |
где
перпенд.сеч, l- длина бок.ребра |
где
осн, Н - высота |
|
Полная поверх. |
|
|
|
Объем |
V= Где
|
V= Где
призмы,Н - высота |
Параллелепипед

Прямой параллелипепипед
Боковое ребра перпендикулярны основанию
Боковое грани – прямоугольники
Основания – параллелограммы

Прямоугольный параллелепипед
Все диагонали равны


V=abc

Куб
Объем
куба: V= ,где
а – длина ребра.
,где
а – длина ребра.
Полная
поверхность:S=6
Диагональ:d=a
Пирамида
 -
двугранный угол при основании
-
двугранный угол при основании
 -
угол наклона ребра к плоскости основания
-
угол наклона ребра к плоскости основания
 -
двугранный угол при боковым ребре
-
двугранный угол при боковым ребре
 −высота
−высота
l - боковое
m - апофема
r,R – радиусы вписанной в основание и описанной около основания окружностей соответственно.

Площадь поверхности и объем
произвольной пирамиды
Полная
поверхность:
Объем:
Для
правильный пирамиды
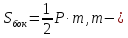 апофема.
апофема.
Тетраэдр

где а – сторона тетраэдра;R,r – радиусы описанной около тетраэдра и вписанной в тетраэдр сфер соответственно.
Усеченная пирамида

Площадь поверхности и объем усеченной пирамиды
Для
правильной усеченной пирамиды: ,
где
,
где
 периметры
оснований,
периметры
оснований, -
апофема
-
апофема
Полная
поверхность:
 +
+
Объем:
Если
 высота
меньшей пирамиды, а
высота
меньшей пирамиды, а большей,
то
большей,
то
 .
.

Цилиндр


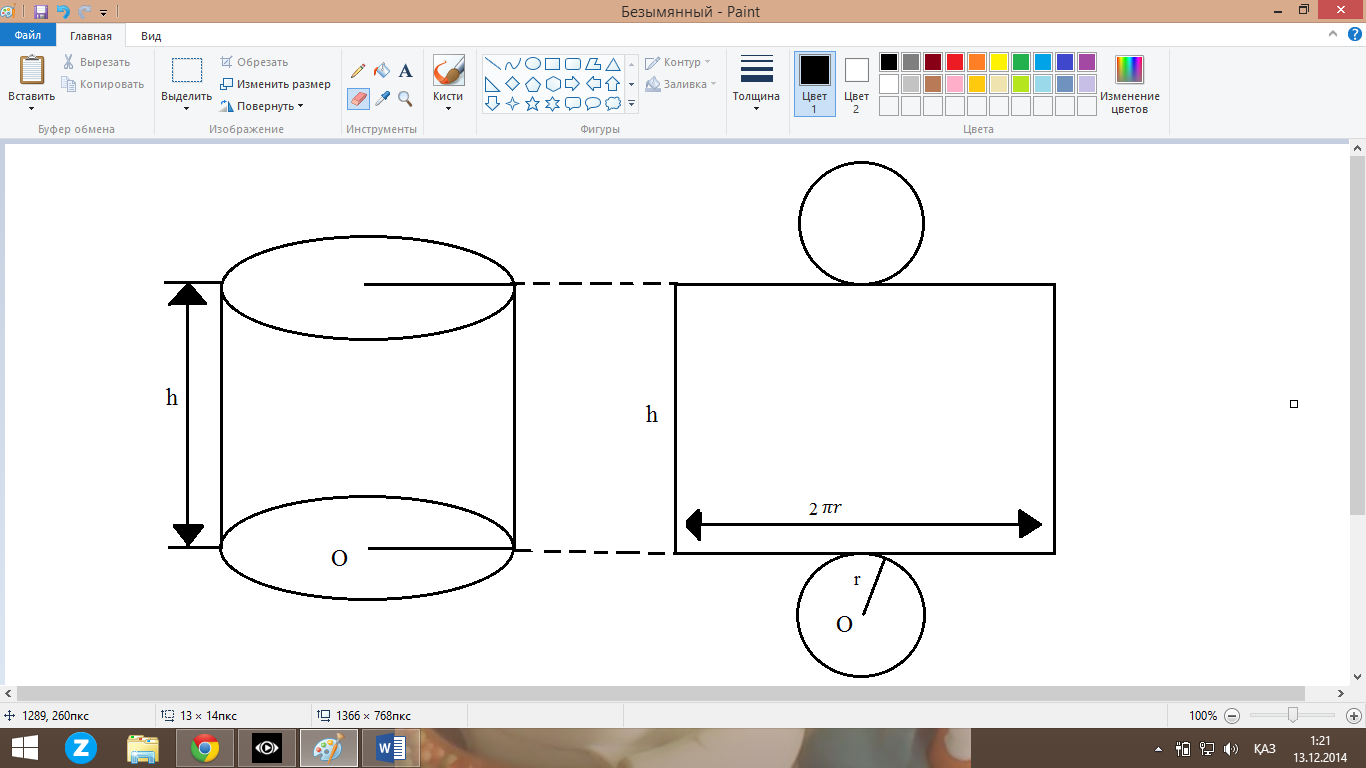
Боковая
поверхность:
 .
.
Полная
поверхность: =
=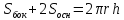 +
+ =
=
Объем
цилиндра:V= h=
h=
Конус. Усеченный конус
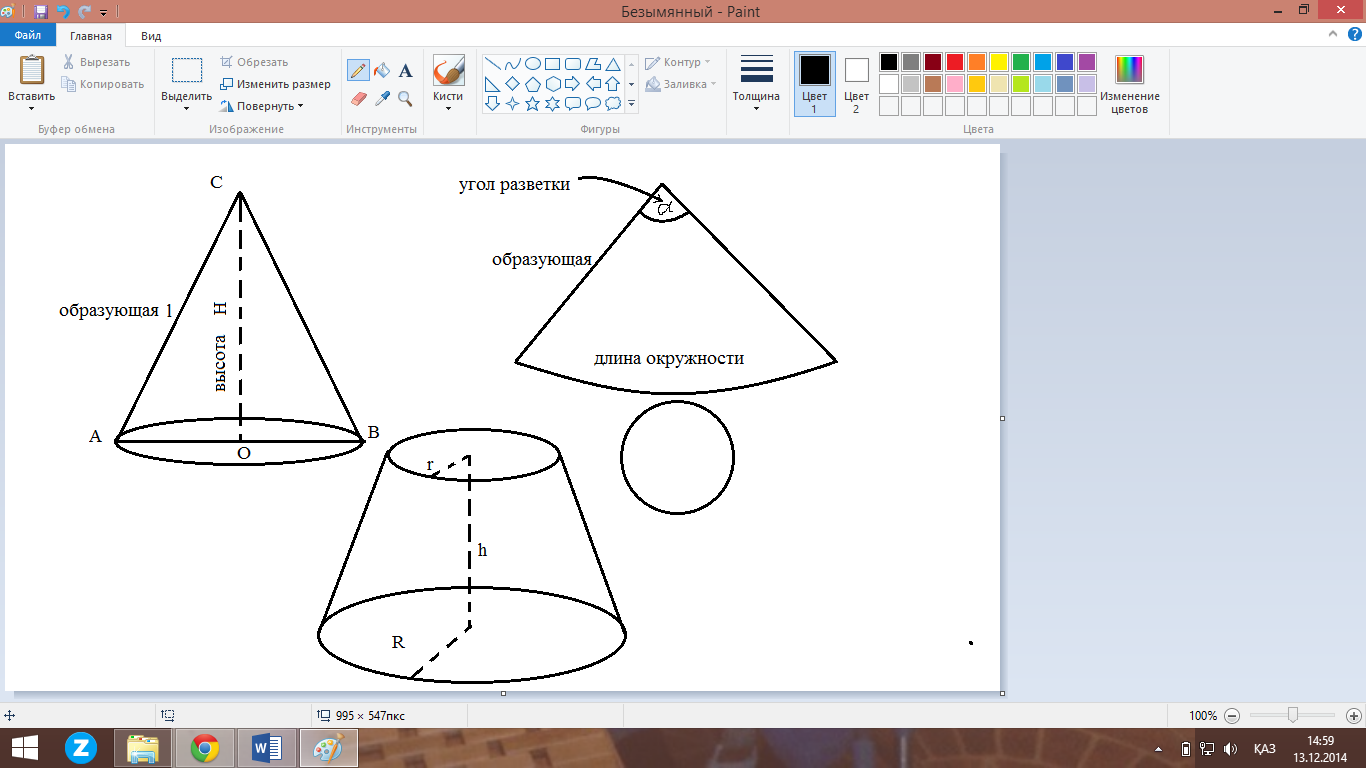
Площадь поверхности и объем конуса
|
|
Конус |
Усеченный конус |
|
Боковая поверх. |
|
L – образующая усеч.конуса |
|
Полная поверх. |
|
|
|
Объем |
|
|
Угол
развертки конуса:
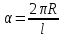
Шар. Сфера
Если
расстояние секущей плоскости от центра
шара равно d,
то r= .
.
Площадь
сферы: S=4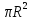
Oбъем
шара:


Части шара

|
Площадь
сегментной поверхности:
|
Площадь
полной поверхности: |
Площадь
боковой поверхности:
|
|
Объем: |
Объем:
|
Объем: |
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
На плоскости
Расстояние от точки
 )
до
начала координат:
)
до
начала координат:
Расстояние между
 )и
)и ):
):

Точка С,которая является серединой отрезка АВ, где A
 )и
B
)и
B ),
имеет
координаты
(
),
имеет
координаты
(
Точка D, которая делит отрезок АВ в отношении

 =
=
Уравнение прямой, проходящей через две заданные несовпадающие точки
 )
и
)
и ):
):
 =
=
Расстояние от точки A(
 до
прямой ax+by+c=0
находится
по формуле:
до
прямой ax+by+c=0
находится
по формуле:
d=
Пусть
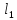 :y=
:y= и
и :y=
:y=
Если
 и
и ,
то
прямое совпадают;
,
то
прямое совпадают;Если
 но
но ,
то
прямые параллельны;
,
то
прямые параллельны;Если
 ,
то
прямые пересекаются;
,
то
прямые пересекаются;Если
 то
прямые перпендикулярны.
то
прямые перпендикулярны.



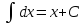





















 =
=
 =
=
 ,
, -перпенд.сеч
-перпенд.сеч .
. ,
, -осн.
-осн.
 где
где



 ,
где
,
где –площади
оснований
–площади
оснований
 .
.


